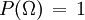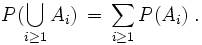Wahrscheinlichkeitsmass

In der Wahrscheinlichkeitstheorie dient ein Wahrscheinlichkeitsmaß zur mathematischen Beschreibung einer Wahrscheinlichkeitsverteilung. Ein Wahrscheinlichkeitsmaß ist eine Funktion P, die jedem Ereignis A eine Wahrscheinlichkeit P(A), also eine Zahl zwischen 0 und 1 zuordnet und folgende Eigenschaften hat:

• Normierung: Die Ergebnismenge Ω hat Wahrscheinlichkeit 1:

$P(\Omega) \, = \, 1$

• σ-Additivität: Die Wahrscheinlichkeit, dass eines von mehreren sich einander ausschließenden Ereignissen eintritt, ist die Summe der einzelnen Wahrscheinlichkeiten: Für jede Folge von paarweise disjunkten Ereignissen 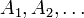$A_1,A_2, \dots$ gilt

$P(\bigcup_{i\ge1} A_i) \, = \, \sum_{i\ge1} P(A_i) \;.$

Mathematisch gesehen ist ein Wahrscheinlichkeitsmaß ein Maß P auf einem Messraum (Ω,Σ) mit der Eigenschaft P(Ω) = 1. Die Kombination von Ergebnismenge, Ereignisraum und Wahrscheinlichkeitsmaß, d. h. den Maßraum (Ω,Σ,P), bezeichnet man als Wahrscheinlichkeitsraum.