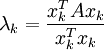Wielandt-Iteration

Die inverse Iteration ist ein numerisches Verfahren zur Berechnung von Eigenwerten von Matrizen. Sie ist eine Variante der von-Mises-Iteration, mit deren Hilfe allerdings beliebige Eigenwerte berechnet werden können. Das Verfahren wurde 1944 von Helmut Wielandt bei der Stabilitätsanalyse von Strukturen, die kleine Störungen bekannter Systeme sind, eingeführt. In diesem Fall sind gute Approximationen für die relevanten Eigenwerte bekannt, und man erhält rasche Konvergenz.

Beschreibung

Ist λ ein Eigenwert von A und x der zugehörige Eigenvektor, so ist λ − θ ein Eigenwert von (A − θI) zum Eigenvektor x, wobei I die Einheitsmatrix ist. Des Weiteren ist dann 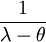$\frac{1}{\lambda-\theta}$ ein Eigenwert von (A − θI) ^{− 1} zum Eigenvektor x. Ist λ nun der Eigenwert von A, der θ am nächsten liegt, so ist 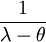$\frac{1}{\lambda-\theta}$ der betragsmäßig größte Eigenwert von (A − θI) ^{− 1}. Wendet man nun auf (A − θI) ^{− 1} die Potenzmethode an, so konvergiert x_k gegen den Eigenvektor zum Eigenwert λ von A, der θ am nächsten liegt.

Algorithmus

Gegeben sei eine quadratische Matrix 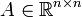$A\in\mathbb{R}^{n\times n}$, ein Startvektor 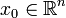$x_0\in\mathbb{R}^n$ und ein Shift 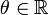$\theta\in\mathbb{R}$ so dass (A − θI) regulär ist.

Für k = 1,2,....

1. $q_k=\frac{x_{k-1}}{\|x_{k-1}\|}$
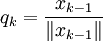
2. Löse (A − θI)x_k = q_k

Über den Rayleigh-Quotienten erhält man eine Näherung für den zugehörigen Eigenwert.

$\lambda_k=\frac{x_k^TAx_k}{x_k^Tx_k}$

Erweiterungen

Wählt man in jedem Schritt über θ = λ_k einen neuen Shift so erhält man die Rayleigh-Quotienten-Iteration.

Literatur

• Gene H. Golub / Charles F. van Loan Matrix Computations
• J.H. Wilkinson The Algebraic Eigenvalue Problem