Wigner-Eckart

Das Wigner-Eckart-Theorem (nach Eugene Paul Wigner und Carl Henry Eckart) ist ein Hilfsmittel für die Berechnung der Matrixelemente eines Tensoroperators, wenn dessen Symmetrieeigenschaften bekannt sind. Das Wigner-Eckart-Theorem darf nicht mit dem Wigner-Theorem verwechselt werden.

Für die definierenden Transformationseigenschaften eines Tensoroperators gilt:

$U^\dagger T_q^{(k)} U= \sum_{q'=-k}^k D_{qq'}^{(k)*} T_{q'}^{(k)}$

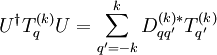
wobei U die unitäre Gruppentransformationsmatrix und 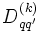$D_{qq'}^{(k)}$ eine irreduzible Darstellung dieser Gruppe in der Basis | α,jm > ist.

Def: Das Matrixelement eines Tensoroperators ausgedrückt in den Eigenzuständen des Drehimpulsoperators erfüllt folgende Gleichung:

$\langle\alpha', j'm'|T_q^{(k)}|\alpha, jm\rangle = \langle jk; j'm'|jk; mq\rangle\frac{\langle\alpha'j'||T^{(k)}||\alpha j\rangle}{\sqrt{2j+1}}$

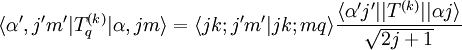
wobei das reduzierte Matrixelement (gekennzeichnet durch die 2 Striche beiderseits von T^(k)) unabhängig von m und m' sowie q ist. Darin besteht auch der Vorzug, denn dieses von m und m' unabhängige Matrixelement wird ein Mal berechnet und ist dann für alle anderen Matrixelemente gleich und ermöglicht somit eine einfache Berechnung beliebiger Matrixelemente.

Hierbei ist T^(k) ein Tensor des Rangs k, j der Gesamtdrehimpuls, m die zugehörige magnetische Quantenzahl und α alle weiteren zur Beschreibung des Systems nötigen Quantenzahlen des Zustandes.

Für Rotationssymmetrie sind die 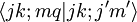$\langle jk; mq|jk; j'm'\rangle$ die Clebsch-Gordan-Koeffizienten.

Literatur

• Eckart, C.: The Application of Group Theory to the Quantum Dynamics of Monatomic Systems. Rev. Mod. Phys. 2, 305-380, 1930.
• Sakurai, J.J.: Modern Quantum Mechanics, Addison-Wesley, 239-240, 1994
• Wigner, E. P.: Einige Folgerungen aus der Schrödingerschen Theorie für die Termstrukturen. Z. Physik 43, 624-652, 1927.