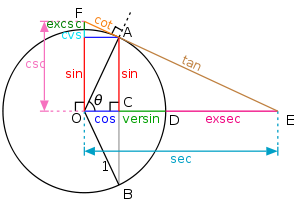
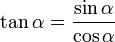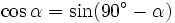- Winkelbeziehung
-
Mit trigonometrischen Funktionen oder auch Winkelfunktionen bezeichnet man rechnerische Zusammenhänge zwischen Winkel und Seitenverhältnissen (ursprünglich in rechtwinkligen Dreiecken). Tabellen mit Verhältniswerten für bestimmte Winkel ermöglichen Berechnungen bei Vermessungsaufgaben, die Winkel und Seitenlängen in Dreiecken nutzen.
Inhaltsverzeichnis
Übersicht der trigonometrischen Funktionen
Die elementaren trigonometrischen Funktionen sind:
-
- die Sinusfunktion (abgekürzt: sin),
- die Kosinusfunktion (abgekürzt: cos),
- die Tangensfunktion (abgekürzt: tan oder tg)
sowie deren Kehrwertfunktionen
-
- Kosekansfunktion (Kehrwert des Sinus: csc)
- Sekansfunktion (Kehrwert des Kosinus: sec)
- Kotangensfunktion (Kehrwert der Tangens: cot)
Zwischen diesen Funktionen bestehen enge Zusammenhänge. Genau genommen würde bereits eine der Funktionen ausreichen, um beliebige trigonometrische Probleme lösen zu können. Die Verwendung mehrerer verschiedener Funktionen ermöglicht jedoch eine Vereinfachung der Rechnungen und Formeln.
Die Kotangensfunktion wird in Tabellen mit Funktionswerten von trigonometrischen Funktionen gerne genutzt, da man cot(x) zusammen mit der Tangensfunktion tabellieren kann. Insofern ist die Bedeutung von cot(x) etwas größer als die von sec(x) und csc(x).
Es gibt weitere - heute eher unübliche - Funktionen, wie z.B. sinus versus (versin), cosinus versus (coversin), exsecant (exsec) und excosecant (excsc).
Definition
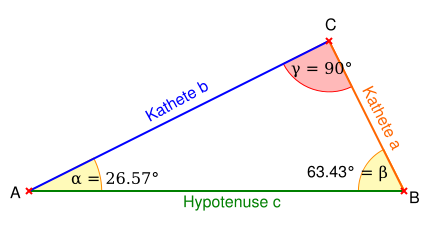
Ursprünglich sind die Winkelfunktionen als Seitenverhältnisse in rechtwinkligen Dreiecken und daher nur für Winkel von 0 bis 90 Grad definiert:
Diese Definition ist unabhängig von der Wahl des rechtwinkligen Dreiecks, das zur Berechnung verwendet wird. In jedem rechtwinkligen Dreieck mit Winkel α ergeben diese Verhältnisse den gleichen Wert. Dies lässt sich z.B. mit den Strahlensätzen beweisen.
Aus diesen Beziehungen folgt unmittelbar die Beziehung:
Die Ankathete des Winkels ist gleichzeitig die Gegenkathete des anderen spitzen Winkels β des rechtwinkligen Dreiecks; da die Winkelsumme im Dreieck 180° beträgt, und der rechte Winkel 90° zu dieser Summe beiträgt, ist dieser Winkel
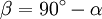 und daher
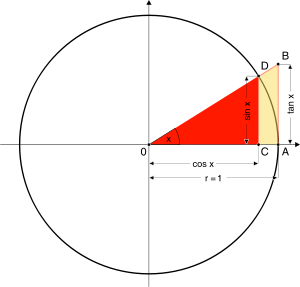
und daherDie Winkelfunktionen können aber als Sekanten- und Tangentenabschnitte am Einheitskreis auch auf größere Winkel erweitert werden. Vom Schnittpunkt des einen Winkelschenkels mit dem Einheitskreis werden die Lote auf die beiden Koordinatenachsen gefällt und liefern Sinus und Kosinus des Winkels. Die Tangenten in den Punkten x = 1 bzw. y = 1 schneiden den Schenkel ebenfalls und liefern dann in der Projektion auf die Achsen den Tangens und den Kotangens. Dabei muss der Schenkel gegebenenfalls rückwärts verlängert werden, um einen Schnittpunkt zu erzielen. Auf diese Weise können jedem Winkel von 0 bis 360 Grad Werte der Winkelfunktionen zugeordnet werden, die nun freilich auch negativ werden können (siehe Abbildung). Die oben angegebenen Beziehungen gelten dabei weiterhin.
In der Analysis werden Sinus und Kosinus in der Regel über Potenzreihen definiert, wobei der Winkel im Bogenmaß angegeben wird. Näheres siehe in den Artikeln Sinus und Kosinus sowie Tangens.
Umrechnungstabelle
Die Vorzeichen der trigonometrischen Funktionen in Abhängigkeit vom Quadranten gibt die folgende Tabelle an:
Quadrant sin und csc cos und sec tan und cot I + + + II + − − III − − + IV − + − Der Betrag wird wie folgt umgerechnet:
sin cos tan cot sec csc sin(x) 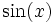
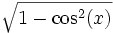
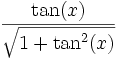
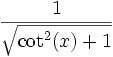
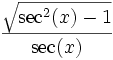
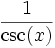
cos(x) 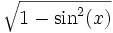
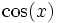
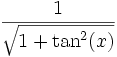
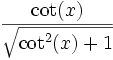
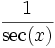
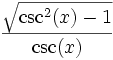
tan(x) 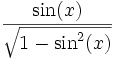
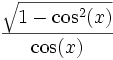
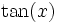
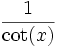
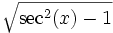
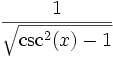
cot(x) 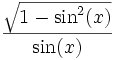
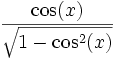
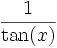
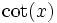
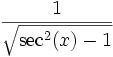
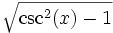
sec(x) 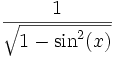
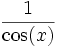
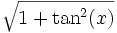
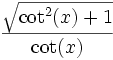
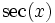
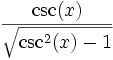
csc(x) 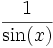
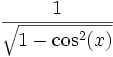
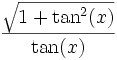
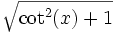
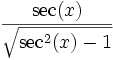
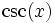
Anwendung der trigonometrischen Funktionen
Hauptsächlich werden die trigonometrischen Funktionen im Vermessungswesen genutzt. Für eine Liste von Formeln zur Berechnung von Größen am Dreieck siehe den Artikel Dreiecksgeometrie.
Weiterhin sind sie in der Analysis und bei vielen Anwendungen der Physik wichtig. Es besteht eine enge Beziehung zur Exponentialfunktion, die besonders bei Funktionen komplexer Zahlen und in der Taylorreihe der Funktionen sichtbar wird.
Umkehrung der trigonometrischen Funktionen
In manchen Situationen werden die trigonometrischen Winkelfunktionen benötigt, um aus Seitenverhältnissen Winkel zu berechnen. Dazu werden die Arkusfunktionen oder inverse Winkelfunktionen arcsin, arccos, arctan und arccot - die Umkehrfunktionen zu den trigonometrischen Funktionen - verwendet. Auf Taschenrechnern sind sie häufig mit sin-1 usw. bezeichnet. Das stimmt mit der Schreibweise f − 1 für die Umkehrfunktion von f überein (auch wenn die Arkusfunktionen das genau genommen nicht sind), kollidiert allerdings mit der ebenso üblichen Konvention, sink(x) für (sin(x))k zu schreiben.
Die Arkusfunktionen werden verwendet, um zu einem Seitenverhältnis den Winkel zu berechnen. Wegen der Symmetrie der trigonometrischen Funktionen ist von Fall zu Fall zu klären, in welchem Quadrant der gesuchte Winkel liegt.
Siehe auch
Weblinks
Trigonometrische FunktionPrimäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und KosekansUmkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und ArkuskosekansHyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans HyperbolicusAreafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus -
Wikimedia Foundation.