- Wohldefiniert
-
Man kann in der Mathematik ein Objekt nicht nur durch eine Definitionsgleichung (explizit), sondern auch durch eine charakteristische Eigenschaft (implizit) definieren. Während eine explizite Definition immer zulässig ist, ist eine implizite Definition nur unter der Bedingung zulässig, dass es tatsächlich genau ein Objekt mit der angegebenen Eigenschaft gibt. Diese Bedingung nennt man die Wohldefiniertheit der impliziten Definition.
Den Beweis der Wohldefiniertheit kann man in zwei Teile zerlegen: die Existenz und die Eindeutigkeit des zu definierenden Begriffs.
Implizite Definitionen tauchen oft unbemerkt auf, wenn man Abbildungen auf Faktormengen definiert. Das Ergebnis wird durch eine Abbildung auf einem Repräsentanten definiert. Wohldefiniertheit läuft hier auf die Unabhängigkeit des Ergebnisses von der Wahl des Repräsentanten hinaus.
Inhaltsverzeichnis
Einfaches Beispiel
- „Für alle
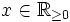 ist f1(x) definiert als diejenige Zahl
ist f1(x) definiert als diejenige Zahl 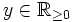 , für die gilt x = y2.“
, für die gilt x = y2.“ - „Für alle
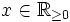 ist f2(x) definiert als diejenige Zahl
ist f2(x) definiert als diejenige Zahl 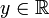 , für die gilt x = y2.“
, für die gilt x = y2.“ - „Für alle
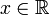 ist f3(x) definiert als diejenige Zahl
ist f3(x) definiert als diejenige Zahl 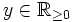 , für die gilt x = y2.“
, für die gilt x = y2.“
Zu 1: Die Wohldefiniertheit von f1(x) besagt, dass es für jede Zahl
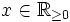 genau eine Zahl
genau eine Zahl 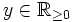 gibt mit der Eigenschaft x = y2. Das ist in der Tat der Fall, denn die Quadratfunktion von
gibt mit der Eigenschaft x = y2. Das ist in der Tat der Fall, denn die Quadratfunktion von  nach
nach  ist bijektiv. Die Funktion f1 ist also wohldefiniert – f1 ist die Quadratwurzelfunktion.
ist bijektiv. Die Funktion f1 ist also wohldefiniert – f1 ist die Quadratwurzelfunktion.Zu 2: Wohldefiniertheit gilt hier nicht, denn zum Beispiel gilt 4 = 22 und 4 = ( − 2)2. Die Eindeutigkeit ist verletzt.
Zu 3: Auch hier gilt Wohldefiniertheit nicht, denn − 1 = y2 hat keine reellen Lösungen y. Die Existenz ist verletzt.
Repräsentantenunabhängigkeit
In der Literatur findet sich häufig die Definition von Wohldefiniertheit als Repräsentantenunabhängigkeit.[1] Vereinzelt wird ausdrücklich darauf hingewiesen, dass es keine darüber hinaus gehende Bedeutung gibt.[2]
Die Repräsentantenunabhängigkeit soll zunächst an einem Beispiel erläutert werden. Jede rationale Zahl lässt sich als Bruch aus zwei ganzen Zahlen, dem Zähler und dem Nenner, schreiben. „Definieren“ wir also
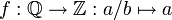 als Funktion, die jeder rationalen Zahl ihren Zähler zuordnet.
als Funktion, die jeder rationalen Zahl ihren Zähler zuordnet.Es gilt bekanntlich 1 / 2 = 2 / 4, also gilt 1 = f(1 / 2) = f(2 / 4) = 2, ein Widerspruch! Die Definition von f kann also nicht in Ordnung sein. Die Definition von f ist tatsächlich eine implizite Definition und sie ist nicht wohldefiniert. Sehen wir uns dazu die Definition von f genauer an: Der Bruch a / b steht für die Äquivalenzklasse aller Paare (x,y), für die gilt ay = xb. Die Definition von f müsste also genauer lauten: Für alle rationalen Zahlen q ist f(q) definiert als derjenige Wert x für den es ein y gibt mit
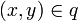 . Nun stellt sich heraus, dass es mehrere solcher x gibt, zum Beispiel 1 (mit y = 2) oder 2 (mit y = 4). Die Wohldefiniertheit gilt also nicht.
. Nun stellt sich heraus, dass es mehrere solcher x gibt, zum Beispiel 1 (mit y = 2) oder 2 (mit y = 4). Die Wohldefiniertheit gilt also nicht.Hat ein Element
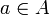 also mehrere Darstellungen (im Beispiel: 1 / 2, 2 / 4, 3 / 6, …), dann muss eine Funktion
also mehrere Darstellungen (im Beispiel: 1 / 2, 2 / 4, 3 / 6, …), dann muss eine Funktion 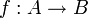 diesem Element einen Wert f(a) zuordnen, der von der Darstellung von a unabhängig ist. Die Definition
diesem Element einen Wert f(a) zuordnen, der von der Darstellung von a unabhängig ist. Die Definition 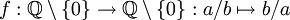 zum Beispiel erfüllt diese Bedingung.
zum Beispiel erfüllt diese Bedingung.Für zwei mathematische Konzepte muss die Repräsentantenunabhängigkeit nachgewiesen werden:
Induzierte Abbildungen
Definition der induzierten Abbildung
Gegeben seien zwei Mengen A und B sowie die Äquivalenzrelationen
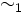 auf A und
auf A und 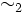 auf B. [a]1 bezeichne die Äquivalenzklasse des Elements
auf B. [a]1 bezeichne die Äquivalenzklasse des Elements 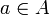 bezüglich
bezüglich 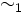 und [b]2 die Äquivalenzklasse des Elements
und [b]2 die Äquivalenzklasse des Elements 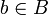 bezüglich
bezüglich 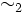 . Die Menge der Äquivalenzklassen
. Die Menge der Äquivalenzklassen ![A_{/\sim_1} := \{[a]_1 \mid a \in A\}](/pictures/dewiki/52/476780ce4f3d7990adcdc1862a214ee7.png) heißt auch Faktormenge.
heißt auch Faktormenge.Hat man nun eine Funktion
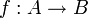 gegeben, so ergibt sich eine dazugehörige Funktion
gegeben, so ergibt sich eine dazugehörige Funktion 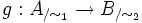 auf der Faktormenge gemäß der Vorschrift
auf der Faktormenge gemäß der Vorschrift![\ g([a]_1) := [f(a)]_2](/pictures/dewiki/49/13c8598a39500c994d4aa2b2815560d7.png) .
.
g heißt die von f induzierte Abbildung.
Wohldefiniertheit bei induzierten Abbildungen
Um die Wohldefiniertheit von g zu zeigen, ist nachzuweisen, dass der Wert g([a]1) unabhängig vom ausgewählten Repräsentanten a der Äquivalenzklasse [a]1 ist. Anders gesagt muss gelten:
- Falls [x]1 = [y]1, dann folgt [f(x)]2 = [f(y)]2.
Beispiele für induzierte Abbildungen
Im ersten Beispiel sei
 und B = {0,1}. Als Äquivalenzrelation
und B = {0,1}. Als Äquivalenzrelation 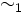 wählen wir die „Äquivalenz modulo 3“, d. h., es gelte
wählen wir die „Äquivalenz modulo 3“, d. h., es gelteDie Äquivalenzrelation
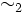 sei die gewöhnliche Gleichheit, also
sei die gewöhnliche Gleichheit, also 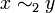 , falls x = y. Als Funktion wählen wir
, falls x = y. Als Funktion wählen wirDie induzierte Abbildung ist dann
Es gilt nun
![g([5]_1) = [1]_2 = \{1\} \neq \{0\} = [0]_2 = g([8]_1)](/pictures/dewiki/100/d207433b8d0483800bd202d4d6ee68d3.png) , obwohl [5]1 = [8]1. In diesem Fall ist also die induzierte Abbildung g nicht wohldefiniert.
, obwohl [5]1 = [8]1. In diesem Fall ist also die induzierte Abbildung g nicht wohldefiniert.
Im zweiten Beispiel sei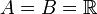 . Die Äquivalenzrelation
. Die Äquivalenzrelation 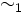 sei erklärt durch
sei erklärt durchund
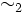 sei wieder die gewöhnliche Gleichheit. Der reelle Kosinus induziert nun die Abbildung
sei wieder die gewöhnliche Gleichheit. Der reelle Kosinus induziert nun die Abbildung![g: \mathbb{R}_{/\sim_1} \to \mathbb{R}, [x]_1 = \cos(x)](/pictures/dewiki/54/6b5b811bb4debbf4b9129e778aaff759.png) .
.
Diese Abbildung ist wohldefiniert, wie man folgendermaßen zeigt:
Seien
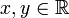 mit der Eigenschaft [x]1 = [y]1. Gemäß der Definition von
mit der Eigenschaft [x]1 = [y]1. Gemäß der Definition von 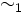 existiert nun ein
existiert nun ein  mit
mit 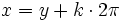 , und deshalb folgt
, und deshalb folgt ![g([x]_1) = \cos(x) = \cos(y + k \cdot 2\pi) = \cos(y) = g([y]_1)](/pictures/dewiki/48/0c3b4c836e89837a15320a9b9db37cb8.png) , wobei wir die Tatsache verwendet haben, dass der Kosinus eine Periode von 2π besitzt.
, wobei wir die Tatsache verwendet haben, dass der Kosinus eine Periode von 2π besitzt.Induzierte Verknüpfung
Definition der Induzierten Verknüpfung
Sei A eine nichtleere Menge mit der inneren Verknüpfung
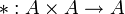 . Zu einer Äquivalenzrelation
. Zu einer Äquivalenzrelation 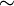 auf A und der zugehörigen Faktorstruktur
auf A und der zugehörigen Faktorstruktur 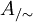 definiert man die von * auf der Faktorstruktur induzierte Verknüpfung als
definiert man die von * auf der Faktorstruktur induzierte Verknüpfung alsWohldefiniertheit für induzierte Verknüpfungen
Verschiedene Repräsentanten derselben Klassen müssen stets dasselbe Ergebnis liefern, um von einer wohldefinierten Verknüpfung auf der Faktorstruktur sprechen zu können. Es ist also zu zeigen, dass für alle
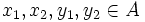 mit der Eigenschaft
mit der Eigenschaft 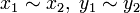 gilt
giltBeispiele für induzierte Verknüpfungen
- Die Verknüpfung
 , gegeben durch p([a],[b]): = [ | a | | b | ], ist nicht wohldefiniert: Es gilt [5] = [2] und [3] = [6], aber
, gegeben durch p([a],[b]): = [ | a | | b | ], ist nicht wohldefiniert: Es gilt [5] = [2] und [3] = [6], aber
![p([5],[3]) = [5^3] = [125] = [3\cdot 41+2] = [2] \neq [1] = [3\cdot 21+1] = [64] = [2^6] = p([2],[6])\](/pictures/dewiki/56/8fe7fc8b264e0b769f4493b0db5cb17b.png) .
.
- Betrachte die symmetrische Gruppe S3 = {id,(1,2),(1,3),(2,3),(1,2,3),(1,3,2)} und darin die Untergruppe U: = {id,(1,2)}. Die auf der Faktormenge S3 / U induzierte Verknüpfung ist nicht wohldefiniert. Es ist [id] = [(1,2)] und selbstverständlich [(1,3,2)] = [(1,3,2)], aber
- Die Addition und die Multiplikation in einem Restklassenring

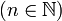 sind wohldefiniert. Die Restklassen-Addition ist gerade die von der Addition in
sind wohldefiniert. Die Restklassen-Addition ist gerade die von der Addition in  und dem Normalteiler
und dem Normalteiler 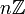 induzierte Verknüpfung.
induzierte Verknüpfung.
- Ist N ein Normalteiler der Gruppe G, dann ist die auf G / N induzierte Verknüpfung wohldefiniert, und G / N heißt Faktorgruppe. Die Eigenschaft, Normalteiler zu sein, ist sogar äquivalent dazu, dass die induzierte Verknüpfung auf der Faktormenge G / H wohldefiniert ist.
Vollständigkeit und Widerspruchsfreiheit
In einem weiteren Sinn wird Wohldefiniertheit auch auf andere Bereiche ausgedehnt. Sie bezeichnet dann eine sinnvolle und widerspruchsfreie Definition. Synonym für „nicht wohldefiniert“ in diesem Sinn werden auch „nicht definiert“ oder „nicht vollständig definiert“ gebraucht.
Definitionsbereich einer Funktion
Hat man zum Beispiel die Formel
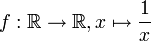 , so darf die Null nicht im Definitionsbereich enthalten sein, da für x = 0 die Formel
, so darf die Null nicht im Definitionsbereich enthalten sein, da für x = 0 die Formel 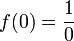 liefert. Durch Null zu teilen, ist in den reellen Zahlen allerdings nicht erklärt, d. h., es gibt keine reelle Zahl „1 / 0“. (In einem erweiterten Sinne könnte man zwar
liefert. Durch Null zu teilen, ist in den reellen Zahlen allerdings nicht erklärt, d. h., es gibt keine reelle Zahl „1 / 0“. (In einem erweiterten Sinne könnte man zwar 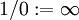 setzen. Das tut dem Beispiel aber nichts, da
setzen. Das tut dem Beispiel aber nichts, da  keine reelle Zahl ist! Zudem müsste man
keine reelle Zahl ist! Zudem müsste man  und
und  miteinander identifizieren, da f(x) für
miteinander identifizieren, da f(x) für  gegen
gegen  divergiert.)
divergiert.)Ebenso ist es in den reellen Zahlen nicht erklärt, die Quadratwurzel aus negativen Zahlen zu ziehen. Anders gesagt wäre die „Funktion“
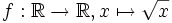 nicht wohldefiniert, die Funktion
nicht wohldefiniert, die Funktion 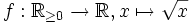 hingegen schon.
hingegen schon.Wertebereich einer Funktion
Schreibt man die Formel f(x) = 2x als „Funktion“
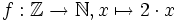 , so wird dem Wert x = − 2 zwar der Wert f( − 2) = − 4 zugeordnet. Das ist in diesem Fall aber nicht zulässig, da − 4 keine natürliche Zahl ist und somit nicht im Wertebereich liegt.
, so wird dem Wert x = − 2 zwar der Wert f( − 2) = − 4 zugeordnet. Das ist in diesem Fall aber nicht zulässig, da − 4 keine natürliche Zahl ist und somit nicht im Wertebereich liegt.Verknüpfungen bei Gruppen
Innere Verknüpfungen einer algebraischen Struktur G (z. B. einer Gruppe) sind ebenfalls Funktionen (meist mit zwei Argumenten). Für sie gelten also dieselben Bedingungen: Die Verknüpfung von Elementen der Struktur G muss ein eindeutig bestimmtes Element von G ergeben. Hier wird oft fälschlicherweise der Ausdruck Abgeschlossenheit benutzt, welcher sich aber auf die Definition von Unterstrukturen bezieht.
Wohldefiniertheit von Mengen
Eine Menge ist wohldefiniert, wenn das Definiens für jedes beliebige Objekt eindeutig festlegt, dass es entweder Element der Menge ist oder nicht Element der Menge ist. Insbesondere werden so gewisse Formen imprädikativer Definitionen ausgeschlossen.
Einzelnachweise
- ↑ Serge Lang: Algebra. 3. Auflage. 1993, S. X (Prerequisites).
- ↑ Albrecht Beutelspacher: Das ist o.B.d.A trivial! Braunschweig 1997, S. 9.
Weblinks
- Eric W. Weisstein: wohldefiniert auf MathWorld (englisch)
- wohldefiniert auf PlanetMath (engl.)
- Definition und wohldefiniert auf Mathe-Online
- „Für alle
Wikimedia Foundation.


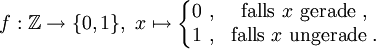
![g : \mathbb{Z}_{/\sim_1} \to \{0, 1\}_{/\sim_2}, \ [x]_1 \mapsto [f(x)]_2 = \left\{\begin{matrix}
\{0\}\ , & \mbox{falls}\ x\ \mbox{gerade}\ , \\
\{1\}\ , & \mbox{falls}\ x\ \mbox{ungerade}\ .
\end{matrix}\right.](/pictures/dewiki/101/e1ff32733afcb6b685d839562641803e.png)

![* : A_{/\sim} \times A_{/\sim} \to A_{/\sim}, [a]*[b] := [a * b]\ .](/pictures/dewiki/54/603d35697e948b94c8566d0c7b9377e4.png)
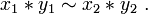
![[(1,2)*(1,3,2)] = [(1,3)] \neq [(1,3,2)] = [id*(1,3,2)].](/pictures/dewiki/56/8239a958f191105c1997f1d87affb130.png)