- Wronskideterminante
-
Mit Hilfe der Wronski-Determinante, die nach dem polnischen Mathematiker Josef Hoëné-Wroński benannt wurde, kann man skalare Funktionen auf lineare Unabhängigkeit testen, wenn diese hinreichend oft differenzierbar sind. Dies kann insbesondere beim Lösen einer gewöhnlichen Differentialgleichung ein nützliches Hilfsmittel sein. Für n reell- oder komplexwertige Funktionen
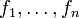 auf einem Intervall I ist die Wronski-Determinante definiert durch
auf einem Intervall I ist die Wronski-Determinante definiert durch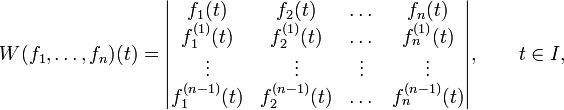
wobei in der ersten Zeile die Funktionen stehen und in den weiteren Zeilen die hochgestellten Zahlen in Klammern die erste bis (n − 1)-te Ableitung bezeichnen.
Die Berechnung der Wronski-Determinante von linearen, gewöhnlichen Differentialgleichungen zweiter Ordnung kann durch die Anwendung der abelschen Identität vereinfacht werden.
Inhaltsverzeichnis
Formulierung als Kriterium für lineare Unabhängigkeit
Gilt
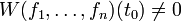 für ein
für ein 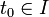 , so sind die Funktionen
, so sind die Funktionen 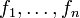 auf dem Intervall I linear unabhängig.
auf dem Intervall I linear unabhängig.Beweis
Aus
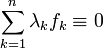 folgt
folgt 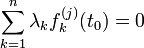 für alle
für alle 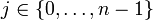 . Insbesondere erhält man eine Linearkombination der Spaltenvektoren der Wronski-Matrix im Punkt t0 zum Nullvektor. Da die Spaltenvektoren aber wegen
. Insbesondere erhält man eine Linearkombination der Spaltenvektoren der Wronski-Matrix im Punkt t0 zum Nullvektor. Da die Spaltenvektoren aber wegen 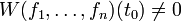 linear unabhängig sind, muss
linear unabhängig sind, muss 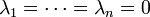 folgen.
folgen.
Gegenbeispiel für die Umkehrung
Vorsicht: Aus
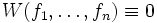 folgt nicht die lineare Abhängigkeit der Funktionen
folgt nicht die lineare Abhängigkeit der Funktionen 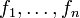 , d. h., die Umkehrung ist falsch.
, d. h., die Umkehrung ist falsch.Als Gegenbeispiel hierfür dienen beispielsweise die auf den reellen Zahlen definierten Funktionen
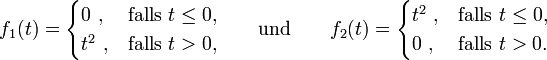
Für alle
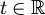 gilt
gilt 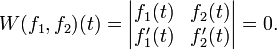
Aber
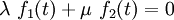 führt für
führt für 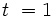 zu
zu 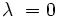 und für
und für 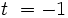 zu
zu 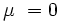 , was die lineare Unabhängigkeit der beiden Funktionen impliziert.
, was die lineare Unabhängigkeit der beiden Funktionen impliziert.Literatur
- Eric W. Weisstein. „Wronskian.“ From MathWorld -A Wolfram Web Resource. http://mathworld.wolfram.com/Wronskian.html
Wikimedia Foundation.
