Wurzel (Graphentheorie)

Unter einer Wurzel versteht man bei gerichteten Bäumen denjenigen Knoten von dem aus alle anderen Knoten im Baum erreichbar sind, und der selbst von keinem anderen Knoten aus erreichbar ist. Eine Wurzel ist somit der einzige Knoten in einem Baum welcher keinen Vorgänger hat. Zeichnet man einen Baum, so ist die Wurzel immer der oberste Knoten des Baumes. Bäume haben in der Informatik immer genau eine Wurzel. Zerlegt man den ursprünglichen Baum in mehrere Teilbäume, so haben auch die entsprechenden Teilbäume wieder genau eine bestimmte Wurzel. Verallgemeinert man den Begriff der Wurzel auf allgemeine Graphen, so spricht man auch von Quellen.

Definition

Ein Knoten ist eine Wurzel genau dann wenn gilt:

• Alle weiteren Knoten des Baumes sind von diesem Knoten aus erreichbar
• Der Knoten hat keinen Vorgänger

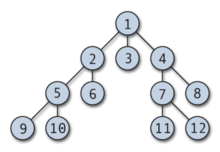
Beispiel

Beispielbaum

• Die Wurzel des Beispielbaumes hat die Marke 1.
• Die Wurzel des Teilbaumes welcher aus den Knoten 5,9 und 10 besteht hat die Marke 5
• Die Wurzel des Teilbaumes welcher nur aus dem Knoten 12 besteht hat die Marke 12