- Baum (Graphentheorie)
-
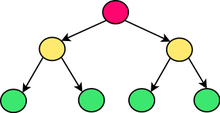
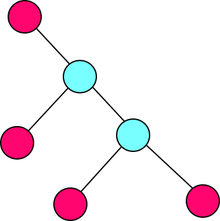
Ein Baum ist in der Graphentheorie ein spezieller Graph, mit dem sich eine Monohierarchie modellieren lässt. Je nachdem, ob die Kanten des Baums eine ausgezeichnete Richtung besitzen, lassen sich graphentheoretische Bäume unterteilen in ungerichtete Bäume und gewurzelte Bäume, und für gewurzelte Bäume in Out-Trees, bei denen die Kanten von der Wurzel ausgehen, und In-Trees, bei denen Kanten in Richtung Wurzel zeigen.
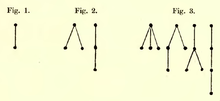 Darstellung aller Bäume[1] mit einer, zwei oder drei Kanten bei der ersten mathematischen Modellierung von Bäumen durch Arthur Cayley (1857)
Darstellung aller Bäume[1] mit einer, zwei oder drei Kanten bei der ersten mathematischen Modellierung von Bäumen durch Arthur Cayley (1857)
In der Informatik werden Bäume häufig als Datenstruktur eingesetzt. In diesem Fall werden sie aber anders repräsentiert als allgemeine Graphen. Durch Entfernen einer Kante zerfällt ein Baum in zwei Teilbäume und bildet damit einen so genannten Wald.
Inhaltsverzeichnis
Definition
Ein ungerichteter Baum ist ein zusammenhängender kreisfreier ungerichteter Graph. Die Knoten mit Grad 1 heißen Blätter, die übrigen Knoten heißen innere Knoten.
Ein gerichteter Baum ist ein gerichteter kreisfreier Graph mit genau einer Wurzel. Wurzeln sind Knoten mit Eingangsgrad 0. Knoten mit Ausgangsgrad 0 heißen Blätter.
Spezielle Bäume
Es existiert eine Vielzahl von Begriffen, die Bäume näher spezifizieren. So gibt es zum Beispiel
- leere Bäume (diese enthalten keine Knoten und Kanten),
- Binärbäume,
- Binomialbäume,
- balancierte Bäume und
- vollständige Binärbäume.
Äquivalente Charakterisierungen von Bäumen
Ein Graph G=(V,E) mit |V|=n Knoten und |E|=m Kanten kann durch folgende äquivalente Aussagen als Baum definiert werden:
- Zwischen je zwei Knoten von G gibt es genau einen Weg.
- G ist zusammenhängend und es gilt m=n-1. (Es gibt immer eine Kante weniger als Knoten.)
- G enthält keinen Zyklus und es gilt m=n-1.
- G ist (minimal) zusammenhängend und (maximal) azyklisch.
Bäume als Datenstruktur
Gewurzelte Bäume, insbesondere Out-Trees, werden häufig als Datenstruktur verwendet. Bei beschränkter Ordnung können diese so implementiert werden, dass jeder Knoten einen festen Satz an Variablen oder ein Array für die Referenzen auf seine Kinder enthält. Häufig besitzen die Knoten auch eine Referenz auf ihren Elternknoten (back pointer). Ein Baum unbeschränkter Ordnung kann implementiert werden, indem man statt Arrays dynamische Listen verwendet. In Programmiersprachen ohne dynamische Listen hat sich auch ein Verfahren bewährt, bei dem ein allgemeiner Baum durch einen Binärbaum implementiert wird:

Die rötliche Linie zeigt dabei den realisierten allgemeinen Baum, während die Pfeile die tatsächlichen Zeigerstrukturen repräsentieren. Das Grundprinzip besteht darin, dass ein Zeiger jeweils auf den am weitesten links stehenden Sohn zeigt, während der andere auf den rechten Bruder verweist. Hierbei ist zwar ein direkter Zugriff auf einzelne bestimmte Sohn-Knoten nicht mehr möglich, da man sich über die Geschwister voranarbeiten muss. Dafür ist diese Implementierung sehr speichereffizient.
Zeichnen von Bäumen
Die grafische Ausgabe eines Baums ist ein nicht triviales Problem. Allgemein gilt, dass jeder Baum planar, das heißt ohne Überschneidungen der Kanten gezeichnet werden kann. Je nach Anwendungszweck gibt es weitere Wünsche an die Art der Ausgabe:
- alle Kanten sind gerade Linien
- alle Knoten haben ganzzahlige Koordinaten
- möglichst kleiner Platzbedarf bei möglichst ästhetischem Ergebnis
- alle Kanten von Vater zum Kind streng monoton fallend
Es gibt verschiedene Algorithmen, deren Ergebnisse recht verschieden aussehen. Meist lösen sie nur einige, aber nicht alle Wünsche an die Ausgabe. Bekannte Algorithmen sind die HV-Bäume (Horizontal-Vertikal) und der Algorithmus von Walker.
Anzahl von Bäumen
Es gibt nn − 2 verschiedene bezeichnete Bäume mit n Knoten. Diese Aussage ist als Satz von Cayley bekannt.
Siehe auch
Quellen
Literatur
- Frank Gurski, Irene Rothe, Jörg Rothe, Egon Wanke: Exakte Algorithmen für schwere Graphenprobleme, Springer-Verlag, Berlin Heidelberg, 2010, ISBN 978-3-642-04499-1
Anmerkungen
Wikimedia Foundation.