Bellmann-Ford

Der Algorithmus von Bellman und Ford (nach seinen Erfindern Richard Bellman und Lester Ford) ist ein Algorithmus der Graphentheorie und dient der Berechnung der kürzesten Wege ausgehend von einem Startknoten in einem kantengewichteten Graphen. Gelegentlich wird auch vom Moore-Bellman-Ford-Algorithmus gesprochen, da auch Edward F. Moore zu seiner Entwicklung beigetragen hat.

Anders als beim Algorithmus von Dijkstra, dem bekanntesten Verfahren zur Suche nach kürzesten Wegen in Graphen, können die Gewichte der Kanten auch negativ sein. Kreise negativer Länge, die vom Startknoten aus erreichbar sind, müssen jedoch ausgeschlossen werden, da diese sonst beliebig oft durchlaufen werden könnten. Damit könnte bei jedem erneuten Durchlauf des Kreises ein Weg mit kürzerer Länge konstruiert werden. Das Problem wäre damit nicht wohlgestellt.

Der Algorithmus erkennt jedoch Kreise negativer Länge und bricht in diesem Fall selbstständig ab.

Algorithmus

G bezeichnet den gewichteten Graphen mit V als Knotenmenge und E als Kantenmenge. Gewicht ist die Gewichtsfunktion des Graphen und bestimmt die Distanz von zwei Knoten, die durch eine Kante verbunden werden. s ist der Startknoten, von dem ausgehend die kürzesten Wege zu allen anderen Knoten berechnet werden, und n ist die Anzahl der Knoten in V.

Wenn die Ausführung des Algorithmus endet, kann der Ausgabe entnommen werden, ob G einen Kreis negativer Länge besitzt. Falls dies nicht der Fall ist, enthält Distanz die Abstände aller Knoten zu s. Um von einem Knoten auf dem kürzesten Weg zum Startknoten s zu gelangen, muss man also so lange den Knoten besuchen, der durch Vorgänger(v) gegeben ist, bis man s erreicht hat. Genauer gesagt wird durch Vorgänger ein Spannbaum definiert, der die von s aus ausgehenden minimalen Wege in Form eines In-Trees speichert.

01  für jedes v aus V                   
02      Distanz(v) := unendlich, Vorgänger(v) := kein
03  Distanz(s) := 0

04  wiederhole n - 1 mal               
05      für jedes (u,v) aus E
06          wenn Distanz(u) + Gewicht(u,v) < Distanz(v)
07          dann
08              Distanz(v) := Distanz(u) + Gewicht(u,v)
09              Vorgänger(v) := u

10  für jedes (u,v) aus E                
11      wenn Distanz(u) + Gewicht(u,v) < Distanz(v) dann
12          STOP mit Ausgabe "Kreis negativer Länge gefunden"

13  Ausgabe Distanz

Grundlegende Konzepte und Verwandtschaften

Im k-ten Schleifendurchlauf (04 - 09) wird der Abstand des kürzesten Weges mit maximal k Kanten berechnet. Ein Weg ohne Kreise enthält maximal n Knoten, also n - 1 Kanten. Falls in (10 - 12) festgestellt wird, dass ein Weg nicht optimal ist, muss dieser folglich einen Kreis mit negativem Gewicht enthalten.

Schneller als der Bellman-Ford-Algorithmus ist der Algorithmus von Dijkstra, ein Greedy-Algorithmus zur Suche kürzester Wege, der sukzessive den nächstbesten Knoten, der einen kürzesten Weg besitzt, aus einer Priority Queue in eine Ergebnismenge S aufnimmt. Sein Nachteil besteht jedoch darin, dass er als Eingabe nur Graphen mit nichtnegativen Gewichten zulässt. Der A*-Algorithmus erweitert den Algorithmus von Dijkstra um eine Abschätzfunktion. Ein anderes Verfahren zur Suche kürzester Wege, das sich auf das Optimalitätsprinzip von Bellman stützt, ist der Floyd-Warshall-Algorithmus.

Komplexität

Die Laufzeit des Algorithmus ist in , wobei n die Anzahl der Knoten und m die Anzahl der Kanten im Graphen sind. Falls ein Knoten vom Startknoten aus nicht erreichbar ist, wird der Abstand formal als unendlich gesetzt. Wendet man den Algorithmus an, um kürzeste Wege von jedem Knoten zu jedem anderen Knoten zu finden, so beträgt die Komplexität $\mathcal{O} \left( |n|^2 \cdot |m| \right)$.

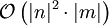Anwendungen

Der Bellman-Ford-Algorithmus findet unter anderem im Distanzvektoralgorithmus, einem dynamischen Routing-Algorithmus, Verwendung. Dieser wird z. B. vom Routing Information Protocol eingesetzt, mit dem Routingtabellen innerhalb einer administrativen Netzwerkdomain dynamisch erstellt werden (Interior Gateway Protocol).

Literatur

• L. R. Ford: Network flow theory, Paper P-923. The Rand Corporation, Santa Monica 1956
• R. E. Bellman: On a Routing Problem. In: Quarterly of Applied Mathematics. 16(1)/1958. Brown University, S. 87-90, ISSN 0033-569X
• E. F. Moore: The shortest path through a maze. In: Proceedings of the International Symposium on the Theory of Switching. 2/1959. Harvard University Press, S. 285-292
• L. R. Ford, D. R. Fulkerson: Flows in Networks., Princeton University Press, Princeton 1962, ISBN 0-691-07962-5

Andere Verfahren zur Berechnung kürzester Wege

• Algorithmus von Dijkstra
• A*-Algorithmus
• Floyd-Warshall-Algorithmus

Weblinks

• Ein interaktives Java-Applet zur Demonstration