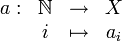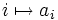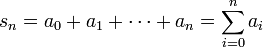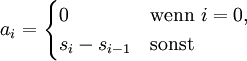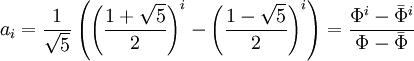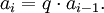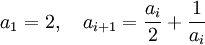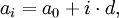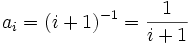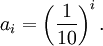Zahlenfolge

Als Folge wird in der Mathematik eine Auflistung (Familie) von endlich oder unendlich vielen fortlaufend nummerierten Objekten (beispielsweise Zahlen) bezeichnet. Dasselbe Objekt kann in einer Folge auch mehrfach auftreten. Das Objekt mit der Nummer i, man sagt hier auch: mit dem Index i, wird i-tes Glied oder i-te Komponente der Folge genannt. Unendliche Folgen kann man natürlich nicht vollständig auflisten. Hier muss ein Bildungsgesetz für die Folgenglieder bekannt sein oder sich aus den aufgeschriebenen Anfangsgliedern zweifelsfrei ergeben. Endliche wie unendliche Folgen finden sich in allen Bereichen der Mathematik. Mit unendlichen Folgen, deren Glieder Zahlen sind, beschäftigt sich vor allem die Analysis.

Ist n die Anzahl der Glieder einer endlichen Folge, auch Tupel genannt, so spricht man von einer Folge der Länge n, einer n-gliedrigen Folge oder von einem n-Tupel. Die Folge ohne Glieder, deren Index-Bereich also leer ist, wird leere Folge, 0-gliedrige Folge oder 0-Tupel genannt.

Beispiele

(1, 0, 0, 1, 1) 5-Tupel von ganzen Zahlen

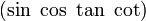$(\sin\ \cos\ \tan\ \cot)$ 4-Tupel trigonometrischer Funktionen

(2, 3, 5, 7, 11, 13 ...) Folge der Primzahlen

({} {1} {1,2} {1,2,3} ...) Unendliche Folge von Mengen

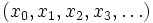$(x_0, x_1, x_2, x_3, \ldots)$ Allgemeine unendliche Folge, deren Terme fortlaufend indiziert sind. Als Indizierungsbeginn ist hier die Null gewählt.

Schreibweise

Allgemein schreibt man für eine Folge (a_i), also 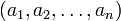$(a_1,a_2,\ldots,a_n)$ bei endlichen Folgen und 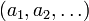$(a_1,a_2,\ldots)$ bei unendlichen Folgen. a_i steht dabei für ein beliebiges Folgenglied; die runde Klammer fasst diese zu einer Folge zusammen. Statt den runden Klammern werden manchmal auch spitze verwendet (also 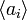$\langle a_i \rangle$); statt der Kommas können Semikolons verwendet werden, wenn eine Verwechslungsgefahr mit dem Dezimal-Komma besteht.

Der Unterschied zu der Menge der Folgenglieder {a_i} besteht darin, dass es auf die Reihenfolge der a_n ankommt, und dass ein bestimmtes a_i in der Folge auch mehrfach auftreten kann.

Beispiel: Die Folge (0, 1, 0, 2, 0, 4, …) hat die Bildmenge (oder unterliegende Menge) {0, 1, 2, 4, …}.

Formale Definition

Formal definiert ist eine unendliche Folge als eine Abbildung

$\begin{matrix} a:&\N &\to &X\\ & i &\mapsto &a_i \end{matrix}$

die jedem Index i aus der Indexmenge 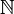$\N$ ein Folgenglied a_i aus der Zielmenge X zuordnet. Die Wahl des Anfangsindex ist jedoch letztlich willkürlich. In der Schulmathematik und in den häufigsten Anwendungsfällen ist X die Menge der reellen Zahlen $\R$. Es werden aber auch zum Beispiel Folgen von Mengen und Funktionenfolgen betrachtet.

Für eine endliche Folge (Sequenz) mit n Gliedern definiert man den Index statt aus 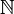$\N$ aus einer endlichen Menge, und zwar üblicherweise entweder aus der Menge 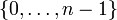$\{0, \ldots, n-1\}$ oder aus der Menge 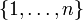$\{1, \ldots, n\}$. Gelegentlich findet sich für derartige Indexmengen die Notation <n_min,n_max>.

Anwendungen

Zeitreihen, wie sie zum Beispiel durch die Aufzeichnung von Temperaturbeobachtungen oder Wirtschaftsdaten entstehen, können mathematisch als Folgen aufgefasst werden.

In der Informatik kann man Felder (Arrays) als endliche Folgen auffassen.

Unendliche Folgen können gegen einen Grenzwert konvergieren. Die Theorie der Grenzwerte unendlicher Folgen ist eine wichtige Grundlage der Analysis, denn auf ihr beruhen die Berechnung von Grenzwerten von Funktionen, die Definition der Ableitung (Differentialquotient als Grenzwert einer Folge von Differenzenquotienten) und der riemannsche Integralbegriff. Wichtige Folgen erhält man als Koeffizienten von Taylorreihen stetiger Funktionen. Manche elementare Funktionen wie tan(x) führen dabei auf recht exotische Folgen, wie zum Beispiel die bernoullischen oder eulerschen Zahlen. Zum Beweis der Konvergenz ist die Methode der Vollständigen Induktion ein nützliches Hilfsmittel.

Eine Reihe ist eine spezielle Folge, deren einzelne Glieder sich aus der Summe der Glieder einer anderen Folge ergeben. Reihen finden in vielen Bereichen der Mathematik Anwendung. Siehe dazu den Artikel Reihe (Mathematik).

Bildungsgesetz einer Folge

Es gibt mehrere Möglichkeiten eine Folge anzugeben:

• Nennen aller Folgeglieder (nur endliche Folgen)
• Funktion
• Reihe
• Rekursion
• Algorithmus

Eine endliche Folge kann man angeben, indem man sämtliche Folgenglieder nennt. Bei einer unendlichen Folge geht das nicht, stattdessen muss man das Bildungsgesetz der Folge in anderer Form mitteilen.

Folgen, deren Bildungsgesetz sich als Funktionsvorschrift oder Rekursion mitteilen lässt, werden zuweilen regelmäßige Folgen genannt. Dies ist keine mathematisch strenge Klassifikation, da letzten Endes jede Folge, die überhaupt wohldefiniert ist, eine Funktionsvorschrift besitzt. Bei unregelmäßigen Folgen lässt sich lediglich sagen, dass die Angabe einer Funktionsvorschrift nach derzeitigem mathematischen Wissen aufwändig ist oder/und über algorithmische Vorschriften erfolgt, die mit der üblichen Notation nicht in funktionaler Form dargestellt werden können. Diese Thematik hängt mit der schwierigen Frage der Berechenbarkeit zusammen.

Angabe von Anfangsgliedern

Die in manchen Intelligenztests gestellte Aufgabe, eine Folge fortzusetzen, deren erste Glieder gegeben sind, ist aus mathematischer Sicht problematisch. Auch durch noch so viele Anfangsglieder ist der weitere Verlauf einer Folge nicht eindeutig festgelegt. Es gibt nur mehr oder weniger plausible Fortsetzungen.

Beispiele:

• Gegeben ist 0, 1, 2, 3. Am plausibelsten ist die Fortsetzung 4, 5, 6, ..., also die Folge aller natürlichen Zahlen. Möglich ist aber auch die Fortsetzung 0, 1, 2, 3, 0, ...., und zwar als die periodische Folge der kleinsten positiven Reste der natürlichen Zahlen modulo 4. In einem Computer werden ganze Zahlen oft mit 32 Bit im Zweierkomplement, also als die absolut kleinsten Reste modulo 2³² dargestellt. Beim sukzessiven Erhöhen eines Registers durchläuft man dann die Zahlenfolge 0, 1, 2, 3, ..., 2147483647, −2147483648, −2147483647, ..., −1 und periodisch weiter.
• Für die Zahlenfolge 3, 1, 4, 1, 5 ist eine plausible Fortsetzung 1, 6, 1, 7, ... Andere würden die Dezimaldarstellung der Kreiszahl π wiedererkennen und die Fortsetzung 9, 2, 6, ... vorschlagen.

Die Online-Enzyklopädie der Zahlenfolgen (OEIS) enthält tausende mathematisch relevanter Folgen. Darin kann man nach einer gegebenen Teilfolge suchen.

Angabe einer Funktionsvorschrift

Für viele, aber keineswegs alle Folgen kann man die Funktionsvorschrift

$i\mapsto a_i$

als eine geschlossene Gleichung angeben.

In den folgenden Beispielen legen wir Indizes aus der Menge 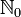$\mathbb{N}_0$ zugrunde:

• Die Folge der natürlichen Zahlen 0, 1, 2, 3, ... Dieses Beispiel ist speziell, weil die Werte von Folgenglied und Index übereinstimmen. Die Funktionsvorschrift lautet einfach

a_i = i.

• Die Folge der ungeraden Zahlen 1, 3, 5, 7, .... hat die Funktionsvorschrift

a_i = 2i + 1.

• Die Folge der Zweierpotenzen 1, 2, 4, 8, ...

a_i = 2ⁱ.

Daran anknüpfende Aufgaben

Das Problem, zu einer gegebenen Funktionsvorschrift die Anfangsglieder zu bestimmen, ist einfach lösbar. Man nimmt nacheinander die Werte i = 0, i = 1, i = 2 usw., setzt sie jeweils in die Funktionsvorschrift ein und berechnet auf diese Weise die Folgenglieder a₀, a₁, a₂ usw. Zweck dieser Rechnung ist es, sich ein erstes Bild vom Verlauf einer Folge zu machen. Aber Achtung: Eine Folge kann für wirklich große Indizes einen ganz anderen Verlauf nehmen als nach den ersten zehn oder hundert Gliedern zu erwarten war. Beispiel: die Folge a_i = 1 / (1 + (i − 1000)²), die bis i = 1000 monoton zunimmt, dann aber wieder abnimmt, wie man durch Einsetzen höherer Zehnerpotenzen überprüfen kann.

Die Umkehraufgabe, zu gegebenen Anfangsgliedern eine Funktionsvorschrift zu bestimmen, ist dagegen deutlich schwieriger. Streng genommen kann es gar keine eindeutige Lösung geben, denn jeder Folgenanfang lässt sich wie oben beschrieben in verschiedener Weise fortsetzen. In der Praxis wird diese Aufgabe daher nur für Folgen gestellt, deren Glieder a₀, a₁, a₂ usw. in einigermaßen überschaubarer Weise vom Index 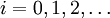$i=0, 1, 2, \dots$ abhängen. Im einzelnen können folgende Eigenschaften überprüft werden:

• Ist die Folge alternierend? Wenn ja, bekommt man das richtige Vorzeichen durch einen Faktor ( − 1)ⁱ in der Funktionsvorschrift. Beispiel: 0, −1, 2, −3, 4, … hat die Vorschrift $a_i=(-1)^i \cdot i$.
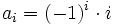• Sind die Folgeglieder Brüche? Wenn ja, konstruiere man unabhängig voneinander Funktionsvorschriften für Zähler und Nenner. Beispiel: 1/1, 2/2, 3/4, 4/8, … hat die Vorschrift a_i = (i + 1) / 2ⁱ.
• Nehmen die Folgenglieder um konstante Differenzen d zu (oder ab, mit d < 0) ? Wenn ja, hat man eine arithmetische Folge 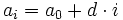$a_i=a_0 +d\cdot i$. Beispiel: 1, 3, 5, 7, … hat die Vorschrift a_i = 1 + 2i .
• Genügen die Differenzen zwischen aufeinander folgenden Glieder einem einfacheren Bildungsgesetz als die Folgeglieder selbst? Wenn ja, kann man die Folge als eine Reihe auffassen (siehe dazu unten). Beispiel: Für 1, 3, 6, 10, 15, … lauten die Differenzen 1, 2, 3, 4, ...
• Stehen aufeinander folgende Folgenglieder in einem konstanten Verhältnis 1:q zueinander? Wenn ja, hat man eine geometrische Folge 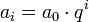$a_i=a_0 \cdot q^i$ . Beispiel: Die Folge 100; 80; 64; 51,2; … nimmt von Glied zu Glied um einen Faktor 0,8 ab; also lautet die Vorschrift $a_i = 100 \cdot (0{,}8)^i$ .

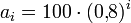Erschwert wird die Suche nach einer Funktionsvorschrift dadurch, dass die ersten ein oder zwei Folgenglieder (zu den Indizes 0 und 1) oft aus dem Rahmen zu fallen scheinen. Das liegt daran, dass ein Summand 0, ein Faktor 1 oder Exponent 0 oder 1 in aller Regel nicht ausgeschrieben, sondern sofort ausgerechnet werden. In der gekürzten Form 1, 1, 3/4, 1/2, … ist dem oben genannten Beispiel 1/1, 2/2, 3/4, 4/8, … die Funktionsvorschrift schwer anzusehen.

Angabe als Reihe

Eine Folge 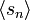$\langle s_n \rangle$, deren n-tes Glied als Summe der ersten n Glieder einer anderen Folge 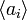$\langle a_i \rangle$ geschrieben werden kann, heißt eine Reihe:

$s_n= a_0 + a_1 +\cdots+a_n=\sum_{i=0}^n a_i$

Der mit Hilfe des Summenzeichens geschriebene Ausdruck 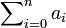$\sum\nolimits_{i=0}^n a_i$ ist eine Abkürzung für den Ausdruck 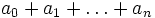$a_0+a_1+\ldots+a_n$. Innerhalb und außerhalb des Summenzeichens sind unterschiedliche Indizes zu verwenden. Dass wir speziell n und i gewählt haben, entspricht einer weit verbreiteten Konvention, ist aber nicht zwingend. Um 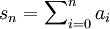$s_n=\sum\nolimits_{i=0}^n a_i$ als konkreten Zahlenwert zu berechnen, muss ein konkreter Zahlenwert für den Index n vorgegeben werden. Im Gegensatz dazu ist der Index i kein (von außen) vorzugebender Wert, sondern durch die Summationsvorschrift selbst festgelegt. Welches n auch immer gegeben ist, für den „Laufindex“ i müssen nacheinander die Werte 0, 1, ..., n eingesetzt und die Summe der zugehörigen a₀, a₁, ..., a_n berechnet werden.

Man kann jede Folge 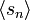$\langle s_n \rangle$ als eine Reihe auffassen, indem man aus den Differenzen aufeinander folgender Glieder eine zugehörige Folge

$a_i = \begin{cases}0 &amp;amp;\text{wenn }i=0,\\ s_i-s_{i-1} &amp;amp;\text{sonst}\end{cases}$

konstruiert. Folge und Reihe sind also nicht scharf voneinander trennbar. Die Zeitreihen der Wirtschaftswissenschaftler sind eigentlich Folgen. Viele Erklärungsmodelle modellieren aber nicht absolute Werte, sondern deren zeitliche Veränderungen, was für die Auffassung der absoluten Werte als Glieder einer Reihe spricht.

Konkreten Nutzen bringt die Deutung einer Folge als Reihe, wenn man die Summation für beliebige n ausführen kann. Summationsformeln sind zum Beispiel bekannt für die arithmetische Reihe und die geometrische Reihe.

Die Deutung einer unendlichen Folge als Reihe erleichtert es zu bestimmen, ob und wenn ja gegen welchen Grenzwert die Folge konvergiert. Für unendliche Reihen gibt es eigene Konvergenzkriterien. Umgekehrt kann man aus der Konvergenz einer Reihe (d. h., in obiger Schreibweise, der Konvergenz von (s_n)) immer darauf schließen, dass die Folge der „Summanden“ (in obiger Schreibweise also die Folge (a_n)) gegen Null konvergiert.

Angabe einer Rekursion

Das Bildungsgesetz einer Folge kann auch rekursiv angegeben werden. Dazu nennt man m Anfangswerte (mit 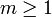$m \geq 1$; meistens ist m = 1 oder m = 2) sowie eine Vorschrift, wie ein Folgenglied a_i aus den vorhergehenden m Gliedern 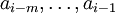$a_{i-m}, \ldots, a_{i-1}$ berechnet werden kann.

Das bekannteste Beispiel für eine Folge, die sich wesentlich einfacher durch eine Rekursionsvorschrift als durch eine Funktionsvorschrift beschreiben lässt, ist die Fibonacci-Folge 0, 1, 1, 2, 3, 5, 8, ... Für sie ist m = 2, gegeben sind die zwei Anfangsglieder a₀ = 0 und a₁ = 1 sowie die Rekursionsvorschrift

a_i = a_{i − 2} + a_{i − 1}.

Die explizite Formel von Moivre und Binet für die Folgeglieder

$a_i = \frac 1{\sqrt 5} \left(\left(\frac{1+\sqrt 5}2\right)^i - \left(\frac{1-\sqrt 5}2\right)^i\right) = \frac{\Phi^i - \bar\Phi^i}{\Phi - \bar\Phi}$

steht in engem Zusammenhang mit dem goldenen Schnitt und der goldenen Zahl Φ. Man beachte, dass die a_i alle ganzzahlig sind, da sich die ungeraden Potenzen der 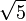$\sqrt 5$ herauskürzen.

Für manche Folgen kann man umgekehrt aus der Funktionsvorschrift eine Rekursionsvorschrift ableiten. Zum Beispiel folgt für die geometrische Folge aus der Funktionsvorschrift

$a_i = a_0\cdot q^i$

die Rekursionsvorschrift

$a_i = q\cdot a_{i-1}.$

Die Rekursion

$a_1 = 2,\quad a_{i+1} = \frac{a_i}2 + \frac1{a_i}$

definiert die Folge rationaler Zahlen 2, 3/2, 17/12, ..., die gegen 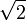$\sqrt 2$ konvergiert.

Angabe über einen Algorithmus

Für manche Folgen gibt es eine klar definierte Konstruktionsvorschrift, aber keine Funktionsvorschrift. Das bekannteste Beispiel ist die Folge der Primzahlen 2, 3, 5, 7, 11, ... Bereits den alten Griechen (möglicherweise auch Indern) war es bekannt, wie man immer weitere Glieder dieser Folge berechnet. Eine Möglichkeit ist, das Sieb des Eratosthenes anzuwenden. Es gibt jedoch keine Methode, zu einem gegebenen i die i-te Primzahl anzugeben, ohne zuvor die gesamte Folge von der ersten bis zur (i − 1)-sten Primzahl zu berechnen (oder nachzuschlagen). Wenn man nicht die zehnte oder die hundertste, sondern die 10²⁰-ste Primzahl wissen möchte, macht dies den Unterschied zwischen berechenbar und nicht berechenbar aus und hat weitreichende Implikationen für die Sicherheit von Verschlüsselungs- und Authentifizierungsalgorithmen, die auf Primzahlen beruhen.

Charakterisierung von Folgen

Wie Funktionen kann man auch Folgen über ihr Steigungsverhalten und ihren Bildbereich charakterisieren:

Monotonie

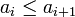Eine Folge heißt monoton steigend, wenn sie von Glied zu Glied gleichbleibt oder zunimmt, wenn also für alle i aus $\mathbb{N}$ gilt: $a_i \leq a_{i+1}$. Die Folge heißt streng monoton steigend, wenn sie von Glied zu Glied zunimmt, wenn also für alle i aus $\mathbb{N}$ gilt: a_i < a_{i + 1}. Die Begriffe monoton fallend und streng monoton fallend sind analog definiert.

Nachweis der Monotonie

Vermutet man, dass eine Folge nicht monoton (bzw. streng monoton) ist, setzt man ein paar Indizes in die Funktionsvorschrift ein, berechnet die zugehörigen Folgenglieder und hofft, ein Gegenbeispiel zu finden. Beispiel: Die durch a_i = 2ⁱ / (3i + 1) gegebene Folge ist nicht monoton, denn a₀ = 1 > a₂ = 4 / 7 aber a₂ < a₅ = 32 / 16.

Wenn man beispielsweise vermutet, dass eine Folge streng monoton fällt, schreibt man a_i > a_{i + 1}, wertet auf beiden Seiten die Funktionsvorschrift aus (indem man auf der rechten Seite i + 1 anstelle von i in die Vorschrift einsetzt), und überprüft die so entstandene Ungleichung, indem man sie durch Äquivalenzumformungen vereinfacht. Beispiel: 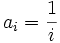$a_i=\frac{1}{i}$ führt auf 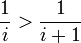$\frac 1i &amp;gt; \frac{1}{i+1}$, das ist äquivalent zu i + 1 > i bzw. zur wahren Aussage 1 > 0.

Manche Funktionsvorschriften lassen sich durch Termumformungen in eine Summe aus konstanten Termen und einer bekannten, einfacheren Folge zerlegen, deren Steigungsverhalten schon bekannt ist. Beispiel: 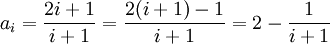$a_i = \frac{2i+1}{i+1} = \frac {2(i+1)-1}{i+1} = 2 - \frac {1}{i+1}$ . Wenn man weiß, dass 1 / (i + 1) streng monoton fällt, kann man schließen, dass − 1 / (i + 1) streng monoton steigt. Weil der Term 2 konstant ist, steigt auch a_i streng monoton.

Beschränktheit

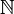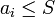Eine Folge heißt nach oben beschränkt, wenn sie eine obere Schranke S besitzt, so dass für alle i aus $\N$ gilt: $a_i \leq S$. Die kleinste obere Schranke einer Folge heißt auch ihr Supremum. Die Begriffe nach unten beschränkt, größte untere Schranke und Infimum sind analog definiert.

Nachweis der Beschränktheit/Bestimmung einer Schranke

Ein Nachweis per Gegenbeispiel ist hier nicht möglich, denn mit auch noch so vielen Beispielen kann man nicht sicherstellen, dass es nicht irgendeine sehr große bzw. sehr kleine Zahl gibt, durch die die Folge beschränkt ist.

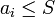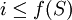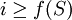Es muss also angenommen werden, dass es eine Schranke gibt. Nun wird die passende Ungleichung angesetzt, d. h. für eine obere Schranke also $a_i \leq S$. Auf der linken Seite der Ungleichung wird die Funktionsvorschrift angewandt und dann nach i aufgelöst. Dadurch erhält man (mit etwas Glück) ein Ergebnis der Form $i \leq f(S)$ oder $i \geq f(S)$, wobei f(S) für einen von S abhängigen Term steht. Im ersten Fall hat man herausgefunden, dass die Folge nicht nach oben beschränkt ist (egal wie groß f(S) ist, es ist immer möglich, ein noch größeres i zu finden, das die Ungleichung verletzt). Im zweiten Fall versucht man ein S zu finden, für das 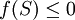$f(S) \leq 0$ ist. Für dieses S ist 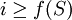$i \geq f(S)$ immer erfüllt und somit ist der Nachweis gelungen, dass S eine obere Schranke ist.

Auch hier lässt sich der Nachweis einfacher gestalten wenn es gelingt, die Funktionsvorschrift in eine Summe aus einfacheren Termen zu zerlegen.

Sonstige

• Eine Folge, deren Werte abwechselnd positiv und negativ sind, heißt alternierend.
• Eine Folge, deren Glieder alle übereinstimmen, wird konstante Folge genannt.
• Eine Folge, die gegen 0 konvergiert, heißt Nullfolge.
• Eine Folge, die aus Wiederholungen einer endlichen Teilfolge besteht, heißt periodisch. Es gibt eine Periodenlänge n, und für alle i aus 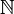$\N$ gilt: a_i = a_{i + n}. Teilfolge ist hier als Folge von [0,n] in die gewählte Menge zu verstehen.

Eine interessante Aufgabe aus der Analysis besteht darin, zu ermitteln, ob eine Folge konvergiert, und im Falle einer Konvergenz, wohin. Siehe dazu den Artikel Grenzwert. Eine unendliche Folge, die gegen keinen Grenzwert konvergiert, kann nichtsdestoweniger Häufungspunkte besitzen (Beispiel: die Folge −1/2, 3/4, −5/6, 7/8, ... besitzt die Häufungspunkte −1 und 1). Insbesondere hat jede beschränkte Folge mindestens einen Häufungspunkt (Satz von Bolzano-Weierstraß).

Die vorgenannte Charakterisierung einer Folge über ihr Steigungsverhalten und ihren Bildbereich kann helfen, zu bestimmen, ob und falls gegen welchen Grenzwert sie konvergiert. Besonders nützlich ist folgender Satz:

Eine monoton steigende, nach oben beschränkte Folge konvergiert und ihr Grenzwert stimmt mit ihrem Supremum überein (Beispiel: die Folge 0, 1/2, 2/3, 3/4, ... konvergiert gegen ihr Supremum 1). Eine monoton fallende, nach unten beschränkte Folge konvergiert gegen ihr Infimum.

Wichtige Folgen

Die allermeisten bekannten Folgen können in der On-Line Encyclopedia of Integer Sequences (OEIS) von Neil Sloane nachgeschlagen werden. Diese Datenbank enthielt im Februar 2009 über 155.000 Beschreibungen von Zahlenfolgen.

Arithmetische Folgen und Reihen

Hauptartikel: Arithmetische Folge

Eine arithmetische Folge ist eine Folge mit konstanter Differenz zwischen aufeinanderfolgenden Gliedern. Beispiele sind die häufig verwendeten Folgen der geraden Zahlen 2, 4, 6, ... mit der Funktionsvorschrift

a_i = 2i

und die der ungeraden Zahlen mit der Funktionsvorschrift

a_i = 1 + 2i.

Allgemein lautet die Funktionsvorschrift

$a_i = a_0 + i \cdot d,$

wobei d die konstante Differenz bezeichnet.

Folgen die sich auf arithmetische Folgen zurückführen lassen, nennt man Folgen höherer Ordnung. So ist die Folge der Dreieckszahlen eine arithmetische Folge 2. Ordnung.

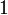
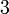
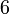
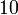
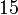
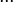
Folge:	$1\$		$3\$		$6\$		$10\$		$15\$		$...\$
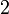
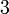
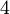
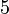
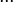
1. Differenzfolge:		$2\$		$3\$		$4\$		$5\$		$...\$
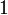
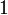
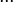
2. Differenzfolge:			$1\$		$1\$		$1\$		$...\$

Arithmetische Folgen g-ter Ordnung sind genau diejenigen Folgen, die sich durch ein Polynom g-ten Grades beschreiben lassen.

Folgen auf Basis der Potenzfunktion

Eine Potenzfolge ist eine Folge, für die die Potenzfunktion die Glieder liefert (Erzeugende Funktion)

Die Folge der Quadratzahlen: 0, 1, 4, 9, ... hat die Funktionsvorschrift a_i = i². Die Folge der Quadratzahlen ist ebenfalls eine arithmetische Folge 2. Ordnung, da sie sich als Reihe auffassen lässt, der die Folge der ungeraden Zahlen zugrunde liegt.

Die Folge der Kubikzahlen 0, 1, 8, 27, ... besitzt die Vorschrift

a_i = i³,

was man für s-te Potenzen der natürlichen Zahlen zu

a_i = i^s

verallgemeinern kann, wobei s eine beliebige reelle Zahl sein darf. Mit s = 1 / 2 erhält man die Folge 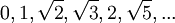$0, 1, \sqrt{2}, \sqrt{3}, 2, \sqrt{5},...$ der Quadratwurzeln der natürlichen Zahlen,

$a_i = i^{0,5} = \sqrt i$.

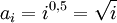Bei negativen Exponenten s < 0 ist zu beachten, dass 0^s nicht existiert. Beispielsweise ist es nicht möglich, mit s = − 1 und der Funktionsvorschrift

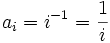$a_i = i^{-1} = \frac{1}{i}$ das Folgenglied zum Index i = 0

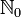zu berechnen. Man kann den Index 0 ausschließen, sich also auf die Indexmenge $\N^+$ beschränken. Oft ist es jedoch zweckmäßiger, die Indexmenge $\N_0$ unverändert zu lassen und stattdessen die Funktionsvorschrift in

$a_i = (i+1)^{-1} = \frac{1}{i+1}$

abzuändern. Dann lauten die ersten Folgenglieder 1, 1/2, 1/3, 1/4, ... In gleicher Weise kann man eine Funktionsvorschrift für beliebige Exponenten s aufstellen:

a_i = (i + 1)^s.

Geometrische Folgen

So wie in einer arithmetischen Folge aufeinanderfolgende Glieder eine konstante Differenz haben, so stehen in einer geometrische Folge

$a_i = a_0 \cdot q^i$

aufeinanderfolgende Glieder in einem konstanten Verhältnis zueinander, a_{i + 1} / a_i = q. Zum Beispiel ergibt sich mit q = 2 die Folge der Zweierpotenzen

a_i = 2ⁱ,

also zum Beispiel für die ersten zehn Glieder die Folge 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 (jedes Glied ist doppelt so groß wie das vorangegangene). Wichtig ist diese Folge speziell für die Umwandlung von den in der Informatik verwendeten Dualzahlen in Dezimalzahlen (und umgekehrt). Eine geometrische Folge mit 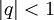$\vert q \vert &amp;lt; 1$ konvergiert gegen Null, wie beispielsweise die Folge 1; 0,1; 0,01; ... zu q = 0,1:

$a_i = \left(\frac{1}{10}\right)^i.$

Wenn q = 1 erhält man die triviale Folge 1, 1, 1, ...; wenn q = − 1, erhält man aus

a_i = ( − 1)ⁱ

die fundamentale alternierende Folge 1, −1, 1, −1, ...

Ein Beispiel für die Alltagsanwendung der geometrischen Folge ist die gleichstufige Stimmung der musikalischen Tonleiter – die aufeinanderfolgenden Glieder, hier Halbtonschritte, besitzen zueinander ein konstantes Frequenzverhältnis.

Verallgemeinerungen

In der Topologie ist ein Netz eine Verallgemeinerung einer Folge.

Ebenso wie bei Funktionen kann man neben den hier definierten Folgen mit Werten in Mengen auch Folgen mit Werten in einer echten Klasse definieren, also beispielsweise Folgen von Mengen oder Gruppen.

Literatur

• Bourbaki: Elements de Mathematique, Theorie des Ensembles, II,III Paris 1970
• Harro Heuser: Lehrbuch der Analysis, Teil 1, Teubner Verlag, Stuttgart

Weblinks

• Online-Enzyklopädie der Zahlenfolgen
• Zahlenfolgen für Schüler erklärt
• Folgen und Tupel in der Encyclopaedia of Mathematics, Springer, Edited by Michiel Hazewinkel