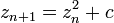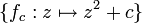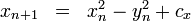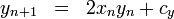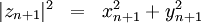Mandelbrotmenge

Die Mandelbrot-Menge, im allgemeinen Sprachgebrauch oft auch Apfelmännchen genannt, ist eine fraktal erscheinende Menge, die in der Chaostheorie, und genauer in der komplexen Dynamik, eine bedeutende Rolle spielt. Sie wurde 1980 von Benoît Mandelbrot popularisiert und von Adrien Douady und John Hubbard in einer Reihe grundlegender mathematischer Arbeiten systematisch untersucht. (Die ersten computergrafischen Darstellungen wurden 1978 von Brooks und Matelski vorgestellt.) Die mathematischen Grundlagen dafür wurden bereits 1905 von dem französischen Mathematiker Pierre Fatou erarbeitet. (Strenggenommen und im Gegensatz zu häufig zu lesenden Meinungen ist die Mandelbrot-Menge kein Fraktal, denn sie ist nicht selbstähnlich: im Prinzip kann man jeder Ausschnittvergrößerung jedes Randes bei genügender Auflösung ansehen, von welchem Punkt sie stammen!)

Außerhalb der Fachwelt wurde die Mandelbrot-Menge vor allem durch den hohen ästhetischen Reiz dieser Computergrafiken bekannt, der durch bewusste Farbgestaltung des Außenbereichs, der nicht zur Menge gehört, noch erhöht wird. Die Mandelbrot-Menge wird als das formenreichste geometrische Gebilde bezeichnet. Dieser Formenreichtum zeigt sich an stark vergrößerten Ausschnitten des Randes, die überdies Beispiele für das Konzept der Selbstähnlichkeit bei Fraktalen liefern. Trotz der hohen inneren Ordnung wurde die Mandelbrot-Menge zum Symbol für das mathematische Chaos, welches sich allerdings von Chaos im umgangssprachlichen Sinne grundsätzlich unterscheidet.

Die Bezeichnung „Apfelmännchen“ korrespondiert mit der geometrischen Grobform einer um 90 Grad im Uhrzeigersinn gedrehten Mandelbrotmenge. Möglicherweise hat auch die Bezeichnung APPLEMAN für ein frühes Programm auf einem Apple-Computer zur Verbreitung dieser Bezeichnung beigetragen. Dabei standen im Rahmen eines Wortspiels APPLE für die Computermarke und MAN für eine Abkürzung von „Mandelbrot“.

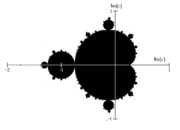
Mandelbrot-Menge (schwarz) mit farbig dargestellter Umgebung. Jedem Pixel ist eine bestimmte Zahlenfolge zugeordnet. Der Folgenindex, ab dem alle Folgenglieder einen Betrag größer als 1000 haben, wächst von Farbstreifen zu Farbstreifen zur Mandelbrot-Menge hin um den Wert 1.

Definition

Die Mandelbrot-Menge (schwarz) in der komplexen Ebene

Definition über Rekursion

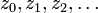Die Mandelbrot-Menge $\Bbb M$ ist die Menge aller komplexen Zahlen c, für welche die rekursiv definierte Folge komplexer Zahlen $z_0, z_1, z_2, \ldots$ mit dem Bildungsgesetz

$z_{n+1} = z_n^2 + c$

und dem Anfangsglied

z₀ = 0

beschränkt bleibt, das heißt, der Betrag der Folgenglieder wächst nicht über alle Grenzen. Die grafische Darstellung dieser Menge erfolgt in der komplexen Ebene. Die Punkte der Menge werden dabei in der Regel schwarz dargestellt und der Rest farbig, wobei die Farbe eines Punktes den Grad der Divergenz der zugehörigen Folge widerspiegelt (siehe unten).

Definition über Julia-Mengen

Die Mandelbrot-Menge $\Bbb M$ wurde von Benoît Mandelbrot ursprünglich zur Klassifizierung von Julia-Mengen eingeführt, die bereits Anfang des 20. Jahrhunderts von den französischen Mathematikern Gaston Maurice Julia und Pierre Fatou untersucht wurden. Die Julia-Menge J_c zu einer bestimmten komplexen Zahl c ist definiert als der Rand der Menge aller Anfangswerte z₀, für die die obige Zahlenfolge beschränkt bleibt. Man kann beweisen, dass die Mandelbrot-Menge $\Bbb M$ genau die Menge der Werte c ist, für die die zugehörige Julia-Menge J_c zusammenhängend ist.

Verallgemeinerte Mandelbrot-Mengen

Im allgemeinen Sprachgebrauch wird die oben definierte Menge $\Bbb M$ als die Mandelbrot-Menge bezeichnet. Verwendet man anstelle des obigen Bildungsgesetzes die Rekursionsregel

z_{n + 1} = f_c(z_n)

mit einer von einem komplexen Parameter c abhängigen Abbildung f_c innerhalb der komplexen Zahlen, so lässt sich in analoger Weise eine zu dieser Abbildung gehörige Mandelbrot-Menge und entsprechende Julia-Mengen definieren. Der Startwert z₀ muss ein kritischer Punkt sein, das heißt, es muss f_c'(z₀) = 0 gelten.

Dieses Verfahren kann auch für Funktionen mit mehr als einem komplexen Parameter c erweitert werden. Allerdings ist dann eine grafische Darstellung in zwei Dimensionen ohne Projektion nicht mehr möglich.

Die folgenden Ausführungen beziehen sich nur auf die üblicherweise betrachtete Mandelbrot-Menge.

Geometrische und mathematische Eigenschaften

Video: Zoom in eine Mandelbrot-Menge

Der ungeheure Formenreichtum der Mandelbrot-Menge erschließt sich aus ihrem Bezug zu Julia-Mengen. Julia-Mengen zur Iteration z→z²+c sind Fraktale, außer für einige c-Werte wie c=−2 (Strecke) oder c=0 (Kreis). Die Formen dieser fraktalen Strukturen sind innerhalb einer Julia-Menge stets die gleichen, umspannen aber für Julia-Mengen zu verschiedem Parameter c einen enormen Formenreichtum. Es zeigt sich, dass die Strukturen der Mandelbrot-Menge in der Umgebung eines bestimmten Wertes c genau jene Strukturen der zugehörigen Julia-Menge J_c wiedergeben. Damit enthält die Mandelbrot-Menge den kompletten Formenreichtum der unendlich vielen Julia-Mengen (s. u.).

In den fraktalen Strukturen am Rand findet man verkleinerte ungefähre Kopien der gesamten Mandelbrot-Menge, so genannte Satelliten. Jeder Bildausschnitt der Mandelbrot-Menge, der sowohl Punkte aus $\Bbb M$ als auch solche außerhalb $\Bbb M$ umfasst, enthält unendlich viele dieser Satelliten. Unmittelbar am Rand eines Satelliten treten fast die gleichen Strukturen auf wie an den entsprechenden Stellen des Originals. Diese Strukturen sind jedoch nach weiter außen hin mit den Strukturen kombiniert, die für die größere Umgebung des Satelliten typisch sind. Diese Situation wird gelegentlich mit der eines biologischen Organismus und seiner Gene verglichen. Danach entspricht jedem Satelliten die Erbsubstanz einer Zelle, die den Bauplan für den kompletten Organismus enthält, während nach außen hin nur die Strukturen des lokalen Organs exprimiert sind. Es handelt sich dabei jedoch um ein rein formales Gleichnis ohne kausalen Hintergrund.

Da jeder Satellit wiederum mit Satelliten höherer Ordnung bestückt ist, lässt sich immer eine Stelle finden, an der eine beliebige Anzahl beliebiger verschiedener Strukturen in beliebiger Reihenfolge kombiniert auftritt. Diese Strukturen sind dann allerdings nur bei extremer Vergrößerung erkennbar.

Die Mandelbrot-Menge ist spiegelsymmetrisch zur reellen Achse. Sie ist zusammenhängend (das heißt, sie bildet keine Inseln) und voll (sie hat also keine Löcher). (Ob M einfach zusammenhängend ist, ist nicht bekannt, denn es ist nicht einmal bekannt, ob M wegzusammenhängend ist.) Die Mandelbrotmenge ist nicht selbstähnlich, denn keine zwei Teilstrukturen ihres Randes sind exakt gleich; aber in der Nähe vieler Randpunkte bilden sich bei fortgesetzter Ausschnittvergrößerung im Grenzwert periodische Strukturen.

Da die Mandelbrot-Menge Kardioid- und Kreisflächen enthält, hat sie die fraktale Dimension zwei. Der Rand der Mandelbrot-Menge hat eine unendliche Länge, und seine Hausdorff-Dimension beträgt nach Arbeiten von Mitsuhiro Shishikura ebenfalls zwei; das impliziert, dass auch die Box-Dimension den Wert 2 hat. Es ist denkbar, dass der Rand der Mandelbrotmenge einen positiven (notwendig endlichen) Flächeninhalt hat; andernfalls wäre dieser Flächeninhalt null. Der Flächeninhalt der Mandelbrot-Menge ist nicht bekannt und beträgt nach numerischen Schätzungen etwa 1,506 591 77. Einer Spekulation zufolge beträgt der exakte Wert 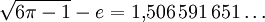$\sqrt{6\pi -1} - e = 1{,}506\,591\,651 \ldots$ ^[1].

Die Frage, ob die Mandelbrotmenge entscheidbar ist, gibt zunächst keinen Sinn, da $\Bbb M$ überabzählbar ist. Ein Ansatz, den Begriff der Entscheidbarkeit auf überabzählbare Mengen zu verallgemeinern, stellt das Blum-Shub-Smale-Modell dar. Innerhalb dessen ist die Mandelbrotmenge nicht entscheidbar.

Bildergalerie einer Zoomfahrt

Die folgende exemplarische Bildersequenz einer Zoomfahrt an eine bestimmte Stelle c gibt einen Eindruck vom geometrischen Formenreichtum und erläutert gewisse typische Strukturelemente. Die Vergrößerung im letzten Bild beträgt etwa 1 zu 60 Milliarden. Bezogen auf einen üblichen Computerbildschirm verhält sich dieser Ausschnitt wie zu der Gesamtgröße des Apfelmännchens von 2,5 Millionen Kilometern, dessen Rand in dieser Auflösung eine unvorstellbare Fülle verschiedenster fraktaler Strukturen aufweist.

Startbild	Ausschnitt 1	Ausschnitt 2	Ausschnitt 3	Ausschnitt 4
Ausschnitt 5	Ausschnitt 6	Ausschnitt 7	Ausschnitt 8	Ausschnitt 9
Ausschnitt 10	Ausschnitt 11	Ausschnitt 12	Ausschnitt 13	Ausschnitt 14

Bildnummer	Beschreibung
Startbild	Die Mandelbrot-Menge mit stufenlos eingefärbtem Außenraum.
Ausschnitt 1	Spalte zwischen „Kopf“ und „Körper“, auch „Tal der Seepferdchen“ genannt.
Ausschnitt 2	Links Doppelspiralen, rechts „Seepferdchen“.
Ausschnitt 3	„Seepferdchen“. Der „Körper“ wird von 25 „Speichen“ gebildet, von denen sich zwei Zwölfergruppen nach Art einer Metamorphose auf jeweils einen der beiden „Finger“ an der „oberen Hand“ des Apfelmännchens zurückführen lassen. Die Zahl der „Speichen“ nimmt daher von einem „Seepferdchen“ zum nächsten um zwei zu. Die „Nabe“ wird von einem Misiurewicz-Punkt gebildet (s. u.). Zwischen „Oberkörper“ und „Schwanz“ ist ein deformierter Satellit erkennbar.
Ausschnitt 4	Der „Seepferdchenschwanz“ endet ebenfalls in einen Misiurewicz-Punkt.
Ausschnitt 5	Teil des „Schwanzes“. Der einzige Pfad, der sich durch den gesamten „Schwanz“ windet, und damit gewährleistet, dass $\Bbb M$ einfach zusammenhängend ist, führt im Zickzack von einer „Schwanzseite“ zur anderen und passiert dabei die „Naben“ der großen 25-spiraligen Gebilde.
Ausschnitt 6	Satellit. Die beiden „Seepferdchenschwänze“ bilden den Auftakt für eine Folge von konzentrischen Kränzen mit dem Satelliten im Zentrum.
Ausschnitt 7	Jeder dieser Kränze besteht aus gleichartigen Strukturelemente, deren Anzahl pro Kranz mit Potenzen von 2 wächst, ein typisches Phänomen in der Umgebung von Satelliten. Der oben erwähnte Pfad durch den „Seepferdchenschwanz“ passiert den Satelliten über die Kerbe der Kardioide und die Spitze der „Antenne“ auf dem „Kopf“.
Ausschnitt 8	„Antenne“ des Satelliten. Auf ihr sind mehrere Satelliten 2. Ordnung erkennbar.
Ausschnitt 9	„Tal der Seepferdchen“ des Satelliten. Es zeigen sich die gleichen Strukturelemente wie in Ausschnitt 1.
Ausschnitt 10	Doppelspiralen und „Seepferdchen“, die jedoch im Unterschied zu Ausschnitt 2 nach außen hin mit seepferdchenschwanzartigen Fortsätzen bestückt sind. Dieses Phänomen demonstriert die für Satelliten n-ter Ordnung typischen Verkettungen von n+1 Strukturelementen für den Fall n=1.
Ausschnitt 11	Doppelspiralen mit Satelliten 2. Ordnung. Sie lassen sich als Metamorphose der „Antenne“ interpretieren.
Ausschnitt 12	Im Bereich der äußeren Fortsätze sind stets inselartige Strukturen eingestreut, die Julia-Mengen Jc ähneln. Die im Bild größte ist im Zentrum des „Doppelhakens“ rechts gerade eben erkennbar.
Ausschnitt 13	Teil des „Doppelhakens“.
Ausschnitt 14	Diese Inseln scheinen auf den ersten Blick nach Art von Cantor-Mengen wiederum aus unendlich vielen unzusammenhängenden Teilstücken zu bestehen, wie es für die zugehörigen Jc tatsächlich der Fall ist, sie sind jedoch hier über filigrane Strukturen miteinander verbunden. Diese Strukturen gehen von einem Satelliten im Zentrum aus, der bei dieser Vergrößerung noch nicht sichtbar ist, und zwar derart, dass das Ganze ein einfach zusammenhängendes Gebilde ergibt. Der zum entsprechenden Jc gehörige c-Wert ist nicht der des Bildzentrums sondern hat relativ zum Hauptapfelmännchen die gleiche Position wie das Bildzentrum zum Satelliten, der in Ausschnitt 7 dargestellt ist.

Eine Animation zu dieser Zoomfahrt findet sich bei den Weblinks.

Verhalten der Zahlenfolge

Die verschiedenen Strukturelemente von $\Bbb M$ stehen in engem Zusammenhang mit bestimmten Verhaltensweisen der Zahlenfolge, die $\Bbb M$ zugrunde liegt. Je nach Wert von c ergibt sich eine der folgenden vier Möglichkeiten:

• Sie strebt gegen einen festen Wert (Konvergenz).
• Sie konvergiert gegen einen periodischen Grenzzyklus, der aus 2 oder mehr Zahlen besteht.
• Sie wiederholt sich nie, bleibt aber beschränkt (für manche dieser Parameter ergibt sich chaotisches Verhalten).
• Sie strebt gegen Unendlich (bestimmte Divergenz).

Alle c-Werte, die zu den ersten drei Verhaltensweisen führen, gehören zu $\Bbb M$.

Geometrische Zuordnung

Konvergenz liegt genau für die Werte von c vor, die das Innere der Kardioide bilden, den „Körper“ des Apfelmännchens, sowie für abzählbar viele ihrer Randpunkte. Periodische Grenzzyklen findet man in den (angenähert) kreisförmigen „Knospen“ wie z. B. im „Kopf“, in den Kardioiden der Satelliten, sowie ebenfalls auf abzählbar vielen Randpunkten dieser Komponenten. Eine fundamentale Vermutung besagt, dass es für alle inneren Punkte der Mandelbrotmenge einen Grenzzyklus gibt. Die Folge ist echt vorperiodisch für abzählbar viele Parameter, die oft Misiurewicz-Thurston-Punkte genannt werden. Dazu gehören die „Antennenspitzen“, wie z. B. Punkt z=-2 ganz links, und Verzweigungspunkte der Mandelbrotmenge.

In den überabzählbar vielen übrigen Punkten der Mandelbrotmenge kann sich die Folge auf viele verschiedene Weisen verhalten, die jeweils sehr unterschiedliche dynamische Systeme erzeugen, und die teilweise Gegenstand intensiver Forschung sind. Je nach Definition des Wortes kann man „chaotisches“ Verhalten finden.

Periodisches Verhalten

Die kreisförmigen Strukturen

Mandelbrotmenge mit farbig dargestellter Periodenlänge der Grenzzyklen

Jede kreisförmige „Knospe“ und jede Satelliten-Kardioide zeichnet sich durch eine bestimmte Periodizität des Grenzzyklus aus, gegen den die Folge für die zugehörigen c-Werte strebt. Die Anordnung der „Knospen“ an der zugehörigen Kardioide folgt dabei den folgenden Regeln, aus denen sich unmittelbar die Periodizitäten ablesen lassen. Jede „Knospe“ berührt genau einen Basiskörper, nämlich eine größere „Knospe“ oder eine Kardioide.

Die Periodizität einer „Knospe“ ist die Summe der Periodizitäten der beiden nächsten größeren „Nachbarknospen“ in beide Richtungen am selben Basiskörper, sofern es solche gibt. Gibt es am Rand des Basiskörpers bis zur Kontaktstelle mit dessen Basiskörper bzw. bis zur Kerbe der Kardioide nur kleinere „Knospen“, so trägt anstelle der Periodizität einer „Nachbarknospe“ die des Basiskörpers selbst zur Summe bei. Daraus leiten sich unmittelbar die folgenden Eigenschaften ab:

• Tendenziell sind die „Knospen“ bzw. Kardioiden umso kleiner, je größer ihre Periodizität ist.
• Die Periodizität der größten „Knospe“ an einem Basiskörper beträgt stets das doppelte, wie beispielsweise der „Dutt“ mit der Periode 4 am „Kopf“.
• Die Periodizität einer „Knospe“ eines Satelliten ist das Produkt der Periodizität der Kardioide und der der korrespondierenden „Knospe“ der Hauptkardioide.

Ferner erklärt diese Regel das Auftreten bestimmter Folgen von „Knospen“ wie beispielsweise vom „Kopf“ zur Kardioidkerbe hin mit einer Periodizitätszunahme zur nächsten „Knospe“ hin um den Wert 1 oder vom „Arm“ zum „Kopf“ hin um den Wert 2.

Attraktive Zyklen

Gibt es für ein c ein Folgenglied mit der Eigenschaft z_n=z₀=0, so wiederholt sich die Folge von Anfang an streng periodisch und zwar mit der Periode n. Da sich z_n durch n-malige Anwendung der Iterationsvorschrift ergibt, wobei bei jedem Schritt quadriert wird, lässt es sich als Polynom von c vom Grad 2^n-1 formulieren. Die c-Werte für periodische Folgen der Periode n erhält man daher über die 2^n-1 Nullstellen dieses Polynoms. Es zeigt sich, dass jede Zahlenfolge gegen diesen Zahlenzyklus konvergiert, sofern eins ihrer Folgenglieder hinreichend nahe an diesen Zyklus gerät. Man spricht von sogenannten Attraktoren.

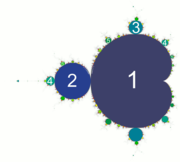
Das führt dazu, dass auch alle Zahlenfolgen zu einer gewissen Umgebung des c-Wertes, der den Attraktor repräsentiert, gegen einen stabilen Zyklus der Periode n konvergieren. Jede kreisförmige „Knospe“ und jede Kardioide eines Satelliten repräsentiert genau eine solche Umgebung. Exemplarisch seien die Gebiete mit den Perioden 1 bis 3 aufgeführt:

• Periode 1: Die Kardioide des Hauptapfelmännchens
• Periode 2: Der „Kopf“. Die 2. Nullstelle c=0 entspricht der Hauptkardioide, die wegen der Periode 1 natürlich auch bei der Ermittlung aller höherer Perioden als Nullstelle auftritt. Diese Überlegung zeigt, dass die Zahl der Attraktoren mit der Periode n (>1) maximal 2^n-1-1 betragen kann, und das auch nur dann, wenn n eine Primzahl ist.
• Periode 3: Die „Knospen“, die den „Armen“ entsprechen und die Kardioide des größten Satelliten auf der „Kopfantenne“. Die 4. Nullstelle c=0 entfällt wieder.

Die Anzahl der anziehenden Zyklen mit der genauen Periode n, d.h. z_n=z₀ und n ist minimal mit dieser Eigenschaft, ist die Folge A000740 in OEIS.

Galerie der Iteration

Die folgende Galerie gibt einen Überblick über die Werte von z_n für einige Werte von n. Dabei hängt z_n vom Parameter c ab, dessen Realteil sich in den Bildern von links nach rechts von −2.2 bis 1 erstreckt, und dessen Imaginärteil von −1.4 bis 1.4 reicht.

Die Iteration z → z²+c nach n Schritten

n = 1	n = 2	n = 3	n = 4
n = 5	n = 9	n = 17	n = 18

Iterationen	Beschreibung
n = 1	Nach dem ersten Schritt gilt z1(c) = c. Das Bild ist also eine farbige Darstellung der komplexen Zahlen c, welche sich in dem gezeigten Gebiet befinden. Die Null wird dabei in Weiß dargestellt und Unendlich in Schwarz. Daher erscheint ein Punkt umso dunkler, je weiter er vom Ursprung entfernt ist. Die Farbe eines Punktes gibt Auskunft über sein Argument, also über den Winkel, den er mit der positiv-reellen Achse (rot) hat.
n = 2	Nach zwei Schritten gilt z2(c) = c2 + c = c·(c + 1) Dieser Ausdruck wird Null für c = 0 sowie für c = −1. Die neu hinzugekommene linke Nullstelle liegt im Zentrum des Kopfes des Apfelmännchens, während die alte auf der rechten Seite das Herz der Leib-Zykloiden ist.
n = 3	Die Anzahl der Nullstellen hat sich verdoppelt — wie nach jedem Iterationsschritt. An der reellen Nullstelle links sieht man den der kleinen Antennen-Satellit knospen. Es treten die ersten komplexwertigen Nullstellen ober- und unterhalb der reellen Achse auf. Diese Nullstellen liegen genau dort, wo die Ärmchen entstehen.
n = 4	Der Dutt ist entstanden. Die dargestellte Funktion z4(c) = (((c2 + c)2 + c)2 + c)2 + c wird immer unübersichtlicher. Es lässt sich jedoch einfach nachrechnen, dass wenn co eine Nullstelle von zn ist, co auch eine Nullstelle von zk·n ist. Daher „erbt“ z4 die Nullstellen von z2. Dieser Zusammenhang ist Ursache für das unten erläuterte periodische Verhalten der Knospen.
n = 5	Da 5 eine Primzahl ist, gibt es keine altbekannten Nullstellen — außer der null, welche von z1 bekannt ist. Da der Grad des Polynoms zn(c) gleich 2n−1 ist, wächst zn mit wachsendem n immer schneller gegen Unendlich. Dadurch bildet sich der Rand zwischen der Mandelbrotmenge und ihrem Äußeren immer klarer heraus.
n = 9	Inzwischen gibt es bereits 256 Nullstellen, die munter innerhalb des Apfelmännchens verteilt sind. Da 3 ein Teiler von 9 ist, sind die Arm-Knospen wieder mit einer Nullstelle an der Reihe, und leuchten daher hell auf.
n = 17	Wieder eine Primzahl
n = 18	Mit n = 18 und 217 = 131072 Nullstellen endet diese Bilderserie, n könnte man noch beliebig vergrößern, womit sich auch die Anzahl der neuen Knospen erhöht.

Repulsive Zyklen

Neben attraktiven Zyklen gibt es auch repulsive, die sich dadurch auszeichnen, dass Zahlenfolgen in ihrer Umgebung sich zunehmend von ihnen entfernen. Sie lassen sich jedoch erreichen, da jedes z_n abgesehen von der Situation z_n-1=0 wegen des Quadrats in der Iterationsvorschrift zwei potenzielle Vorgänger in der Folge hat, die sich nur durch ihr Vorzeichen unterscheiden. c-Werte, für die die zugehörige Folge irgendwann über einen solchen zweiten Vorläufer eines Periodenmitgliedes in einen derartigen instabilen Zyklus mündet, sind beispielsweise die „Naben“ der rad- bzw. spiralförmigen Strukturen sowie die Endpunkte der weitverbreiteten antennenartigen Strukturen, die sich formal als „Naben“ von „Rädern“ oder Spiralen mit einer einzigen Speiche interpretieren lassen. Derartige c-Werte werden auch als Misiurewicz-Punkte bezeichnet.

Ein Misiurewicz-Punkt c hat ferner die Eigenschaft, dass $\Bbb M$ in seiner näheren Umgebung nahezu deckungsgleich mit demselben Ausschnitt der zugehörige Julia-Menge J_c ist. Je weiter man sich dem Misiurewicz-Punkt nähert, umso besser wird die Übereinstimmung. Da Julia-Mengen für c-Werte innerhalb von $\Bbb M$ zusammenhängend sind und außerhalb von $\Bbb M$ Cantor-Mengen aus unendlich vielen Inseln mit der Gesamtfläche Null, sind sie in der Übergangszone am Rand von $\Bbb M$ besonders filigran. Jeder Misiurewicz-Punkt ist aber gerade ein Randpunkt von $\Bbb M$, und jeder Ausschnitt der Randzone von $\Bbb M$, der sowohl Punkte in $\Bbb M$ als auch außerhalb davon enthält, enthält unendlich viele davon. Damit ist der gesamte Formenreichtum sämtlicher Julia-Mengen dieses filigranen Typs in der Umgebung der Misiurewicz-Punkte in $\Bbb M$ repräsentiert.

Satelliten

Ein weiteres Strukturelement, das den Formenreichtum der Mandelbrotmenge begründet, sind die verkleinerten Kopien ihrer selbst, die sich in den filigranen Strukturen ihres Randes befinden. Dabei korrespondiert das Verhalten der Zahlenfolgen innerhalb eines Satelliten in folgender Weise mit dem der Folgen im Hauptkörper. Innerhalb eines Satelliten konvergieren alle Zahlenfolgen gegen Grenzzyklen, deren Perioden sich von denen an den entsprechenden Stellen im Hauptkörper von $\Bbb M$ um einen Faktor p unterscheiden. Betrachtet man für einen bestimmten c-Wert aus dem Satelliten nur jedes p-te Folgenglied, so ergibt sich eine Folge, die bis auf einen räumlichen Maßstabsfaktor nahezu identisch ist mit derjenigen, die sich für den entsprechenden c-Wert im Hauptkörper von $\Bbb M$ ergibt. Die mathematische Begründung hierfür ist tiefliegend; sie entstammt den Arbeiten von Douady und Hubbard über „polynomartige Abbildungen“.

Die zusätzlichen Strukturelemente in der unmittelbaren Umgebung eines Satelliten sind eine Folge davon, dass zwischen zwei der betrachteten Folgenglieder mit dem Indexabstand p sich eins mit dem Wert z_n=0 befinden kann, das damit einen periodischen Verlauf mit der Periode n begründet. Die entsprechende Folge außerhalb des Hauptkörper divergiert jedoch, da sie keine solchen Zwischenglieder besitzt.

Analyse des Verhaltens des Newton-Verfahrens zu einer Familie kubischer Polynome

Es handelt sich bei der Mandelbrot-Menge selbst um eine universelle Struktur, die auch bei völlig anderen nichtlinearen Systemen und Klassifizierungsregeln in Erscheinung treten kann. Grundvoraussetzung ist jedoch, dass die beteiligten Funktionen winkeltreu sind. Betrachtet man solche Systeme, die von einem komplexen Parameter c abhängen und klassifiziert ihr Verhalten bezüglich einer bestimmten Eigenschaft der Dynamik in Abhängigkeit von c, dann findet man unter bestimmten Umständen in der Parameter-Ebene kleine Kopien der Mandelbrot-Menge. Ein Beispiel ist die Frage, für welche Polynome dritten Grades das iterative Newton-Verfahren zur Bestimmung von Nullstellen mit einem bestimmten Startwert versagt und für welche nicht.

Wie im nebenstehenden Bild kann die Mandelbrot-Menge dabei verzerrt auftreten, zum Beispiel sitzen dort die Armknospen an etwas anderer Stelle. Ansonsten ist die Mandelbrot-Menge jedoch vollkommen intakt, inklusive aller Knospen, Satelliten, Filamente und Antennen. Der Grund für das Auftauchen der Mandelbrot-Menge ist, dass die betrachtete Funktionenfamilien in bestimmten Gebieten – abgesehen von Drehungen und Verschiebungen – recht gut mit der Funktionenfamile

$\{f_c : z\mapsto z^2+c\}$

welche die Mandelbrot-Menge definiert, übereinstimmen. Dabei sind in einem gewissen Rahmen Abweichungen zulässig, und trotzdem kristallisiert sich die Mandelbrot-Menge heraus. Dieses Phänomen wird auch als strukturelle Stabilität bezeichnet und ist im Endeffekt auch verantwortlich für das Auftreten der Satelliten in der Umgebung von $\Bbb M$, weil Teilfolgen der iterierten Funktionen lokal das gleiche Verhalten zeigen wie die Gesamtfamilie.

Intermediär wechselhaftes Verhalten

Darstellung des Betrages der Folgenglieder als Funktion des Iterationsschrittes n für einen c-Wert mit besonders abwechslungsreichem Verhalten der Folge. Die auffälligen Brüche im Verhalten ergeben sich durch Beinahe-Einfänge in repulsive Zyklen, was temporär zu quasiperiodischem Verhalten führt.

Darstellung der Folgenglieder zum c-Wert des vorherigen Diagramms als Punkte in der komplexen Ebene mit hinterlegter Mandelbrotmenge zur Orientierung. Die Helligkeit eines Pixels ist ein Maß dafür, von wie vielen Punkten der Folge es getroffen wurde.

Durch die Möglichkeit der Zahlenfolge, wiederholt in die unmittelbaren Umgebung eines repulsiven Zyklus zu geraten, und bei dem anschließend tendenziell divergenten oder chaotischen Verhalten wiederum beinahe in einen anderen Zyklus zu geraten, können sich intermediär sehr komplizierte Verhaltensweisen der Folge ausbilden, bis sich der endgültige Charakter der Folge zeigt, wie die beiden Abbildungen demonstrieren. Die Umgebung der zugehörigen c-Werte in $\Bbb M$ ist entsprechend strukturreich.

Auch die Darstellung der Folgepunkte selbst in der komplexen Ebene zeigt in diesen Fällen eine größere Komplexität. Das quasiperiodische Verhalten in der Nachbarschaft eines repulsiven Zyklus führt in diesen Fällen oft zu spiralförmigen Strukturen mit mehreren Armen, wobei die Folgepunkte das Zentrum umkreisen, während der Abstand zu ihm zunimmt. Die Anzahl der Arme entspricht daher der Periode. Die Punktanhäufungen an den Enden den Spiralarme in der obigen Abbildung sind die Folge der beiden zugehörigen Beinahe-Einfänge durch repulsive (instabile) Zyklen.

Dichteverteilung der Folgenglieder

Summarische Dichteverteilung der Folgenglieder für alle c-Werte in einer farbkodierten Darstellung

Grenzzyklen für reelle c-Werte. Konvergenz geht über Bifurkation in Chaos über

Zusammenhang zwischen der Mandelbrotmenge und der logistischen Gleichung

Das nebenstehende Bild zeigt in der komplexen Ebene die Dichteverteilung der Folgenglieder, die man erhält, wenn man alle Folgen für c-Werte auf einem engen flächendeckenden Raster berücksichtigt. Im großen Kreis entspricht das der Dichteverteilung der Endpunkte der konvergenten Folgen zu c-Werten aus der Kardioide. Die beiden nächstkleineren Gebilde markieren die Bereiche zwischen denen die Grenzzyklen mit der Periode 2 für Folgen zu c-Werten aus dem „Kopf“ hin und her springen. Die gitterförmigen Linien sind Artefakte als Folge eines Moiré-Effekts zwischen dem Raster der c-Werte und dem für die numerische Auswertung der Dichteverteilung.

Bezug zur Chaostheorie

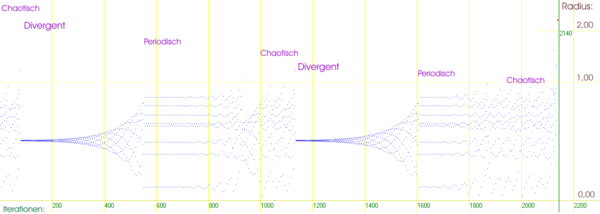
Das Bildungsgesetz, das der Folge zugrunde liegt, ist die einfachste nichtlineare Gleichung, anhand der sich der Übergang von Ordnung zu Chaos durch Variation eines Parameters provozieren lässt. Dazu genügt es, reelle Zahlenfolgen zu betrachten.

Man erhält sie, wenn man sich auf die c-Werte der x-Achse von $\Bbb M$ beschränkt. Für Werte –0,75<=c<=0,25, das heißt innerhalb der Kardioide, konvergiert die Folge. Auf der „Antenne“, die bis c=-2 reicht, verhält sich die Folge chaotisch. Der Übergang zu chaotischem Verhalten erfolgt nun über ein Zwischenstadium mit periodischen Grenzzyklen. Dabei nimmt die Periode zum chaotischen Bereich hin stufenweise um den Faktor zwei zu, ein Phänomen, das als Periodenverdopplung und Bifurkation bezeichnet wird. Jeder c-Bereich zu einer bestimmten Periode entspricht dabei einer der kreisförmigen „Knospen“ auf der x-Achse.

Die Periodenverdopplung beginnt mit dem „Kopf“ und setzt sich in der Folge der „Knospen“ zur „Antenne“ hin fort. Das Verhältnis der Längen aufeinander folgender Parameterintervalle und damit das der Knospendurchmesser zu unterschiedlicher Periode strebt dabei gegen die Feigenbaum-Konstante δ ≈ 4,669, eine fundamentale Konstante der Chaostheorie. Dieses Verhalten ist typisch für den Übergang realer Systeme zu chaotischer Dynamik. Die auffälligen Lücken im chaotischen Bereich entsprechen Inseln mit periodischem Verhalten, denen in der komplexen Ebene die Satelliten auf der „Antenne“ zugeordnet sind.

Für gewisse komplexe c-Werte stellen sich Grenzzyklen ein, die auf einer geschlossenen Kurve liegen, deren Punkte jedoch nicht periodisch sondern chaotisch abgedeckt werden. Eine solche Kurve ist in der Chaostheorie als sogenannter seltsamer Attraktor bekannt.

Die Mandelbrot-Menge ist daher ein elementares Objekt für die Chaostheorie, an der sich fundamentale Phänomene studieren lassen. Sie wird aus diesem Grund hinsichtlich ihrer Bedeutung für die Chaostheorie gelegentlich mit der von Geraden für die euklidische Geometrie verglichen.

Grafische Darstellung

Die grafische Darstellung der Mandelbrot-Menge und ihrer Strukturen im Randbereich ist nur mittels Computer möglich. Dabei entspricht jedem Bildpunkt ein Wert c der komplexen Ebene. Der Computer ermittelt für jeden Bildpunkt, ob die zugehörige Folge divergiert oder nicht. Sobald der Betrag |z_n| eines Folgengliedes den Wert R=2 überschreitet, divergiert die Folge. Die Zahl der Iterationsschritte N gemäß obiger Rekursionsformel, nach denen das erfolgt, kann als Maß für den Divergenzgrad herangezogen werden. Über eine zuvor festgelegte Farbtabelle, die jedem Wert N eine Farbe zuordnet, wird in diesem Fall dem Bildpunkt eine Farbe zugewiesen. Um in ästhetischer Hinsicht harmonische Grenzen zwischen aufeinanderfolgenden Farben zu erreichen, wird in der Praxis für die Grenze R nicht der kleinste mögliche Wert R=2, sondern ein Wert R≫1 gewählt, da andernfalls die Farbstreifenbreite oszilliert. Für R≫1 bilden die Farbgrenzen darüber hinaus Äquipotenzialflächen, die man erhält, wenn man die Mandelbrot-Menge als elektrisch geladenen Leiter interpretiert. Für kontinuierliche Farbverläufe, wie beispielsweise in der obigen Zoom-Bilderserie, ist eine Auswertung des Faktors erforderlich, um den R bei der ersten Überschreitung übertroffen wurde.

Da die Zahl der Iterationsschritte N, bevor die Grenze R überschritten wird, beliebig groß sein kann, muss für die praktische Durchführung der Rechnung ein Abbruchkriterium in Form einer maximalen Zahl von Iterationsschritten festgelegt werden. Werte von c, deren Folgen danach die Grenze R noch nicht überschritten haben, werden zu $\Bbb M$ gerechnet. Je geringer der Abstand von c zu $\Bbb M$ ist, desto größer ist die Zahl N, nach der R überschritten wird. Je stärker die Vergrößerung ist, mit der man den Rand von $\Bbb M$ darstellen möchte, desto größer muss in diesem Fall die maximalen Zahl von Iterationsschritten gewählt werden, und desto größer fällt auch die Rechenzeit aus. Konvergiert die Folge für einen Startwert c, so kann die Berechnung der Folge auch schon früher abgebrochen werden.

Grafisch besonders reizvoll ist die Darstellung des Randes von $\Bbb M$ mit seinem Formenreichtum. Je stärker die gewählte Vergrößerung ist, umso komplexere Strukturen lassen sich dort finden. Mit entsprechenden Computerprogrammen lässt sich dieser Rand wie mit einem Mikroskop mit beliebiger Vergrößerung darstellen. Die beiden einzigen künstlerischen Freiheiten, die dabei bestehen, sind die Wahl des Bildausschnittes sowie die Zuordnung von Farben zum Divergenzgrad.

Zur Untersuchung interessanter Strukturen sind oft Vergrößerungen erforderlich, die mit der üblichen Rechengenauigkeit gängiger Programmiersprachen aufgrund von Rundungsfehlern nicht darstellbar sind. Manche Programme enthalten daher spezielle Arithmetik-Routinen für 100 Nachkommastellen oder auch deutlich mehr. Die damit erzielbaren Vergrößerungsfaktoren von etwa 10¹⁰⁰ bzw. mehr übersteigen selbst das Verhältnis vom Durchmesser des bekannten Kosmos zu dem eines Protons von nur etwa 10⁴⁰ um einen astronomischen Faktor.

Programmbeispiel

Iteration über alle Bildpunkte

Das folgende Programmbeispiel geht davon aus, dass die Pixel des Ausgabemediums durch Koordinaten pix_x und pix_y mit einem Wertebereich von 1 bis jeweils max_x und max_y adressierbar sind. Die Berechnung des dem Pixel zugeordneten komplexen Zahlenwerts c mit dem Realteil c_x und dem Imaginärteil c_y erfolgt mittels geometrischer Überlegungen.

Die maximale Anzahl von Iterationsschritten ist max_iterationen. Wird dieser Wert überschritten, so wird das entsprechende Pixel der Menge $\Bbb M$ zugeordnet. Der Wert von max_iterationen sollte mindestens 100 betragen. Bei stärkerer Vergrößerung sind zur korrekten Darstellung der Strukturen unter Umständen erheblich größere Werte erforderlich und damit auch deutlich größere Rechenzeiten.

 FOR pix_x = 1 TO max_x
   FOR pix_y = 1 TO max_y

     cx = min_cx + pix_x * punkt_abstand_x
     cy = min_cy + pix_y * punkt_abstand_y

     iterations_wert = punkt_iteration ( cx, cy, max_betrags_quadrat, max_iterationen )

     farb_wert = waehle_farbe ( iterations_wert, max_iterationen )

     plot pix_x pix_y farb_wert

   NEXT pix_y
 NEXT pix_x

Iteration eines Bildpunktes

Die Iteration von n nach n+1 für einen Punkt c der komplexen Zahlenebene erfolgt mittels der komplexen Gleichung

$\begin{matrix} z_{n+1} &amp;amp;amp;=&amp;amp;amp; z_n^2 + c &amp;amp;amp;&amp;amp;amp; \end{matrix}$,

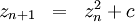die sich mittels der Zerlegung der komplexen Zahl z in ihren Realteil x und Imaginärteil y in zwei reelle Gleichungen

$\begin{matrix} x_{n+1} &amp;amp;amp;=&amp;amp;amp; x_n^2 - y_n^2 + c_x &amp;amp;amp;&amp;amp;amp; \end{matrix}$

und

$\begin{matrix} y_{n+1} &amp;amp;amp;=&amp;amp;amp; 2 x_n y_n + c_y &amp;amp;amp;&amp;amp;amp; \end{matrix}$

umwandeln lässt.

Falls das Quadrat des Betrags der (n+1)-sten Zahl, gegeben durch

$\begin{matrix} |z_{n+1}|^2 &amp;amp;amp;=&amp;amp;amp; x_{n+1}^2 + y_{n+1}^2 &amp;amp;amp;&amp;amp;amp; \end{matrix}$

den Wert max_betrag_quadrat (mindestens 2*2=4) überschreitet, wird die Iteration abgebrochen, und die Anzahl der bislang erfolgten Iterationssschritte für die Zuordnung eines Farbwertes verwendet. Falls das Quadrat des Betrags nach einer gegebenen maximalen Anzahl von Iterationsschritten den max_betrag_quadrat nicht überschritten hat, wird angenommen, dass die Iteration beschränkt bleibt, und die Iterationsschleife abgebrochen.

Die folgende Funktion führt die beschriebene Iteration durch. x und xt sowie y und yt sind die iterativ benutzten Variablen für die Iterationswerte.

FUNCTION punkt_iteration (cx, cy, max_betrag_quadrat, max_iter)

  betrag_quadrat = 0
  iter = 0
  x = 0
  y = 0

  WHILE ( betrag_quadrat <= max_betrag_quadrat ) AND ( iter < max_iter )
    xt = x * x - y * y + cx
    yt = 2 * x * y + cy
    x = xt
    y = yt
    iter = iter + 1
    betrag_quadrat = x * x + y * y
  WEND

  punkt_iteration = iter

END FUNCTION

Wird ein kontinuierlicherer Farbverlauf gewünscht, so bietet sich alternativ die Formel

    punkt_iteration = iter – log(log(betrag_quadrat) / log(4)) / log(2)

an, die keine ganze sondern eine gebrochene Zahl liefert. Für die Folge mit c=0 und dem Startwert z₀=2 liefert diese Formel den Wert Null. Es ergibt sich ferner eine von max_betrag_quadrat unabhängige Farbgebung, sofern dieser Wert groß gegen 1 ist.

Ein erheblicher Teil der Rechenzeit wird dort benötigt, wo die Zahlenfolge nicht divergiert. Moderne Programme bemühen sich, mit verschiedenen Verfahren die Rechenzeit für diese Stellen zu reduzieren. Eine Möglichkeit besteht darin, die Rechnung bereits abzubrechen, wenn die Zahlenfolge konvergiert ist oder sich in einem periodischen Zyklus gefangen hat. Andere Programme nutzen aus, dass jeder Punkt im Inneren einer geschlossenen Kurve, die nur Punkte aus $\Bbb M$ enthält, ebenfalls dazugehört.

Rezeption in der Öffentlichkeit

Die Mandelbrot-Menge erlangte durch Publikationen von Bildern in den Medien Ende der 1980er Jahre einen für ein mathematisches Thema dieser Art ungewöhnlich großen Bekanntheitsgrad. Sie dürfte das populärste Fraktal und möglicherweise das populärste Objekt der zeitgenössischen Mathematik überhaupt sein.^[2] Ein Aspekt neben dem enormen geometrischen Formenreichtum ist der extreme Kontrast zwischen diesem und der Einfachheit des zugrunde liegenden Algorithmus, der an biologische Systeme erinnert, bei denen nach naturwissenschaftlicher Sicht ebenfalls aus einer vergleichsweise geringen Zahl von Regeln äußerst komplexe Systeme entstehen können. Ein weiterer Aspekt ist die Nähe zur Chaostheorie, die ebenfalls in der Öffentlichkeit großes Interesse geweckt hatte. Die Mandelbrot-Menge hat auch Computerkünstler inspiriert und zu einem Aufschwung fraktaler Konzepte beigetragen. Dabei fanden und finden auch zahlreiche Modifikationen des Algorithmus Anwendung, welcher der Mandelbrot-Menge zugrunde liegt.

Der amerikanische Musiker Jonathan Coulton hat ein Lied über die Mandelbrot-Menge veröffentlicht, in welchem Benoît Mandelbrot dafür gedankt wird, dass er Ordnung in das Chaos gebracht habe.^[3]

Siehe auch

• Fractint (freies Generator-Programm)

Einzelnachweise

1. ↑ Pixel Counting, Mu-Ency at MROB
2. ↑ Peitgen, Jürgens, Saupe: Chaos, Bausteine der Ordnung, Rowohlt, ISBN 3-499-60551-1, Seite 431
3. ↑ http://www.jonathancoulton.com/songdetails/Mandelbrot%20Set

Literatur

• Benoît Mandelbrot: Die fraktale Geometrie der Natur. ISBN 3-7643-2646-8.
• John Briggs und F. David Peat: Die Entdeckung des Chaos. ISBN 3-446-15966-5.
• Heinz-Otto Peitgen und Peter H. Richter: The Beauty of Fractals. ISBN 0-387-15851-0.
• Heinz-Otto Peitgen und Dietmar Saupe: The Science of Fractal Images. ISBN 0-387-96608-0.
• Karl Günter Kröber: Das Märchen vom Apfelmännchen – 1. Wege in die Unendlichkeit. ISBN 3-499-60881-2.
• Karl Günter Kröber: Das Märchen vom Apfelmännchen – 2. Reise durch das malumitische Universum. ISBN 3-499-60882-0.

Weblinks

• Fractalizer Freeware Fraktalprogramm für Microsoft Windows
• The Encyclopedia of the Mandelbrot Set (englisch)
• Fractal Generator (Java-Plugin erforderlich)
• Mandelbrot-Menge als Javaapplet (Java-Plugin (ab Java 5) erforderlich)
• Apfelmännchen als Web-Client/Server Lösung
• Mandelbrot Fractal Explorer Erforschung der Mandelbrot-Menge mit MapClient (OpenLayers)
• Facharbeit über Juliamengen und Mandelbrot-Menge
• Julia- und Mandelbrot-Mengen
• Insbes. Guided Tours und interaktiver Mandelbrot-Explorer
• Schwarz-Weiß-Atlas, etwa 20-fach
• XaoS Fraktal-Generator – unter GPL für viele Betriebssysteme
• Fractal-Explorer – Freeware-Generator für Bilder und Animationen für Microsoft Windows
• Sammlung von Julia- und Mandelbrotfraktalen
• Animationen zur Zoomfahrt im hiesigen Artikel – bis zu 1024×768 Pixeln

±