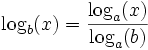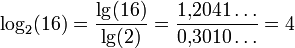Zehnerlogarithmus

Der dekadische Logarithmus, auch Zehnerlogarithmus genannt, ist in der Mathematik der Logarithmus zur Basis 10. Man schreibt verkürzt auch lg(x) oder log(x) statt log₁₀(x). Seine Umkehrfunktion ist 10^x, das heißt: y = 10^x ist gleichbedeutend mit x = lg(y). Einfach ausgedrückt zählt er die Stellen einer Zahl verringert um eins.

log₁₀(1) = 0 weil 10⁰ = 1

log₁₀(10) = 1 weil 10¹ = 10

log₁₀(100) = 2 weil 10² = 100

Er kann aber auch Zwischenwerte abbilden.

log₁₀(5) ≈ 0,69897

log₁₀(50) ≈ 1,69897

log₁₀(75) ≈ 1,87506

In den Zeiten, bevor es Taschenrechner gab, wurden Rechenschieber und bei genaueren Berechnungen dekadische Logarithmen für Multiplikation, Division, Potenz und Wurzel benutzt. Die Logarithmen waren in Logarithmentafeln aufgelistet, die über Jahrhunderte bis in die 1970-er Jahre unentbehrliche Helfer in Schule und Beruf waren.

Die dekadischen Logarithmen werden nach Henry Briggs bisweilen auch Briggsche Logarithmen genannt.

Basisumrechnung

siehe auch: Logarithmus, Basisumrechnung

Heute besitzen viele wissenschaftliche Taschenrechner (beispielsweise in der Schule verwendete Geräte) eine Taste mit der Aufschrift log, die den dekadischen Logarithmus einer Zahl wiedergibt. Möchte man den Logarithmus auf der Basis einer anderen Zahl erhalten und hat aber nur diese eine Taste mit für den Logarithmus auf der Basis 10 zur Verfügung, so kann einem folgende mathematische Gesetzmäßigkeit weiterhelfen:

$\log_{b}(x) = \frac{\log_{a}(x)}{\log_{a}(b)}$

Beispiel

In diesem Rechenbeispiel wird der Logarithmus log₂(16) mit Hilfe des dekadischen Logarithmus errechnet:

$\log_{2}(16) = \frac{\lg(16)}{\lg(2)} = \frac{1{,}2041\dots}{0{,}3010\dots} = 4$

Weblinks

• Eric W. Weisstein: Common Logarithm auf MathWorld (englisch)