Zehnerpotenz

Zehnerpotenzen (vereinzelt, vor allem in der Schulmathematik, auch Stufenzahlen) sind ganzzahlige Potenzen mit der Basis (Grundzahl) 10 und einem beliebigen, ganzzahligen Exponenten (Hochzahl). Ihre Potenzschreibweise lautet dann etwa 10ⁿ mit einer natürlichen Zahl n.

Die Zehnerpotenzen

Alle Zehnerpotenzen haben eigene Zahlennamen:

Name	Zahl in Dezimalschreibweise	Zahl in Exponentialschreibweise
Zehntausendstel	0,0001	10 − 4
Tausendstel	0,001	10 − 3
Hundertstel	0,01	10 − 2
Zehntel	0,1	10 − 1
Eins	1	100
Zehn	10	101
Hundert	100	102
Tausend	1000	103
Zehntausend	10 000	104
Hunderttausend	100 000	105

Verwendung

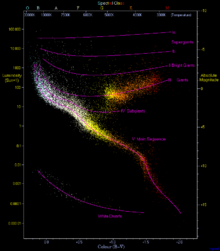Hertzsprung-Russell-Diagramm. Abszisse: Farbindex der Sterne, Ordinate: Leuchtkraft (Sonne = 1) in Zehnerpotenzen

Da unser übliches Zahlensystem, das Dezimalsystem (zu lat. decimus „der Zehnte“), auf Zehnerpotenzen beruht, sind sie geeignet, auch sehr große und sehr kleine Zahlen kompakt zu schreiben. Sie bilden die Grundlage der wissenschaftlichen Schreibweise (kurz SCI für englisch scientific), die die Zahlen auf vorgestellte Mantisse und Exponent der Basis 10 reduzieren kann.

Dazu als Beispiele:

$4711 = 4{,}711 \cdot 10^3$

$4\, 711\, 000 = 4{,}711 \cdot 10^6 = 4{,}711\ \mathrm{Millionen}$

$0{,}000001414 = 1414 \cdot 10^{- 9} = 1{,}414 \cdot 10^{- 6} = 1{,}414\ \mathrm{Millionstel}$

Der Exponent gibt dabei immer die Zahl der Nullen an, wenn dort 10 hoch sechs (10⁶) steht, dann ist es also eine Million.

Auch die Achsen von Diagrammen werden oft nicht linear, sondern in Zehnerpotenzen als logarithmische Skala geteilt, wenn es um sehr große Wertebereiche geht. Ein Beispiel aus der Astronomie – die man ja mit „astronomisch großen Zahlen“ assoziiert – ist das Hertzsprung-Russell-Diagramm, das im nebenstehenden Bild auf der Ordinate eine Skala von 0,00001 bis 100 000 Einheiten der Sonnen-Leuchtkraft L₀ zeigt. Dann liegt aber z. B. in der Mitte zwischen 10 und 100 L₀ nicht der Wert 20 oder 50 – sondern 31,63 L₀. Dieser Wert ist nicht das arithmetische – sondern das quadratische Mittel von 10 und 100, d. h. die Wurzel aus 1000 bzw. 10^1,5.

Rechnen mit Zehnerpotenzen

Es gibt einige einfache Rechenregeln für das Rechnen mit Zehnerpotenzen:

• Multipliziert man eine natürliche Zahl mit einer Stufenzahl, so werden die Nullen der Stufenzahl an die natürliche Zahl angehängt.
• Multipliziert man einen Dezimalbruch mit einer Stufenzahl, so rückt das Komma um so viele Stellen nach rechts, wie die Stufenzahl Nullen hat.
• Dividiert man einen Dezimalbruch durch eine Stufenzahl, so rückt das Komma um so viele Stellen nach links, wie die Stufenzahl Nullen hat.

Zehnerpotenzen und SI-Präfixe

Für Maßeinheiten definiert das Internationale Einheitensystem entsprechende Vorsilben:

SI-Präfixe

Name	Yotta	Zetta	Exa	Peta	Tera	Giga	Mega	Kilo	Hekto	Deka
Symbol	Y	Z	E	P	T	G	M	k	h	da
Faktor	1024	1021	1018	1015	1012	109	106	103	102	101
Name	Yokto	Zepto	Atto	Femto	Piko	Nano	Mikro	Milli	Zenti	Dezi
Symbol	y	z	a	f	p	n	µ	m	c	d
Faktor	10−24	10−21	10−18	10−15	10−12	10−9	10−6	10−3	10−2	10−1

Siehe auch

• Binärzahl zu Zweierpotenzen, als Basis der Datenverarbeitung
• Oktalzahl zu Achterpotenzen
• Hexadezimalzahl zu Sechzehnerpotenzen
• Vigesimalsystem zu Zwanzigerpotenzen
• Hexagesimalsystem zu Sechzigerpotenzen, etwa in der Zeitrechnung
• Lange und kurze Leiter, andere Benennungssysteme für große Zehnerpotenzen