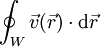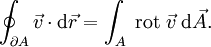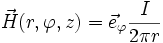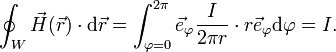Zirkulation (Physik)

In diesem Artikel oder Abschnitt fehlen folgende wichtige Informationen: Es fehlt präzise mathematische Definition, die Beispiele können nachgetragen werden. Du kannst Wikipedia helfen, indem du sie recherchierst und einfügst.

Der mathematische Begriff Zirkulation wird hauptsächlich in der Physik und der Vektoranalysis benutzt. Die Zirkulation eines Vektorfeldes längs eines geschlossenen orientierten Weges ist als das Umlaufintegral des Vektorfeldes über den Weg definiert. Sie ist ein integrales Maß für die Rotationseigenschaft einer Strömung in einem bestimmten Gebiet.

mathematische Formulierung

Ist W ein stückweise glatter, geschlossener und orientierter Weg im 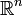$\mathbb{R}^{n}$ (von besonderer Bedeutung ist hier der $\mathbb{R}^3$) und $\vec v$ ein längs dieses Weges integrierbares Vektorfeld, so heißt

$\oint_{W} \vec v(\vec r)\cdot \mathrm{d} \vec r$

Zirkulation von $\vec v$ längs W.

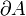Ist ein Vektorfeld $\vec v$ auf einer orientierten und stückweise glatt berandeten Fläche A differenzierbar, so ist nach dem Satz von Stokes die Zirkulation von $\vec v$ längs des zu A gehörigen orientierten Randes $\partial A$ gleich dem Flächenintegral der Rotation von $\vec v$ über A:

$\oint_{\partial A} \vec{v}\cdot\mathrm{d} \vec r = \int_{A} \;\operatorname{rot}\; \vec v \;\mathrm{d} \vec A.$

physikalische Deutung

Zur Veranschaulichung ist folgendes Beispiel aus der Hydrodynamik hilfreich:

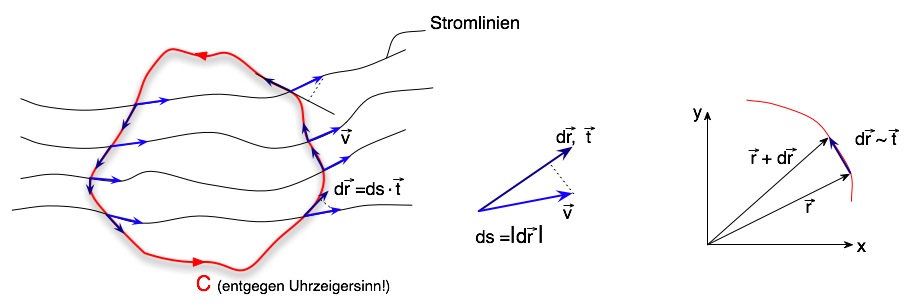
Zu sehen ist eine Kurve C, die von einem Strömungsfeld durchflossen wird. Strömungsfeld und Kurve liegen in derselben Ebene. Die Strömungsgeschwindigkeit ist $\vec v$. Das Wegintegral entlang der Kurve C im obigen Beispiel ist offensichtlich

$\oint\limits_{C}\vec v\ \operatorname{ d}\vec r=\oint\limits_{C}\vec v\cdot \vec t\ \operatorname{d}s$

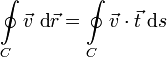
die "Summe" der Tangentialkomponenten von $\vec v$ entlang C. Dabei kann der Wert des Wegintegrals prinzipiell größer, kleiner oder gleich Null sein. D.h. für das obige Beispiel:
$\oint\limits_{C}\vec v\ \operatorname{ d}\vec r=\begin{cases}>0 \text{ ,wenn } \sphericalangle(\vec v,\operatorname{d}\vec r) \text{ ueberwiegend spitz ist, d.h. Bewegung entgegen Uhrzeigersinn } \\ =0 \text{ ,wenn es keine Netto-Drehung der Fluessigkeit gibt}\\ <0 \text{ ,wenn } \sphericalangle(\vec v,\operatorname{d}\vec r) \text{ ueberwiegend stumpf ist, d.h. Bewegung im Uhrzeigersinn }\end{cases}$
Man bezeichnet nun
$\oint\limits_{C}\vec \phi\ \operatorname{ d}\vec r$
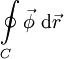
als Zirkulation von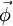 $\vec \phi$ endlang C und hat damit ein Maß für die Umströmung der Kurve C. Je nach Bedeutung des Vektorfeldes 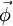$\vec \phi$ findet man andere Begriffe für die Zirkulation wobei es sich um den gleiche mathematische Rahmen handelt.
So bezeichnet man beispielsweise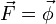 $\vec F=\vec \phi$ als Arbeit und 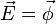$\vec E=\vec \phi$ als Umlaufspannung und meint damit die Zirkulation der Kraft bzw. die Zirkulation der elektrischen Feldstärke. Diese Vektorfelder können also in analoger Weise zu 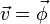$\vec v=\vec \phi$, der Zirkulation im anschaulichen Sinne, behandelt werden.

Beispiele

Zirkulation des Magnetfeldes eines Stromfadens

Ein auf der z-Achse liegender Stromfaden, der in positiver z-Richtung mit dem Strom I durchflossen ist, wird von dem Magnetfeld

$\vec H(r,\varphi,z)= \vec e_\varphi \frac{I}{2\pi r}$

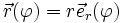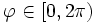umgeben. Die Zirkulation dieses Vektorfeldes entlang eines Kreises $\vec r(\varphi) = r \vec e_r(\varphi)$ mit $\varphi\in[0,2\pi)$ und beliebigem positiven Radius r ist gleich dem Strom I:

$\oint_{W} \vec H(\vec r)\cdot\mathrm{d}\vec r =\int_{\varphi=0}^{2\pi} \vec e_\varphi \frac{I}{2\pi r}\cdot r\vec e_\varphi \mathrm{d}\varphi = I.$

Dieses Beispiel demonstriert, dass für die Anwendbarkeit des Stokes'schen Integralsatzes das betreffende Vektorfeld auf einer von der geschlossenen Kurve berandeten Fläche differenzierbar sein muss. Das Vektorfeld 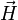$\vec H$ aus diesem Beispiel ist auf der z-Achse nicht definiert. Die Zirkulation wird jedoch entlang eines Kreises gebildet, der die z-Achse umschließt. Der Stokes'sche Integralsatz ist also in diesem Fall nicht anwendbar. Das bestätigt sich dadurch, dass die Zirkulation von 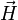$\vec H$ entlang des Kreises den von null verschiedenen Wert I hat, obwohl das Vektorfeld 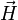$\vec H$ auf seinem gesamten Definitionsgebiet rotationsfrei ist (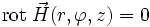$\operatorname{rot}\;\vec H(r,\varphi,z)=0$ für r > 0).

radiale Strömung

starre Rotation

Siehe auch: Zirkulation

Literatur

• Königsberger: Analysis 2. Springer-Verlag Berlin, 1993. ISBN 3-540-54723-1.
• Theodore Frankel: The Geometry of Physics (An Introduction). Cambridge University Press, 1997. ISBN 0-521-38753-1.