- Zorns Lemma
-
Das Lemma von Zorn, auch bekannt als Zorns Lemma, Kuratowski-Zorn-Lemma oder zornsches Lemma, ist ein Theorem der Mengenlehre, genauer gesagt, der Zermelo-Fraenkel-Mengenlehre, die das Auswahlaxiom einbezieht. Es besagt:
- Jede nichtleere halbgeordnete Menge, in der jede Kette (d.h. jede total geordnete Teilmenge) eine obere Schranke hat, enthält mindestens ein maximales Element.
Es ist benannt nach dem deutsch-amerikanischen Mathematiker Max Zorn, der es 1935 entdeckte (unabhängig von der Entdeckung durch Kuratowski 1922).
Die verwendeten Begriffe sind die folgenden: Sei
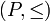 eine halbgeordnete Menge. Eine Teilmenge T von P heißt Kette (oder total geordnet), wenn für alle
eine halbgeordnete Menge. Eine Teilmenge T von P heißt Kette (oder total geordnet), wenn für alle 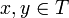 stets
stets 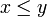 oder
oder 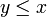 gilt. Eine Teilmenge T von P hat eine obere Schranke
gilt. Eine Teilmenge T von P hat eine obere Schranke 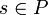 , falls
, falls 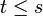 für alle
für alle 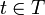 zutrifft. Man beachte, dass s nicht in T liegen muss. Ein maximales Element von P ist ein Element m, für welches es kein größeres Element in P gibt, aus
zutrifft. Man beachte, dass s nicht in T liegen muss. Ein maximales Element von P ist ein Element m, für welches es kein größeres Element in P gibt, aus 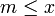 also stets m = x folgt.
also stets m = x folgt.Verwendung
Wie auch der Wohlordnungssatz ist Zorns Lemma äquivalent zum Auswahlaxiom, d.h. man kann mit einem dieser drei Sätze zusammen mit der Zermelo-Fraenkel-Mengenlehre die beiden anderen beweisen. Zorns Lemma wird in vielen wichtigen Beweisen benutzt, zum Beispiel für
- den Satz, dass jeder Vektorraum eine Basis hat,
- das Hahn-Banach-Theorem in der Funktionalanalysis, nach dem man lineare Funktionale fortsetzen kann,
- Tychonoffs Theorem, dass jedes Produkt kompakter Räume in der Produkttopologie selbst kompakt ist,
- den Satz, dass jeder Ring mit 1 ein maximales Ideal hat (bzw. dort sogar jedes Ideal in einem maximalem Ideal liegt),
- den Satz von Ernst Steinitz, dass jeder Körper einen algebraischen Abschluss hat.
Ein Beispiel der Anwendung
Wir beweisen als typische Anwendung des Lemmas von Zorn, dass jeder Ring mit 1 ein maximales Ideal hat. Die Menge P besteht hier aus allen (beidseitigen) Idealen in R, mit Ausnahme von R selbst. Diese Menge ist nichtleer (sie enthält das Nullideal) und bezüglich der Mengeninklusion halbgeordnet. Wenn wir ein maximales Element dieser Menge finden können, dann sind wir fertig, denn das ist ein Ideal ungleich R, für das es kein größeres Ideal in R gibt, also ein maximales Ideal.
Um Zorns Lemma anwenden zu können, nehmen wir eine totalgeordnete Teilmenge T von P und müssen zeigen, dass sie eine obere Schranke hat, also ein Ideal I in R existiert, das alle Ideale in T enthält aber ungleich R ist (sonst wäre es nicht in P). Wir wählen I als die Vereinigung aller Elemente von T. I ist ein Ideal, denn sind a und b Elemente von I, dann gibt es Ideale J,K in T, so dass a in J und b in K liegt. Da T totalgeordnet ist, liegt eins der beiden Ideale im anderen, wir können ohne Einschränkung annehmen, dass J in K enthalten ist. Dann sind a und b beide in K, also liegen a+b und für jedes r in R auch ra und ar in K und damit in I. Somit ist also I tatsächlich ein Ideal von R.
Warum liegt nun I in P, also warum ist I ungleich R? Dazu müssen wir wissen, dass ein Ideal gleich R ist, genau dann wenn es die 1 enthält. (R enthält die 1, und umgekehrt liegt mit der 1 auch jedes Element der Form r1 im Ideal, also ganz R.) Wäre nun also I gleich R, dann müsste es ein Ideal in T geben, das die 1 enthält, und das wäre gleich R, aber R wurde explizit aus P ausgeschlossen.
Da die Voraussetzungen für Zorns Lemma erfüllt sind, erhalten wir die Existenz eines maximalen Elements in P, und das ist ein maximales Ideal von R.
Dieser Beweis benötigt die Voraussetzung, dass der Ring eine 1 hat. Ohne das wäre er nicht durchführbar und tatsächlich wäre die Behauptung falsch.
Beweis von Zorns Lemma mit dem Auswahlaxiom
Zuletzt geben wir noch eine Beweisskizze des Lemmas von Zorn. Angenommen, das Lemma wäre falsch. Dann gäbe es eine halbgeordnete Menge P, in der jede total geordnete Teilmenge eine obere Schranke hätte, aber trotzdem jedes Element ein größeres hätte (es gäbe kein maximales Element in P). Für jede total geordnete Teilmenge T definieren wir nun ein Element b(T), das größer ist als jedes Element in T, indem wir eine obere Schranke von T nehmen und b(T) auf ein Element setzen, das noch größer ist als diese Schranke. Um b hierdurch als Funktion definieren zu können, benötigen wir das Auswahlaxiom (denn wir sagen nicht, welche obere Schranke und welches größere Element wir nehmen).
Mit dieser Funktion b bestimmen wir dann Elemente a0 < a1 < a2 < a3 < ... in P. Diese Folge wird wirklich lang: Die Indizes sind nicht nur alle natürlichen Zahlen, sondern alle Ordinalzahlen. Diese Folge ist zu lang für die Menge P, denn es gibt mehr Ordinalzahlen als Elemente in irgendeiner Menge enthalten sein können, und so erhalten wir einen Widerspruch.
Die av definieren wir durch transfinite Induktion: Wir wählen a0 beliebig aus P (das geht, da P eine obere Schranke der leeren Menge enthält, also selbst nicht leer ist), und für jede andere Ordinalzahl w setzen wir
- aw: = b({av | v < w}).
Das geht, da die av durch diese Konstruktion total geordnet sind.
Wikimedia Foundation.
