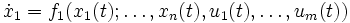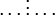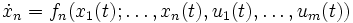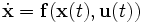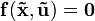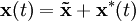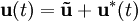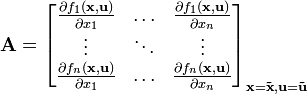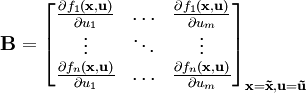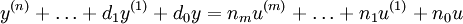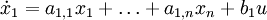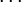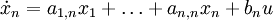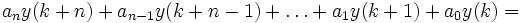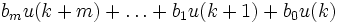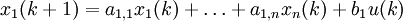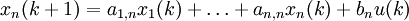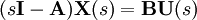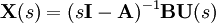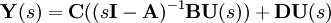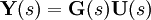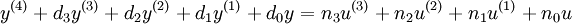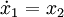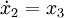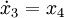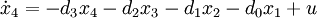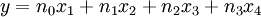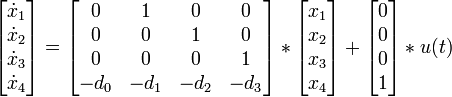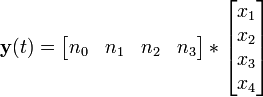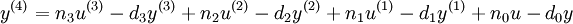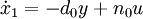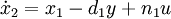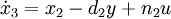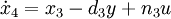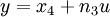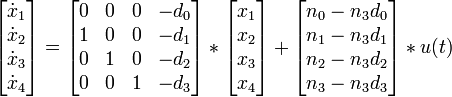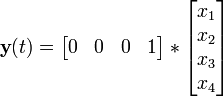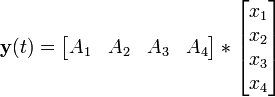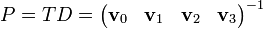Zustandsraumbeschreibung

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Der Zustandsraum bezeichnet die Beschreibung eines dynamischen Systems im Zeitbereich. Hierbei werden die Einzelzustände des Systems zu einem Vektor zusammengefasst, dem Zustandsvektor, der als Ortsvektor eines Punkts im Zustandsraum interpretiert wird. Der Zustandsvektor bewegt sich zeitlich auf einer Kurve, der Trajektorie im Zustandsraum. Für ein gegebenes Eingangssignal geht dabei durch jeden Punkt des Zustandsraums genau eine Trajektorie, was (im zweidimensionalen Fall) graphische Darstellungen ermöglicht. Es handelt sich mathematisch gesehen um einen Phasenraum.

Die Zustandsraumbeschreibung hat gegenüber der Darstellung im Frequenzbereich den Vorteil, dass damit auch nichtlineare und zeitvariante Systeme beschrieben werden können. Auch wird durch die Übertragungsfunktion (ebenso wie durch die Impuls- oder Sprungantwort im Zeitbereich) lediglich das Ein-/Ausgangsverhalten beschrieben, nicht jedoch das, was innerhalb des Systems geschieht.

Nichtlineare Zustandsgleichungen

Ein nichtlineares System n-ter Ordnung kann durch ein System nichtlinearer Differenzialgleichungen 1. Ordnung

$\dot x_1=f_1(x_1(t);\ldots,x_n(t),u_1(t),\ldots,u_m(t))$

$\ldots \vdots \ldots$

$\dot x_n=f_n(x_1(t);\ldots,x_n(t),u_1(t),\ldots,u_m(t))$

oder kompakter als Vektordifferenzialgleichung

$\dot \mathbf{x}=\mathbf{f}(\mathbf{x}(t),\mathbf{u}(t))$

geschrieben werden.

für den Ruhepunkt 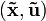$(\mathbf{\tilde x}, \mathbf{\tilde u})$ gilt

$\mathbf{f}(\mathbf{\tilde x},\mathbf{\tilde u})=\mathbf{0}$

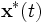Ist $\mathbf{x^*}(t)$ die Abweichung des Systems vom Ruhepunkt, dann gilt

$\mathbf{x}(t)=\mathbf{\tilde x}+\mathbf{x^*}(t)$

$\mathbf{u}(t)=\mathbf{\tilde u}+\mathbf{u^*}(t)$

und

$\mathbf{\dot x}=\mathbf{\dot x^*}$.

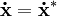Mit der mehrdimensionalen Taylor-Reihe wird das System um den Ruhepunkt linearisiert zu

$\mathbf{\dot x^*}=\mathbf{A}\mathbf{x^*}(t)+\mathbf{B}\mathbf{u^*}(t)$

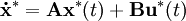
mit den Jacobi-Matrizen

$\mathbf{A}=\begin{bmatrix}\frac{\partial f_1(\mathbf{x},\mathbf{u})}{\partial x_1} & \ldots & \frac{\partial f_1(\mathbf{x},\mathbf{u})}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n(\mathbf{x},\mathbf{u})}{\partial x_1} & \ldots & \frac{\partial f_n(\mathbf{x},\mathbf{u})}{\partial x_n} \end{bmatrix}_{\mathbf{x}=\mathbf{\tilde x},\mathbf{u}=\mathbf{\tilde u}}$

und

$\mathbf{B}=\begin{bmatrix}\frac{\partial f_1(\mathbf{x},\mathbf{u})}{\partial u_1} & \ldots & \frac{\partial f_1(\mathbf{x},\mathbf{u})}{\partial u_m} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n(\mathbf{x},\mathbf{u})}{\partial u_1} & \ldots & \frac{\partial f_n(\mathbf{x},\mathbf{u})}{\partial u_m} \end{bmatrix}_{\mathbf{x}=\mathbf{\tilde x},\mathbf{u}=\mathbf{\tilde u}}$

Beschreibung linearer Systeme

Zeitkontinuierliche lineare Systeme werden durch die lineare Differentialgleichung n-ter Ordnung

$y^{(n)} + \ldots + d_{1}y^{(1)} + d_{0}y = n_{m}u^{(m)} + \ldots + n_{1}u^{(1)} + n_{0}u$

beschrieben. Falls die Koeffizienten d_i und n_k alle konstant sind ist die Laplace-Transformation ausführbar und es gilt die Übertragungsfunktion

$G(s) = \frac{n_{m}s^{m} + \ldots + n_{1}s + n_{0}}{s^{n} + d_{n-1}s^{n-1} + \ldots + d_{1}s + d_{0}}$.

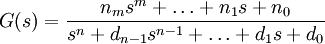Eine Differentialgleichung n-ter Ordnung kann in ein System von n Differentialgleichungen 1. Ordnung

$\dot x_1=a_{1,1}x_1 +\ldots +a_{1,n}x_n + b_1u$

$\ldots$

$\dot x_n=a_{1,n}x_1 +\ldots +a_{n,n}x_n + b_nu$

überführt werden.

Zeitdiskrete lineare Systeme werden durch die lineare Differenzengleichung n-ter Ordnung

$a_ny(k+n)+a_{n-1}y(k+n-1)+\ldots +a_1y(k+1)+a_0y(k)=$

$b_mu(k+m)+\ldots +b_1u(k+1)+b_0u(k)$

beschrieben. Falls die Koeffizienten a_i und b_j alle konstant sind ist die z-Transformation ausführbar und es gilt die Übertragungsfunktion

$G(z)=\frac{b_mz^m+b_{m-1}z^{m-1}+\ldots +b_1z+b_0}{a_nz^n+a_{n-1}z^{n-1}+\ldots +a_1z+a_0}$.

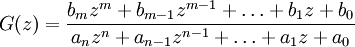Eine Differenzengleichung n-ter Ordnung kann in ein System von n Differenzengleichungen 1. Ordnung

$x_1(k+1)=a_{1,1}x_1(k) +\ldots +a_{1,n}x_n(k) + b_1u(k)$

$\ldots$

$x_n(k+1)=a_{1,n}x_1(k) +\ldots +a_{n,n}x_n(k) + b_nu(k)$

überführt werden.

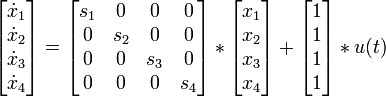
Lineare Zustandsgleichungen

Signalflussplan Zustandsraum

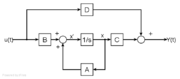
Für zeitkontinuierliche Systeme lauten die linearen Grundgleichungen in vektorieller Form:

$\dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u}$
$\mathbf{y}=\mathbf{C}\mathbf{x}+\mathbf{D}\mathbf{u}$

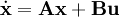
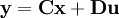
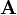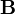Der Zustand x ist der Zustandsvektor. Über die Matrizen $\mathbf{A}$ und $\mathbf{B}$ sind die Verkettungen der einzelnen Zustände, samt die Zugriffe über die Steuervariablen (Eingangsgrößen) 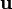$\mathbf{u}$ darstellbar. Die Matrix 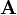$\mathbf{A}$ wird als Systemmatrix, 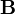$\mathbf{B}$ als Steuermatrix bezeichnet. Mittels der Koppel- oder Beobachtungsmatrix 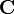$\mathbf{C}$ sind die Verkettungen der Ausgangsgrößen 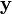$\mathbf{y}$ beschreibbar. Die Durchgangsmatrix 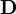$\mathbf{D}$ beschreibt die Durchgriffe des Systems, sie ist bei nicht sprungfähigen Systemen Null.

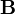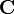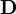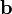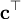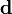Einen wichtigen Sonderfall stellen Systeme mit einer Ein- und einer Ausgangsgröße dar (SISO Single Input, Single-Output Systeme). Hier sind $\mathbf{B}$ und $\mathbf{C}$ Vektoren und $\mathbf{D}$ ein Skalar. Es werden dann häufig die Formelzeichen $\mathbf{b}$, $\mathbf{c}^\top$ und $\mathbf{d}$ verwendet.

In vielen Fällen interessiert anstelle eines kontinuierlichen Verlaufs nur der Systemzustand zu diskreten Zeitpunkten, beispielsweise den Abtastzeitpunkten bei Regelung durch einen Digitalrechner. In diesem Fall ist 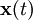$\mathbf{x}(t)$ anstelle einer vektorwertigen Funktion der Zeit eine Folge 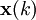$\mathbf{x}(k)$ von Vektoren. An die Stelle der Zustandsdifferentialgleichung tritt dann eine Differenzengleichung.

Die Typen der linearen Grundgleichungen:

System-Typ	Zustandsraum-Modell
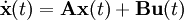
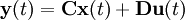
Kontinuierlich Zeitinvariant	$\dot{\mathbf{x}}(t) = \mathbf{A} \mathbf{x}(t) + \mathbf{B} \mathbf{u}(t)$ $\mathbf{y}(t) = \mathbf{C} \mathbf{x}(t) + \mathbf{D} \mathbf{u}(t)$
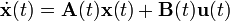
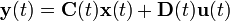
Kontinuierlich Zeitvariant	$\dot{\mathbf{x}}(t) = \mathbf{A}(t) \mathbf{x}(t) + \mathbf{B}(t) \mathbf{u}(t)$ $\mathbf{y}(t) = \mathbf{C}(t) \mathbf{x}(t) + \mathbf{D}(t) \mathbf{u}(t)$
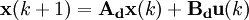
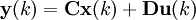
Diskret Zeitinvariant	$\mathbf{x}(k+1) = \mathbf{A_d} \mathbf{x}(k) + \mathbf{B_d} \mathbf{u}(k)$ $\mathbf{y}(k) = \mathbf{C} \mathbf{x}(k) + \mathbf{D} \mathbf{u}(k)$
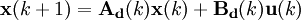
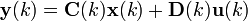
Diskret Zeitvariant	$\mathbf{x}(k+1) = \mathbf{A_d}(k) \mathbf{x}(k) + \mathbf{B_d}(k) \mathbf{u}(k)$ $\mathbf{y}(k) = \mathbf{C}(k) \mathbf{x}(k) + \mathbf{D}(k) \mathbf{u}(k)$
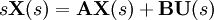
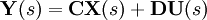
Laplace-Transformierte Kontinuierlich Zeitinvariant	$s \mathbf{X}(s) = \mathbf{A} \mathbf{X}(s) + \mathbf{B} \mathbf{U}(s)$ $\mathbf{Y}(s) = \mathbf{C} \mathbf{X}(s) + \mathbf{D} \mathbf{U}(s)$
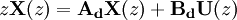
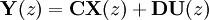
Z-Transformierte Diskret Zeitinvariant	$z \mathbf{X}(z) = \mathbf{A_d} \mathbf{X}(z) + \mathbf{B_d} \mathbf{U}(z)$ $\mathbf{Y} (z) = \mathbf{C} \mathbf{X}(z) + \mathbf{D} \mathbf{U}(z)$

Für die letzten beiden Fälle wurde davon ausgegangen, dass der Anfangszustand des Systems 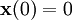$\mathbf{x}(0) = 0$ ist (siehe Differentiationssatz der Laplace-Transformation bzw. Differenzensatz der Z-Transformation).

Die zeitdiskrete Zustandsdarstellung wird aus der kontinuierlichen Form mittels Diskretisierung über einer festen Zeitschrittweite T in der Form

$\mathbf{A_d}=e^{\mathbf{A}T}$

$\mathbf{B_d}=\int_0^Te^{\mathbf{A}\tau}\mathbf{B}d\tau$

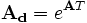
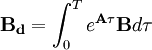
gewonnen. Gilt 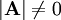$\vert\mathbf{A}\vert \ne 0$ ergibt das Integral

$\mathbf{B_d}=\mathbf{A}^{-1}(e^{\mathbf{A}T}-\mathbf{I})\mathbf{B}$.

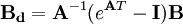Die diskrete Form ist besonders für Berechnungen in Echtzeit geeignet. In Echtzeit wird zuerst die Ausgangsgleichung gerechnet, und danach erst die Zustandsdifferenzengleichung zur Ermittlung der Zustände für den nächsten Berechnungsschritt. Die zeitkontinuierliche Darstellung eignet sich hingegen gut für Simulationen ohne Echtzeit-Ansprüche, durch numerische Integration. Die Exaktheit kann hier durch die Wahl des Integrationsverfahrens und die Anpassung der statischen oder dynamischen Schrittweite beeinflusst werden.

Von zentraler Bedeutung ist die Systemmatrix, aus der die Eigenwerte, und damit die Systemdynamik und deren Stabilität abgeleitet werden kann (charakteristisches Polynom). Ist die Durchgriffsmatrix keine Nullmatrix, haben die Systemeingänge zeitgleichen Einfluss auf die Ausgänge, was zu einer algebraischen Schleife führen kann.

Sind A, B, C, D konstant, so ist das System linear und zeitinvariant, d. h. ein sog. LZI-System.

Ähnlichkeitstransformation

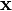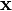Die Zustandsraumdarstellung ist nicht eindeutig. Zum gleichen System existieren unendlich viele Zustandsraumdarstellungen. Anstatt der gewohnten Zustandsvariablen $\mathbf{x}$ kann man auch einen neuen Satz an Zustandsvariablen $\mathbf{z}$ benutzen, falls man $\mathbf{z}$ durch $\mathbf{x}$ beschreiben kann. 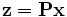$\mathbf{z} = \mathbf{P} \mathbf{x}$, wobei 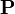$\mathbf{P}$ eine reguläre, lineare Transformationsmatrix ist, d. h. 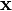$\mathbf{z}$ muss durch $\mathbf{x}$ ohne Hinzufügen von Eingängen oder Ableitungen beschreibbar sein.

Es gilt dann: $\{\mathbf{A},\mathbf{B},\mathbf{C},\mathbf{D}\} \to \{\mathbf{PAP}^{-1},\mathbf{PB},\mathbf{CP}^{-1},\mathbf{D}\}$

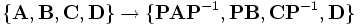
Die neue Zustandsraumdarstellung beschreibt das gleiche System. Es ist deshalb selbstverständlich, dass alle Systemeigenschaften bei der Transformation unverändert bleiben.

Übertragungsfunktion

Die „Übertragungsfunktion“ eines kontinuierlichen zeitinvarianten Zustandsraum-Modells kann auf folgende Weise hergeleitet werden:

$\dot{\mathbf{x}}(t) = \mathbf{A} \mathbf{x}(t) + \mathbf{B} \mathbf{u}(t)$

durch die Laplace-Transformation erhält man

$s\mathbf{X}(s) = \mathbf{A} \mathbf{X}(s) + \mathbf{B} \mathbf{U}(s)$

$(s\mathbf{I} - \mathbf{A})\mathbf{X}(s) = \mathbf{B}\mathbf{U}(s)$

$\mathbf{X}(s) = (s\mathbf{I} - \mathbf{A})^{-1}\mathbf{B}\mathbf{U}(s)$

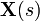womit $\mathbf{X}(s)$ in der Ausgangs-Gleichung substituiert wird

$\mathbf{Y}(s) = \mathbf{C}\mathbf{X}(s) + \mathbf{D}\mathbf{U}(s)$

$\mathbf{Y}(s) = \mathbf{C}((s\mathbf{I} - \mathbf{A})^{-1}\mathbf{B}\mathbf{U}(s)) + \mathbf{D}\mathbf{U}(s)$

und die Übertragungsfunkion ergibt

$\mathbf{Y}(s) = \mathbf{G}(s)\mathbf{U}(s)$

$\mathbf{G}(s) = \mathbf{C}(s\mathbf{I} - \mathbf{A})^{-1}\mathbf{B} + \mathbf{D}$

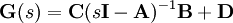
Hierbei entspricht 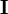$\mathbf{I}$ der Einheitsmatrix $\mathbf{E}$ .

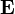Allgemeine Lösung im Zeitbereich

Die allgemeine Lösung im Zeitbereich erhält man durch:

$\mathbf{x}(t) = e^{\mathbf{A}t} \mathbf{x_0} + \int_0^t {e^{\mathbf{A}(t - \tau )} \mathbf{Bu}(\tau )} d\tau$

$\mathbf{y}(t) = \mathbf{C}e^{\mathbf{A}t} \mathbf{x_0} + \mathbf{C}\int_0^t {e^{\mathbf{A}(t - \tau )} \mathbf{Bu}(\tau )} d\tau + \mathbf{Du}(t)$

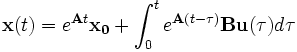
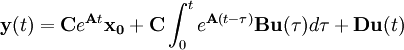
Schwierigkeiten kann dabei die Matrixexponentialfunktion bereiten, die analog zur skalaren Exponentialfunktion definiert ist durch die Potenzreihe

$e^{\mathbf{A}t} = I + \mathbf{A}t + \frac{1}{2!} (\mathbf{A}t)^2 + \frac{1}{3!} (\mathbf{A}t)^3 + \cdots$

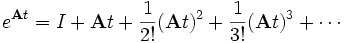
Um hier einen geschlossenen Ausdruck angeben zu können, ist es hilfreich, 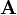$\mathbf{A}$ mittels Hauptachsentransformation auf Diagonalgestalt zu transformieren. Für eine Diagonalmatrix der Form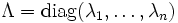

$\Lambda = \operatorname{diag}(\lambda_1,\ldots,\lambda_n)$

ergibt sich dann die Matrixexponentialfunktion zu

$e^{\Lambda t} = \operatorname{diag}(e^{\lambda_1 t},\ldots,e^{\lambda_n t})$

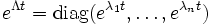
Normalformen

Normalformen werden benutzt, um strukturelle Eigenschaften eines Systems klar hervor zu heben. Oft besitzt ein System in der Zustandsraumdarstellung Zustandsvariablen, welche sich im Übertragungsverhalten des Systems nicht bemerkbar machen. So kann es z. B. sein, dass sich Pole und Nullstellen kürzen, sodass diese keinerlei Einfluss auf die Übertragungsfunktion G(s) haben. Diesen Fall nennt man eine Nichtminimal-Realisierung des Systems, und dies führt dazu, dass das System entweder nicht steuerbar, nicht beobachtbar, oder weder steuerbar noch beobachtbar ist.

Regelungsnormalform

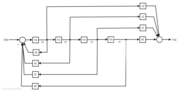
Signalflussplan Regelungsnormalform

Die gegebene Übertragungsfunktion kann mit folgendem Ansatz in eine Zustandsraumdarstellung überführt werden.

Die gegebene Übertragungsfunktion wird in die Zähler- und Nennerfaktoren ausmultipliziert

$\textbf{G}(s) = \frac{n_{3}s^{3} + n_{2}s^{2} + n_{1}s + n_{0}}{s^{4} + d_{3}s^{3} + d_{2}s^{2} + d_{1}s + d_{0}}$.

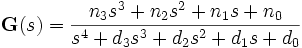Zu dieser Übertragungsfunktion im Frequenzbereich gehört im Zeitbereich die Differentialgleichung (DGL):

$y^{(4)} + d_{3}y^{(3)} + d_{2}y^{(2)} + d_{1}y^{(1)} + d_{0}y = n_{3}u^{(3)} + n_{2}u^{(2)} + n_{1}u^{(1)} + n_{0}u \,$

Aus dieser DGL ergeben sich für die ZR - Darstellung nach Regelungsnormalform folgende Zustandsgleichungen:

$\dot{x}_{1} = x_{2}$

$\dot{x}_{2} = x_{3}$

$\dot{x}_{3} = x_{4}$

$\dot{x}_{4} = -d_{3}x_{4} -d_{2}x_{3} -d_{1}x_{2} -d_{0}x_{1} + u$

$y = n_{0}x_{1} + n_{1}x_{2} + n_{2}x_{3} + n_{3}x_{4}\,$

Die Koeffizienten können nun einfach direkt in die Zustandsmatrizen eingetragen werden:

$\begin{bmatrix} \dot{x}_{1}\\ \dot{x}_{2}\\ \dot{x}_{3}\\ \dot{x}_{4}\\ \end{bmatrix} = \begin{bmatrix} 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ -d_{0}& -d_{1}& -d_{2}& -d_{3} \end{bmatrix} * \begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ 0\\ 1\\ \end{bmatrix} * u(t)$

$\mathbf{y}(t) = \begin{bmatrix} n_{0}& n_{1}& n_{2}& n_{3} \end{bmatrix} * \begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ \end{bmatrix}$

Die Transformationsmatrix folgt aus der Steuerbarkeitsmatrix

$Q_s=\begin{pmatrix} B & A \cdot B & A^2 \cdot B & A^3 \cdot B \end{pmatrix}$.

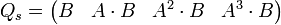Wenn 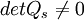$det Q_s \not = 0$ ist das System steuerbar. Dann kann aus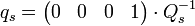

$q_s=\begin{pmatrix} 0 & 0 & 0 & 1\end{pmatrix}\cdot Q_s^{-1}$

die Transformationsmatrix

$P=T_R=\begin{pmatrix} q_s & q_s \cdot A & q_s \cdot A^2 & q_s \cdot A^3 \end{pmatrix}^T$

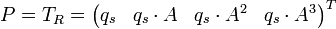
gebildet werden.

Beobachtungsnormalform

Signalflussplan Beobachtungsnormalform

Die Differenzialgleichung nach 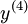$y^{(4)}\,$ aufgelöst

$y^{(4)} = n_{3}u^{(3)} - d_{3}y^{(3)} + n_{2}u^{(2)} - d_{2}y^{(2)} + n_{1}u^{(1)} - d_{1}y^{(1)} + n_{0}u - d_{0}y \,$

und 4 mal integriert ergibt

$y = \int (n_{3}u - d_{3}y)dt +\int \int (n_{2}u -d_{2}y)dt^2 + \int \int \int (n_{1}u - d_{1}y)dt^3 + \int \int \int \int (n_{0}u - d_{0}y)dt^4$.

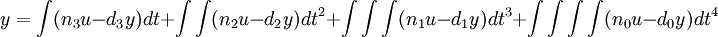Daraus lassen sich die Zustandsgrössen

$\dot{x}_{1} = -d_0y+n_0u$

$\dot{x}_{2} = x_1 -d_1y+n_1u$

$\dot{x}_{3} = x_2 -d_2y+n_2u$

$\dot{x}_{4} = x_3 -d_3y+n_3u$

und die Ausgangsgleichung

$y = x_4 + n_3u \,$

ableiten. Einsetzen von y ergibt

$\dot{x}_{1} = -d_0x_4 + (n_0-n_3d_0)u$

$\dot{x}_{2} = -d_1x_4 + x_1 + (n_1-n_3d_1)u$

$\dot{x}_{3} = -d_2x_4 + x_2 +(n_2-n_3d_2)u$

$\dot{x}_{4} = -d_3x_4 + x_3 +(n_3-n_3d_3)u$.

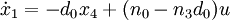
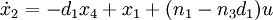
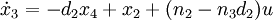
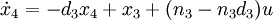oder in Matrix-Form

$\begin{bmatrix} \dot{x}_{1}\\ \dot{x}_{2}\\ \dot{x}_{3}\\ \dot{x}_{4}\\ \end{bmatrix} = \begin{bmatrix} 0& 0& 0& -d_0\\ 1& 0& 0& -d_1\\ 0& 1& 0& -d_2\\ 0& 0& 1& -d_3 \end{bmatrix} * \begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ \end{bmatrix} + \begin{bmatrix} n_0-n_3d_0\\ n_1-n_3d_1\\ n_2-n_3d_2\\ n_3-n_3d_3\\ \end{bmatrix} * u(t)$

$\textbf{y}(t) = \begin{bmatrix} 0& 0& 0& 1 \end{bmatrix} * \begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ \end{bmatrix}$

Die Transformationsmatrix folgt aus der Beobachtbarkeitsmatrix

$Q_b=\begin{pmatrix}C&C\cdot A&C \cdot A^2&C \cdot A^3 \end{pmatrix}^T$

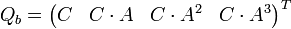
Wenn 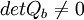$det Q_b \not = 0$ ist das System beobachtbar. Dann kann aus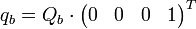

$q_b=Q_b \cdot \begin{pmatrix}0 &0 &0 & 1\end{pmatrix}^T$

die Transformationsmatrix

$P=T_B=\begin{pmatrix}q_b & A \cdot q_b & A^2 \cdot q_b & A^3 \cdot q_b \end{pmatrix}^{-1}$

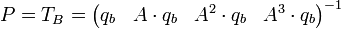
gebildet werden.

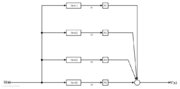
Kanonische Normalform

Signalflussplan Diagonalform

Hat die Übertragungsfunktion G(s) einfache, reelle Polstellen s_kkann eine Partialbruchzerlegung der Form

$G(s)=\sum_{k=1}^4\frac {A_k}{s-s_k}$

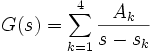
durchgeführt werden. Aus

$Y_k(s)=\frac {1}{s-s_k}U(s)$

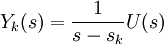
ergeben sich durch Rücktransformation die Zustandsgleichungen

$\dot x_k=s_kx_k+u$

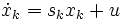
und die Ausgangsgrösse

$y=\sum_{k=1}^4A_kx_k$.

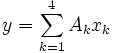In Matrizenschreibweise

$\begin{bmatrix} \dot{x}_{1}\\ \dot{x}_{2}\\ \dot{x}_{3}\\ \dot{x}_{4}\\ \end{bmatrix} = \begin{bmatrix} s_1& 0& 0& 0\\ 0& s_2& 0& 0\\ 0& 0& s_3& 0\\ 0& 0& 0& s_4 \end{bmatrix} * \begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ \end{bmatrix} + \begin{bmatrix} 1\\ 1\\ 1\\ 1\\ \end{bmatrix} * u(t)$

und

$\textbf{y}(t) = \begin{bmatrix} A_1& A_2& A_3& A_4 \end{bmatrix} * \begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ \end{bmatrix}$

Die Zustandsgleichungen sind in diesem Fall entkoppelt. Die Transformationsmatrix wird aus den zu den Eigenwerten s_kder Systemmatrix gehörenden Eigenvektoren 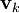$\textbf{v}_k$ in der Form

$P=TD=\begin{pmatrix}\textbf{v}_0 & \textbf{v}_1 & \textbf{v}_2 & \textbf{v}_3 \end{pmatrix}^{-1}$

geschrieben.

Literatur

• Heinz Unbehauen: Regelungstechnik II, Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, 1997, ISBN 3-528-63348-4