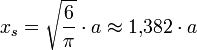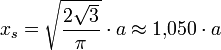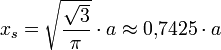Äquivalenzdurchmesser

Der Äquivalentdurchmesser (v. lat.: aequus = gleich + valere = wert sein) ist ein Maß für die Größe eines unregelmäßig geformten Partikels wie beispielsweise eines Sandkorns. Er berechnet sich aus dem Vergleich einer Eigenschaft des unregelmäßigen Teilchens mit einer Eigenschaft eines regelmäßig geformten Teilchens. Je nach Auswahl der zum Vergleich herangezogenen Eigenschaft unterscheidet man verschiedene Äquivalentdurchmesser. Dieser ist eine wichtige Größe in der mechanischen Verfahrenstechnik.

Soll zusätzlich zur Größe eines Teilchens auch noch Informationen über die Teilchenform berücksichtigt werden, so kann man anhand mehrerer Äquivalentdurchmesser sogenannte Formfaktoren definieren.

Geometrische Äquivalentdurchmesser

Einen geometrischen Äquivalentdurchmesser erhält man durch Bestimmung des Durchmessers einer Kugel mit gleicher geometrischer Eigenschaft (Oberfläche oder Volumen) wie das unregelmäßig geformte Partikel.

Volumenäquivalenter Kugeldurchmesser

Der volumenäquivalente Kugeldurchmesser (Formelzeichen x_v) gibt den Durchmesser einer Kugel mit gleichem Volumen an wie das betrachtete Teilchen. Für einfache geometrische Körper kann x_v leicht berechnet werden:

• Würfel: Das Volumen eines Würfels mit Kantenlänge a ist V = a³. Durch Gleichsetzen mit dem Volumen 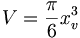$V=\frac{\pi}{6}x_v^3$ einer volumengleichen Kugel mit Durchmesser x_v erhält man für den Äquivalentdurchmesser

$x_v=\sqrt[3]{\frac{6}{\pi}}\cdot a\approx 1{,}241\cdot a$

• Oktaeder: Ein Oktaeder mit Kantenlänge a besitzt das Volumen 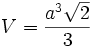$V=\frac{a^3\sqrt{2}}{3}$, daraus ergibt sich ein Äquivalentdurchmesser von

$x_v=\sqrt[3]{\frac{2\sqrt2}{\pi}}\cdot a\approx 0{,}9656\cdot a$

• Tetraeder: Für das Tetraeder mit 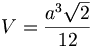$V=\frac{a^3\sqrt2}{12}$ ergibt sich analog

$x_v=\sqrt[3]{\frac{\sqrt2}{2\pi}}\cdot a\approx 0{,}6083\cdot a$

Oberflächenäquivalenter Kugeldurchmesser

Analog zum volumenäquivalenten Kugeldurchmesser ist der oberflächenäquivalente Kugeldurchmesser (Formelzeichen x_s) als der Durchmesser einer Kugel definiert, die dieselbe Oberfläche besitzt wie das untersuchte Teilchen. Auch hier lässt sich unter Zuhilfenahme der Formel für die Kugeloberfläche 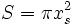$S=\pi x_s^2$ für einfache geometrische Körper ein Äquivalentdurchmesser berechnen:

• Würfel: Mit S = 6a² erhält man

$x_s=\sqrt{\frac{6}{\pi}}\cdot a\approx 1{,}382\cdot a$

• Oktaeder: Über die Oberfläche 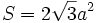$S=2\sqrt3a^2$ ergibt sich

$x_s=\sqrt{\frac{2\sqrt3}{\pi}}\cdot a\approx 1{,}050\cdot a$

• Tetraeder: Die Oberfläche des Tetraeders ist 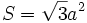$S=\sqrt3a^2$, damit wird

$x_s=\sqrt{\frac{\sqrt3}{\pi}}\cdot a\approx 0{,}7425\cdot a$

Physikalische Äquivalentdurchmesser

Vergleicht man physikalische Eigenschaften des Teilchens wie bspw. die Sinkgeschwindigkeit in einer Flüssigkeit, den Widerstand in einem elektrischen Feld oder die Streulichtintensität, so spricht man von physikalischen Äquivalentdurchmessern.

Aerodynamischer Durchmesser

Der aerodynamische Durchmesser eines Partikels entspricht dem Durchmesser einer Kugel mit der Dichte 1 g/cm³, welche die gleiche Sinkgeschwindigkeit in Luft wie das Partikel hat.