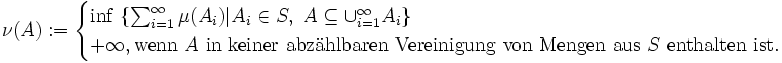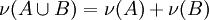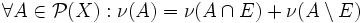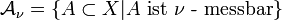- Äusseres Mass
-
Äußeres Maß ist ein Begriff aus dem mathematischen Teilgebiet der Maßtheorie, der 1914 von Constantin Carathéodory eingeführt wurde. Ein äußeres Maß ν ist eine Mengenfunktion von der Potenzmenge einer Menge X in das Intervall
![[0, \infty]](/pictures/dewiki/51/315e0047ccbfa87354192dac2fe986fb.png) , welche folgende Axiome erfüllt:
, welche folgende Axiome erfüllt:Die letzte Eigenschaft wird als σ-Subadditivität bezeichnet.
Der Name äußeres Maß lehnt sich an die Begriffe inneres und äußeres Maß an, die von Borel und Lebesgue benutzt wurden. Die Theorie von Carathéodory benutzt kein inneres Maß und vereinfacht die grundlegenden Beweise beträchtlich.
Inhaltsverzeichnis
Konstruktion des Äußeren Maßes
Sei
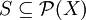 beliebiges Mengensystem mit
beliebiges Mengensystem mit 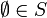 und
und ![\mu: S\rightarrow [0,+\infty]](/pictures/dewiki/100/d5cb9df52542e6e1fd5a3d3dd1a01dbe.png) eine Abbildung mit
eine Abbildung mit 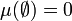 . Gilt für alle
. Gilt für alle 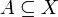 :
:dann ist ν ein äußeres Maß auf
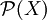 .
.Metrisches äußeres Maß
Ein metrisches äußeres Maß, ist ein äußeres Maß mit der zusätzlichen Eigenschaft:
für separierte Mengen A und B.
Beispiel
- Zur Konstruktion des Lebesgue-Maßes λ wird ein metrisches äußeres Maß λ * verwendet.
Messbarkeit nach Carathéodory
Sei
![\nu:\mathcal{P}(X)\to [0,\infty]](/pictures/dewiki/54/6aae4e28e9c459025c3f4bab648ed2bf.png) ein äußeres Maß auf der Potenzmenge einer Menge X. Eine Menge
ein äußeres Maß auf der Potenzmenge einer Menge X. Eine Menge 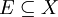 heißt messbar bezüglich ν, falls
heißt messbar bezüglich ν, fallsDabei ist zu beachten, dass der Begriff Messbarkeit in der Maßtheorie zwei Bedeutungen hat, nämlich zum einen Messbarkeit bezüglich eines Messraums und zum anderen die Messbarkeit nach Carathéodory bezüglich eines äußeren Maßes.
Dieser Begriff der Messbarkeit stammt von Constantin Carathéodory.
Beispiele
- Sei
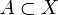 Menge mit:
Menge mit:
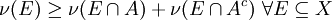
- Dann ist A ν-messbar. Denn aus der σ-Subadditivität des äußeren Maßes folgt:
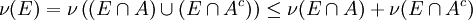
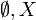 sind ν-messbar.
sind ν-messbar.- Nullmengen sind messbar: Sei
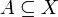 mit ν(A) = 0. Dann ist A ν-messbar.
mit ν(A) = 0. Dann ist A ν-messbar.
σ-Algebra der ν messbaren Mengen
Ist ν ein äußeres Maß, so ist die Menge
eine σ-Algebra und
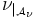 ein vollständiges Maß.
ein vollständiges Maß.Siehe auch
Literatur
- Jürgen Elstrodt: Maß- und Integrationstheorie. 4. Auflage, Springer, Berlin 2005, ISBN 3-540-21390-2, Kapitel II § 4.1.
- Heinz Bauer: Maß- und Integrationstheorie. 2. Auflage, De Gruyter, Berlin 1992, ISBN 3-11-013626-0 (Gebunden), ISBN 3-11-013625-2 (Broschiert), § 5.
Wikimedia Foundation.

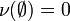
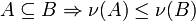 „
„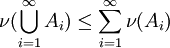 „
„