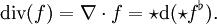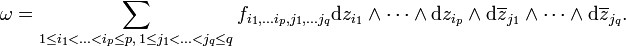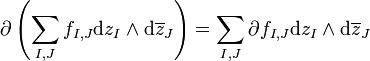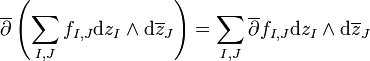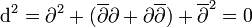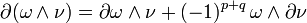- Äußere Ableitung
-
Die äußere Ableitung oder Cartan-Ableitung ist eine Funktion aus den Bereichen Differentialgeometrie und Analysis. Die äußere Ableitung verallgemeinert das aus der Analysis bekannte Leibniz'sche Differential auf den Raum der Differentialformen. Man darf diesen Operator jedoch nicht mit der äußeren Ableitung, welche im Zusammenhang mit der Kettenregel steht, verwechseln. Der Name Cartan-Ableitung erklärt sich daher, dass Élie Cartan der Begründer der Theorie der Differentialformen ist.
Inhaltsverzeichnis
Äußere Ableitung
Definition
Sei M eine n-dimensionale Mannigfaltigkeit und U eine offene Teilmenge. Mit
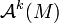 wird hier der Raum der k-Formen auf der Mannigfaltigkeit M bezeichnet. So gibt es dann für alle
wird hier der Raum der k-Formen auf der Mannigfaltigkeit M bezeichnet. So gibt es dann für alle 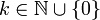 genau eine Funktion
genau eine Funktion 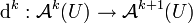 , so dass die folgenden Eigenschaften gelten:
, so dass die folgenden Eigenschaften gelten:- d ist eine Antiderivation, das heißt für
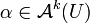 und
und 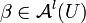 gilt
gilt  .
. - Sei
 , dann ist df definiert als das totale Differential.
, dann ist df definiert als das totale Differential. 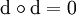
- Der Operator verhält sich natürlich in Bezug auf Einschränkungen, das heißt: Sind
 offene Mengen und
offene Mengen und 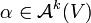 , so gilt d(α | U) = (dα) | U.
, so gilt d(α | U) = (dα) | U.
Es muss natürlich bewiesen werden, dass ein solcher Operator existiert und eindeutig ist. Dieser trägt den Namen äußere Ableitung oder Cartan-Ableitung und wird meistens mit d bezeichnet. Man verzichtet also auf den Index, welcher den Grad der Differentialform angibt, auf welchen der Operator angewendet wird.
Formel für die äußere Ableitung
Man kann die äußere Ableitung auch mit Hilfe der Formel
darstellen, dabei bedeutet das Zirkumflex ^ in
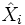 , dass das entsprechende Argument wegzulassen ist, [.,.] bezeichnet die Lie-Klammer.
, dass das entsprechende Argument wegzulassen ist, [.,.] bezeichnet die Lie-Klammer.Koordinatendarstellung
Sei
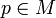 ein Punkt auf einer glatten Mannigfaltigkeit. Die äußere Ableitung von
ein Punkt auf einer glatten Mannigfaltigkeit. Die äußere Ableitung von 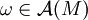 hat in diesem Punkt die Darstellung
hat in diesem Punkt die Darstellung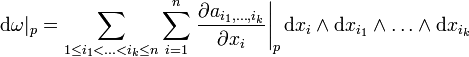 ,
,
dabei hat ω die lokale Darstellung
 .
.Pullback
Seien
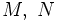 zwei glatte Mannigfaltigkeiten und
zwei glatte Mannigfaltigkeiten und 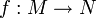 eine einmal stetig differenzierbare Funktion. Dann ist der Pullback
eine einmal stetig differenzierbare Funktion. Dann ist der Pullback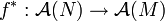 ein Homomorphismus, so dass
ein Homomorphismus, so dass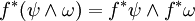 und
und- f * (dω) = d(f * ω)
gilt.
Adjungierte äußere Ableitung
Mit
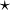 wird im Folgenden der Hodge-Stern-Operator bezeichnet. Der Operator
wird im Folgenden der Hodge-Stern-Operator bezeichnet. Der Operator  ist definiert durch
ist definiert durch 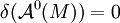 und auf
und auf 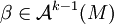 durch
durchDieser Operator ist linear und es gilt
 . Außerdem ist δ der zu d adjungierte Operator. Sei g eine Riemannsche Metrik und
. Außerdem ist δ der zu d adjungierte Operator. Sei g eine Riemannsche Metrik und 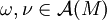 so gilt
so gilt- g(dω,ν) = g(ω,δν).
Verallgemeinerung weiterer Differentialoperatoren
Die aus der Vektoranalysis bekannten Differentialoperatoren kann man mit Hilfe der äußeren Ableitung und dem Hodge-Stern-Operator auf Mannigfaltigkeiten erweitern. Insbesondere erhält man für die Rotation eine Formel, welche auf n-dimensionalen Räumen operiert. Im Folgenden sei M immer eine glatte Riemannsche Mannigfaltigkeit.
Flat- und Sharp-Isomorphismus
Diese beiden Isomorphismen werden durch die Riemannsche Metrik induziert. Sie bilden Tangentialvektoren auf Kotangentialvektoren ab und umgekehrt. Zum Verständnis reicht es an dieser Stelle die Wirkung der Isomorphismen im 3-dimensionallen Raum zu demonstrieren. Sei
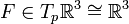 ein Vektorfeld, so gilt für den Flat-Operator in Standardkoordinaten von F
ein Vektorfeld, so gilt für den Flat-Operator in Standardkoordinaten von F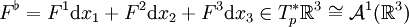 .
.
Der Flat-Operator bildet also Vektorfelder in ihren Dualraum ab. Der Sharp-Operator ist die dazu inverse Operation. Sei
 ein Kovektorfeld (bzw. eine 1-Form), so gilt (ebenfalls Standardkoordinaten)
ein Kovektorfeld (bzw. eine 1-Form), so gilt (ebenfalls Standardkoordinaten) .
.
Kreuzprodukt
Das Kreuzprodukt ist zwar kein Differentialoperator, jedoch wird es in der Vektoranalysis nur für 3-dimensionale Vektorräume definiert. Außerdem ist das Kreuzprodukt wichtig für die Definition der Rotation. Sei V ein Vektorraum und
 zwei Elemente einer äußeren Potenz von V, dann ist das verallgemeinerte Kreuzprodukt definiert durch
zwei Elemente einer äußeren Potenz von V, dann ist das verallgemeinerte Kreuzprodukt definiert durch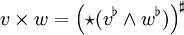 .
.
Für eine Begründung dieser Definition siehe unter äußere Algebra.
Gradient
Es sei
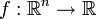 eine differenzierbare Funktion. Der Gradient
eine differenzierbare Funktion. Der Gradient 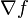 ist ein Funktional, welches Vektoren des
ist ein Funktional, welches Vektoren des 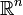 in den Raum der reellen Zahlen abbildet. Auf Differentialformen lautet der Operator
in den Raum der reellen Zahlen abbildet. Auf Differentialformen lautet der Operator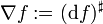 .
.
Da die Menge der 0-Formen nach Definition gleich der Menge der beliebig oft differenzierbaren Funktionen ist, verallgemeinert diese Definition den Gradienten von Funktionen. Dies lässt sich schnell durch eine kurze Rechnung einsehen. Ist
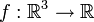 eine glatte Funktion, so gilt
eine glatte Funktion, so giltIn euklidischen Vektorräumen notiert man dies häufig wie folgt:
Rotation
In der Vektoranalysis ist die Rotation eine Abbildung
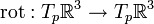 . Für allgemeine Vektorfelder gilt
. Für allgemeine Vektorfelder gilt .
.
Folgende Rechnung zeigt, dass man für die Dimension n = 3 den bekannten Ausdruck für die Rotation erhält:
Diese Formel erhält man sofort, indem man die Definition des Gradienten in die des Kreuzproduktes einsetzt.
Divergenz
Ebenso gibt es eine Verallgemeinerung der Divergenz, diese lautet
Laplace-Beltrami-Operator
Der Laplace-Beltrami-Operator ist eine Verallgemeinerung des Laplace-Operators, welcher in der reellen Analysis und in der Theorie der partiellen Differentialgleichungen untersucht wird. Sei M eine glatte Riemannsche Mannigfaltigkeit, so ist der Laplace-Beltrami-Oprator definiert durch
- Δ = dδ + δd.
Eine Funktion
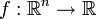 heißt harmonisch, wenn sie die Laplace-Gleichung Δf = 0 erfüllt. Analog definiert man die harmonischen Differentialformen. Eine Differentialform
heißt harmonisch, wenn sie die Laplace-Gleichung Δf = 0 erfüllt. Analog definiert man die harmonischen Differentialformen. Eine Differentialform 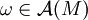 heißt harmonisch, falls die Laplace-Beltrami-Gleichung Δω = 0 erfüllt ist. Mit
heißt harmonisch, falls die Laplace-Beltrami-Gleichung Δω = 0 erfüllt ist. Mit 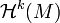 wird die Menge aller harmonischen Formen auf M notiert.
wird die Menge aller harmonischen Formen auf M notiert.Eigenschaften
Der Laplace-Beltrami-Operator hat folgende Eigenschaften:
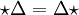 , also falls ω harmonisch ist, so ist auch
, also falls ω harmonisch ist, so ist auch 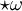 harmonisch.
harmonisch.- Der Operator Δ ist selbstadjungiert bezüglich einer Riemannschen Metrik g, das heißt für alle
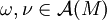 gilt g(Δω,ν) = g(ω,Δν).
gilt g(Δω,ν) = g(ω,Δν). - Notwendig und hinreichend für die Gleichung Δω = 0 ist, dass dω = 0 und δω = 0 gilt.
Dolbeault-Operator
Sei nun M eine komplexe Mannigfaltigkeit der (komplexen) Dimension n und für
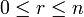 sei
sei  der Vektorraum der komplexwertigen Differentialformen. Eine komplexe r-Form
der Vektorraum der komplexwertigen Differentialformen. Eine komplexe r-Form 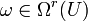 mit
mit  heißt eine (p,q)-Form, wenn
heißt eine (p,q)-Form, wenn 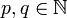 mit p + q = r und ω in lokalen Koordinaten
mit p + q = r und ω in lokalen Koordinaten 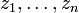 eindeutig geschrieben werden kann als
eindeutig geschrieben werden kann alsDer Kürze und Übersicht wegen definiere
Die äußere Ableitung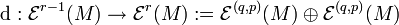 kann man aufspalten in
kann man aufspalten in 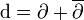 , so dass
, so dassund
in lokalen Koordinaten gilt. Diese Operatoren heißen Dolbeault- und Dolbeault-Quer-Operator (nach Pierre Dolbeault). Um zu erfahren wie diese auf Funktionen (also auf 0-Formen) operieren, siehe unter Wirtinger-Kalkül nach.
Gilt für eine Differentialform
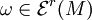 in allen Punkten von M die Gleichung
in allen Punkten von M die Gleichung 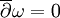 , so spricht man von einer holomorphen Differentialform. Diese haben ähnlich wie die holomorphen Funktionen besondere Eigenschaften. Der Vektorraum der holomorphen Differentialformen auf M wird mit Ω(M) notiert. Aus der Identität
, so spricht man von einer holomorphen Differentialform. Diese haben ähnlich wie die holomorphen Funktionen besondere Eigenschaften. Der Vektorraum der holomorphen Differentialformen auf M wird mit Ω(M) notiert. Aus der Identitätfolgt
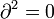 und
und 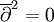 . Diese Operatoren eignen sich also für eine Kohomologietheorie. Diese trägt den Namen Dolbeault-Kohomologie. Außerdem gilt für diese Operatoren eine Leibniz-Regel. Seien
. Diese Operatoren eignen sich also für eine Kohomologietheorie. Diese trägt den Namen Dolbeault-Kohomologie. Außerdem gilt für diese Operatoren eine Leibniz-Regel. Seien 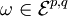 und
und 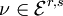 dann gilt
dann giltund
Literatur
- R. Abraham, J. E. Marsden, T. Ratiu: Manifolds, Tensor Analysis, and Applications. Springer-Verlag, Berlin 2003, ISBN 3-540-96790-7.
- S. Morita: Geometry of Differential Forms. American Mathematical Society, ISBN 0-821-81045-6.
- d ist eine Antiderivation, das heißt für
Wikimedia Foundation.

![\begin{array}{rcl}
\mathrm d\omega(X_0,\ldots,X_k)
&=&\sum_{i=0}^k(-1)^{i} X_i\omega(X_0,...,\hat X_i,...,X_k)\\[0.5em]
&+&\sum_{0\leq i<j \leq k}(-1)^{i+j}
\omega([X_i,X_j],X_0,...,\hat X_i,...,\hat X_j,...,X_k)
\end{array}](/pictures/dewiki/101/e5fd3a5b295d97c74987f434d181b978.png)
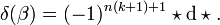
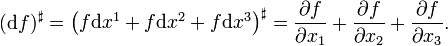
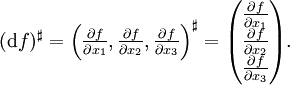
![\begin{array}{cl}
&\mathrm d(f_1\cdot\mathrm dx_1+f_2\cdot\mathrm dx_2 + f_3 \cdot \mathrm{d}x_3)\\
=&\mathrm df_1\wedge\mathrm dx_1+\mathrm df_2\wedge\mathrm dx_2 +\mathrm df_3\wedge\mathrm dx_3 \\[0.5em]
=&\frac{\partial f_1}{\partial x_1}\cdot\mathrm dx_1\wedge\mathrm dx_1 +\frac{\partial f_1}{\partial x_2}\cdot\mathrm dx_2\wedge\mathrm dx_1
+ \frac{\partial f_1}{\partial x_3}\cdot\mathrm dx_3\wedge\mathrm dx_1\\
+&\frac{\partial f_2}{\partial x_1}\cdot\mathrm dx_1\wedge\mathrm dx_2 + \frac{\partial f_2}{\partial x_2}\cdot\mathrm dx_2\wedge\mathrm dx_2
+ \frac{\partial f_2}{\partial x_3}\cdot\mathrm dx_3\wedge\mathrm dx_2\\
+&\frac{\partial f_3}{\partial x_1}\cdot\mathrm dx_1\wedge\mathrm dx_3 + \frac{\partial f_3}{\partial x_2}\cdot\mathrm dx_2\wedge\mathrm dx_3
+ \frac{\partial f_2}{\partial x_3}\cdot\mathrm dx_3\wedge\mathrm dx_3\\[0.5em]
=&\left(\frac{\partial f_3}{\partial x_2} - \frac{\partial f_2}{\partial x_3}\right)\cdot\mathrm dx_2\wedge\mathrm dx_3
+ \left(\frac{\partial f_3}{\partial x_1} - \frac{\partial f_1}{\partial x_3}\right) \cdot\mathrm dx_1\wedge\mathrm dx_3
+ \left(\frac{\partial f_2}{\partial x_1} - \frac{\partial f_1}{\partial x_2}\right)\cdot\mathrm dx_1\wedge\mathrm dx_2
\end{array}](/pictures/dewiki/101/e0af098be054304a5b4a60be4b9baf3c.png)