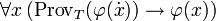Ω-Konsistenz

In der mathematischen Logik wird als ω-konsistent (oder omega-konsistent) eine Theorie bezeichnet, falls sie nicht nur konsistent ist, sondern zusätzlich auch nicht gewisse unendliche Kombinationen von Sätzen beweisen kann, welche intuitiv widersprüchlich sind.

Definition

Sei T eine Theorie, die die Arithmetik interpretiert (d.h. es gibt eine Möglichkeit mit dieser Theorie über natürliche Zahlen zu sprechen). T heißt ω-inkonsistent, falls es eine Eigenschaft P der natürlichen Zahlen gibt, welche in T definierbar ist und T beweist P(0), P(1), P(2), etc. (d.h. T beweist P(n) für jede natürliche Zahl n), aber T beweist auch, dass es eine natürliche Zahl m gibt, so dass P(m) nicht gilt. T heißt ω-konsistent, falls T nicht ω-inkonsistent ist.

Es ist wichtig zu bemerken, dass mit T beweist P(n) für jede natürliche Zahl n nicht die Aussage 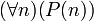$(\forall n )(P(n))$ gemeint ist, sondern die unendliche Menge von Aussagen P(0), P(1), P(2), etc. Daher muss eine ω-inkonsistente Theorie nicht unbedingt inkonsistent sein, da es möglich ist, dass T zwar beweisen kann, dass es ein m gibt, so dass P(m) nicht gilt, aber keinen konkreten Wert für m liefern kann.

Beziehung zu anderen Konsistenzprinzipien

Ist eine Theorie T rekursiv axiomatisierbar, dann kann man nach einem Resultat von C. Smoryński die ω-Konsistenz wie folgt charakterisieren:

T ist ω-konsistent genau dann wenn 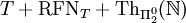$T+\mathrm{RFN}_T+\mathrm{Th}_{\Pi^0_2}(\mathbb N)$ konsistent ist.

Hier bezeichnet 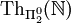$\mathrm{Th}_{\Pi^0_2}(\mathbb N)$ die Menge aller Π⁰₂-Sätze, welche im Standardmodell der Arithmetik gültig sind. RFN_T ist das uniforme Reflexionsprinzip für T, welches aus den Axiomen

$\forall x\,(\mathrm{Prov}_T(\varphi(\dot x))\to\varphi(x))$

für jede Formel $\varphi$ mit einer freien Variable besteht.

Insbesondere ist eine endlich axiomatisierbare Theorie T in der Sprache der Arithmetik ω-konsistent genau dann wenn T+PA 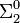$\Sigma^0_2$-korrekt ist.

Beispiel

Bezeichne PA die Theorie der Peano-Arithmetik und Con(PA) sei diejenige arithmetische Aussage, die die Behauptung PA ist konsistent formalisiert. Meist wird Con(PA) von folgender Gestalt sein:

Für jede natürliche Zahl n: n ist nicht die Gödelnummer eines Beweises von 0=1 in PA (d.h. es gibt keinen Beweis des Widerspruchs 0=1)

Auf Grund von Gödels Unvollständigkeitssatz wissen wir, dass falls PA konsistent ist, muss auch PA+¬Con(PA) konsistent sein. PA+¬Con(PA) ist jedoch nicht ω-konsistent aus folgendem Grund: Für jede natürliche Zahl n beweist bereits PA, dass n nicht die Gödelnummer eines Beweises von 0=1 ist, also beweist PA+¬Con(PA) dies sicher auch. Jedoch beweist ¬Con(PA) auch, dass es eine natürliche Zahl m gibt, so dass m die Gödelnummer eines Beweises von 0=1 ist (die ist nämlich gerade die Aussage ¬Con(PA) selber).