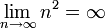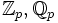- ℝ
-
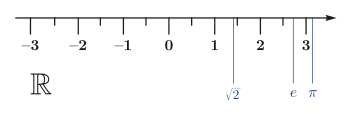
Die Menge der reellen Zahlen ist heute der für Anwendungen der Mathematik wichtigste Zahlbereich: Eine Vielzahl von (berechneten) physikalischen Größen wie zum Beispiel Länge, Temperatur und Masse können mit reellen Zahlen als Maßzahl angegeben werden. Anschaulich entspricht die Menge der reellen Zahlen der Menge aller Punkte der Zahlengeraden. Man sagt: Die reellen Zahlen sind diesen Punkten bijektiv zugeordnet.
Reelle Zahlen sind eine Erweiterung des Bereichs der rationalen Zahlen. Diese Erweiterung ist nötig, weil die rationalen Zahlen für manche Längen keine Maßzahl bereitstellen, zum Beispiel für die Diagonale eines Quadrates mit der Seitenlänge 1 oder für die Teilstrecken in einem Pentagramm mit der Seitenlänge 1. Schon die Pythagoräer erkannten die Notwendigkeit, den Zahlbegriff über die Längenverhältnisse (die durch rationale Zahlen beschrieben werden) hinaus zu erweitern. Erst die moderne Mathematik hat aber den Bereich der reellen Zahlen definiert und damit dem Grenzwertbegriff und der gesamten Analysis ein festes Fundament gegeben.
Für die Menge der reellen Zahlen wird das Symbol
 (auch
(auch 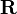 , Unicode ℝ) verwendet. Diese werden unterschieden in:
, Unicode ℝ) verwendet. Diese werden unterschieden in:- Rationale Zahlen -
 = Bruchzahlen der Form ganze Zahl/natürliche Zahl
= Bruchzahlen der Form ganze Zahl/natürliche Zahl
- Ganze Zahlen -
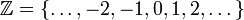 .
.
- Natürliche Zahlen -
 (ohne 0):
(ohne 0):  oder (mit 0):
oder (mit 0): 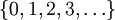 .
.
- Natürliche Zahlen -
- Ganze Zahlen -
- Irrationale Zahlen -
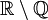 = die Menge aller Elemente von
= die Menge aller Elemente von  , die nicht in
, die nicht in  liegen. Diese lassen sich wiederum in algebraische Zahlen und transzendente Zahlen unterteilen.
liegen. Diese lassen sich wiederum in algebraische Zahlen und transzendente Zahlen unterteilen.
Darstellen lassen sich reelle Zahlen beispielsweise als (unendliche oder abbrechende) Dezimalzahlen.
Inhaltsverzeichnis
Einteilung der reellen Zahlen
Die Menge der reellen Zahlen besteht aus den rationalen Zahlen (ganze Zahlen wie -1, 0, 1, 2 und Bruchzahlen wie 3/4, -2/3 usw.) und den irrationalen Zahlen. Eine Zahl heißt irrational, wenn sie reell, aber nicht rational ist. Die ersten Beweise, dass die Zahlengerade irrationale Zahlen enthält, wurden von den Pythagoräern geführt.
Irrationale Zahlen sind beispielsweise:
- die Kreiszahl π (pi),
- die Eulersche Zahl e,
- die Wurzeln aus ganzen Zahlen, die nicht ganzzahlige Werte haben wie z. B.
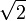 .
.
Eine die rationalen Zahlen umfassende Teilmenge der reellen Zahlen ist die Menge der reell-algebraischen Zahlen, d. h. der reellen Lösungen von Polynomgleichungen mit ganzzahligen Koeffizienten; diese Menge umfasst sämtliche reellen Wurzelausdrücke, aber nicht nur diese (z. B. Lösungen geeigneter Gleichungen 5. Grades). Ihr Komplement ist die Menge der (reellen) transzendenten Zahlen.
Konstruktion von
 aus
aus 
Die Konstruktion der reellen Zahlen als Zahlbereichserweiterung der rationalen Zahlen war im 19. Jahrhundert ein wichtiger Schritt, um die Analysis auf ein solides mathematisches Fundament zu stellen. Die erste exakte Konstruktion geht wohl auf Karl Weierstraß zurück, der die reellen Zahlen über beschränkte Reihen mit positiven Gliedern definierte.[1]
Heute gebräuchliche Konstruktionen der reellen Zahlen:
- Darstellung als Dedekindsche Schnitte rationaler Zahlen: Dabei werden die reellen Zahlen als kleinste obere Schranken von nach oben beschränkten Teilmengen der rationalen Zahlen definiert.[2]
- Darstellung als Äquivalenzklassen von Cauchy-Folgen: Diese heute verbreitetste Konstruktion der reellen Zahlen geht wohl auf Georg Cantor [3] zurück, der die reellen Zahlen als Äquivalenzklassen von rationalen Cauchy-Folgen definierte. Dabei gelten zwei Cauchy-Folgen als äquivalent, wenn ihre (punktweisen) Differenzen eine Nullfolge bilden. Wie man relativ leicht nachprüft, ist diese Relation tatsächlich reflexiv, transitiv und symmetrisch, also zur Bildung von Äquivalenzklassen geeignet.
- Die durch die rationalen Zahlen induzierte Addition und Multiplikation ist wohldefiniert, das heißt unabhängig von der Auswahl des Repräsentanten. Mit diesen wohldefinierten Operationen bilden die reellen Zahlen einen Körper. Ebenfalls durch die rationalen Zahlen wird eine totale Ordnung induziert. Insgesamt bilden die reellen Zahlen damit einen geordneten Körper.
- Darstellung als Äquivalenzklassen von Intervallschachtelungen rationaler Intervalle.[4]
Die drei genannten Konstruktionsmethoden führen zur (bis auf Isomorphie) gleichen Struktur, dem Körper der reellen Zahlen. Jede der Methoden beleuchtet eine andere Eigenschaft der rationalen und reellen Zahlen und ihrer Beziehung zueinander:
- Die Methode der Dedekindschen Schnitte vervollständigt die Ordnung auf den rationalen Zahlen zu einer ordnungsvollständigen Ordnung. Als Ergebnis liegen die rationalen Zahlen (im Sinne der Ordnung) dicht in den reellen Zahlen und jede nach oben beschränkte Teilmenge besitzt ein Supremum.
- Die Methode der Cauchyfolgen vervollständigt die Menge der rationalen Zahlen als metrischer Raum zu einem vollständigen metrischen Raum im topologischen Sinn. Damit liegen die rationalen Zahlen im topologischen Sinn dicht in den reellen Zahlen und jede Cauchy-Folge besitzt einen Grenzwert.
- Die Methode der Intervallschachtelungen reflektiert die numerische Berechnung von reellen Zahlen: Sie werden durch Näherungswerte mit einer gewissen Genauigkeit (Näherungsfehler) approximiert, also in ein Intervall um den Näherungswert eingeschlossen. Der Beweis, dass sich die Näherung (durch iterative oder rekursive Verfahren) beliebig verbessern lässt, ist dann ein Beweis für die „Existenz“ eines reellen Grenzwertes.
Axiomatische Einführung der reellen Zahlen
Die Konstruktion der reellen Zahlen als Zahlbereichserweiterung der rationalen Zahlen wird in der Literatur oft in vier Schritten vorgenommen: Von der Mengenlehre über die natürlichen, die ganzen, die rationalen schließlich zu den reellen Zahlen wie oben beschrieben. Eine direkte Möglichkeit, die reellen Zahlen mathematisch zu erfassen, ist, sie durch Axiome zu beschreiben. Dazu benötigt man drei Gruppen von Axiomen - die Körperaxiome, die Axiome der Ordnungsstruktur sowie ein Axiom, das die Vollständigkeit garantiert.
- Die reellen Zahlen sind ein Körper
- Die reellen Zahlen sind total geordnet (siehe auch geordneter Körper), d. h. für alle reellen Zahlen a,b,c gilt:
- es gilt genau eine der Beziehungen a < b,a = b,b < a (Trichotomie)
- aus a < b und b < c folgt a < c (Transitivität)
- aus a < b folgt a + c < b + c (Verträglichkeit mit der Addition)
- aus a < b und c > 0 folgt ac < bc (Verträglichkeit mit der Multiplikation)
- Die reellen Zahlen sind ordnungsvollständig, d.h. jede nichtleere, nach oben beschränkte Teilmenge von
 besitzt ein Supremum in
besitzt ein Supremum in 
Alternativ kann der Körper der reellen Zahlen auch charakterisiert werden als vollständiger, archimedisch geordneter Körper, d. h. als ein Körper der folgende Axiome erfüllt:
- die Körperaxiome und Ordnungsaxiome
- das Archimedische Axiom:
- Sind a und b positive reelle Zahlen, dann gibt es ein
 , so dass na > b ist.
, so dass na > b ist.
- Sind a und b positive reelle Zahlen, dann gibt es ein
- das Vollständigkeitsaxiom:
- Jede Cauchy-Folge in
 konvergiert oder anders ausgedrückt die reellen Zahlen sind bzgl. der vom Absolutbetrag induzierten Metrik ein vollständiger Raum.
konvergiert oder anders ausgedrückt die reellen Zahlen sind bzgl. der vom Absolutbetrag induzierten Metrik ein vollständiger Raum.
- Jede Cauchy-Folge in
Anstelle des Vollständigkeitsaxioms kann man auch das Intervallschachtelungsaxiom setzen:
- das Intervallschachtelungsaxiom:
- Der Durchschnitt jeder monoton fallenden Folge abgeschlossener beschränkter Intervalle ist nichtleer.
Durch beide Axiomensysteme ist der Körper der reellen Zahlen (bis auf Isomorphie) eindeutig bestimmt.
Wenn man die reellen Zahlen axiomatisch einführt, dann ist die Konstruktion als Zahlbereichserweiterung ihr „Existenzbeweis“, genauer: Die Konstruktion in vier Schritten aus der Mengenlehre beweist, dass ein Modell für die durch die Axiome beschriebene Struktur in der Mengenlehre, von der die Konstruktion ausging, vorhanden ist.
Mächtigkeiten
Die Mächtigkeit von
 wird mit
wird mit  (Mächtigkeit des „Continuums“) oder mit
(Mächtigkeit des „Continuums“) oder mit 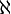 (Aleph) (ohne Index!) bezeichnet. Sie ist größer als die Mächtigkeit der Menge der natürlichen Zahlen, die als kleinste unendliche Mächtigkeit
(Aleph) (ohne Index!) bezeichnet. Sie ist größer als die Mächtigkeit der Menge der natürlichen Zahlen, die als kleinste unendliche Mächtigkeit  heißt. Die Menge der reellen Zahlen ist deshalb überabzählbar. Ein Beweis für ihre Überabzählbarkeit ist Cantors zweites Diagonalargument. Informell bedeutet „Überabzählbarkeit“, dass jede Liste
heißt. Die Menge der reellen Zahlen ist deshalb überabzählbar. Ein Beweis für ihre Überabzählbarkeit ist Cantors zweites Diagonalargument. Informell bedeutet „Überabzählbarkeit“, dass jede Liste 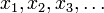 reeller Zahlen unvollständig ist.
reeller Zahlen unvollständig ist.Übliche, weniger umfassende Erweiterungen der Menge der natürlichen Zahlen sind gleichmächtig mit den natürlichen Zahlen, also abzählbar: die Menge der ganzen Zahlen, der rationalen Zahlen und auch der algebraischen Zahlen. Einen Beweis ihrer Abzählbarkeit liefert Cantors erstes Diagonalargument. Die Überabzählbarkeit entsteht also erst durch die Hinzunahme der transzendenten Zahlen.
In der Mengenlehre wurde nach Cantors Entdeckungen die Frage untersucht: "Gibt es eine Mächtigkeit zwischen „abzählbar“ und der Mächtigkeit der reellen Zahlen, zwischen
 und
und  ?" – Oder, für die reellen Zahlen formuliert: "Ist jede überabzählbare Teilmenge der reellen Zahlen gleichmächtig wie die Menge aller reellen Zahlen?" Die Vermutung, dass die Antwort auf die erste Frage „Nein!“ und auf die zweite Frage „Ja“ lautet, wird als Kontinuumhypothese (CH) bezeichnet, kurz formuliert als „
?" – Oder, für die reellen Zahlen formuliert: "Ist jede überabzählbare Teilmenge der reellen Zahlen gleichmächtig wie die Menge aller reellen Zahlen?" Die Vermutung, dass die Antwort auf die erste Frage „Nein!“ und auf die zweite Frage „Ja“ lautet, wird als Kontinuumhypothese (CH) bezeichnet, kurz formuliert als „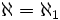 “. Es konnte gezeigt werden, dass die Kontinuumhypothese unabhängig von den üblicherweise verwendeten Axiomensystemen wie der Zermelo-Fraenkel-Mengenlehre mit Auswahlaxiom (ZFC) ist, d.h. sie kann im Rahmen dieser Systeme weder bewiesen noch widerlegt werden.
“. Es konnte gezeigt werden, dass die Kontinuumhypothese unabhängig von den üblicherweise verwendeten Axiomensystemen wie der Zermelo-Fraenkel-Mengenlehre mit Auswahlaxiom (ZFC) ist, d.h. sie kann im Rahmen dieser Systeme weder bewiesen noch widerlegt werden.Topologie, Kompaktheit, erweiterte reelle Zahlen
Die übliche Topologie, mit der die reellen Zahlen versehen werden, ist diejenige, die aus der Basis der offenen Intervalle
![(a,b) = {]a,b[} = \{x \in \R | a &amp;lt; x &amp;lt; b\}](/pictures/dewiki/54/68fae9b8ee43ec519deefa0d4ca26d3b.png) ,
, 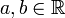 erzeugt wird. In dieser Form geschrieben handelt es sich um die Ordnungstopologie. Offene Intervalle in den reellen Zahlen lassen sich aber auch durch Mittelpunkt und „Radius“ darstellen: ]p − r,p + r[, also als offene Bälle
erzeugt wird. In dieser Form geschrieben handelt es sich um die Ordnungstopologie. Offene Intervalle in den reellen Zahlen lassen sich aber auch durch Mittelpunkt und „Radius“ darstellen: ]p − r,p + r[, also als offene Bälle 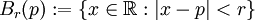 bezüglich der durch die Betragsfunktion definierten Metrik d(x,y): = | x − y | . Die von den offenen Intervallen erzeugte Topologie ist also gleichzeitig die Topologie dieses metrischen Raums. Da die rationalen Zahlen in dieser Topologie dicht liegen, reicht es, sich auf rationale a,b bzw. p,r zu beschränken, die Topologie genügt daher beiden Abzählbarkeitsaxiomen.
bezüglich der durch die Betragsfunktion definierten Metrik d(x,y): = | x − y | . Die von den offenen Intervallen erzeugte Topologie ist also gleichzeitig die Topologie dieses metrischen Raums. Da die rationalen Zahlen in dieser Topologie dicht liegen, reicht es, sich auf rationale a,b bzw. p,r zu beschränken, die Topologie genügt daher beiden Abzählbarkeitsaxiomen.Im Gegensatz zu den rationalen Zahlen sind die reellen Zahlen ein lokalkompakter Raum, zu jeder reellen Zahl x lässt sich also eine offene Umgebung angeben, deren Abschluss kompakt ist. Solch eine offene Umgebung ist einfach zu finden; jede beschränkte, offene Menge U mit
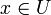 , leistet das Gewünschte: nach dem Satz von Heine-Borel ist
, leistet das Gewünschte: nach dem Satz von Heine-Borel ist 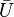 kompakt.
kompakt.Der reelle Zahlenkörper ist nur lokalkompakt, nicht aber kompakt. Eine verbreitete Kompaktifizierung sind die sogenannten erweiterten reellen Zahlen
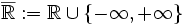 , wobei die Umgebungen von
, wobei die Umgebungen von 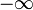 durch die Umgebungsbasis
durch die Umgebungsbasis 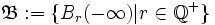 mit
mit  und die Umgebungen von
und die Umgebungen von 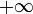 durch die Umgebungsbasis
durch die Umgebungsbasis 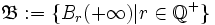 mit
mit 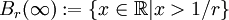 definiert werden. Diese Topologie genügt weiterhin beiden Abzählbarkeitsaxiomen.
definiert werden. Diese Topologie genügt weiterhin beiden Abzählbarkeitsaxiomen.  ist homöomorph zum abgeschlossenen Intervall [0,1], beispielsweise ist die Abbildung
ist homöomorph zum abgeschlossenen Intervall [0,1], beispielsweise ist die Abbildung 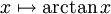 ein Homöomorphismus
ein Homöomorphismus ![\overline{\R}\to[-\pi/2,\pi/2]](/pictures/dewiki/50/2f83a01ac69678821e687af3335d4c1f.png) , und alle kompakten Intervalle sind mittels affin-linearer Funktionen homöomorph. Bestimmt divergente Folgen sind in der Topologie der erweiterten reellen Zahlen konvergent, beispielsweise ist die Aussage
, und alle kompakten Intervalle sind mittels affin-linearer Funktionen homöomorph. Bestimmt divergente Folgen sind in der Topologie der erweiterten reellen Zahlen konvergent, beispielsweise ist die Aussagein dieser Topologie ein echter Grenzwert.
Mit
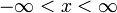 für alle
für alle 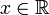 sind die erweiterten reellen Zahlen weiterhin total geordnet; es ist allerdings nicht möglich, die Körperstruktur der reellen Zahlen auf die erweiterten reellen Zahlen zu übertragen, beispielsweise hat die Gleichung
sind die erweiterten reellen Zahlen weiterhin total geordnet; es ist allerdings nicht möglich, die Körperstruktur der reellen Zahlen auf die erweiterten reellen Zahlen zu übertragen, beispielsweise hat die Gleichung 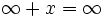 keine eindeutige Lösung.
keine eindeutige Lösung.Verwandte Themen
- Eine näherungsweise Darstellung reeller Zahlen im Computer erfolgt durch Gleitkommazahlen.
- Berechnungen unter Berücksichtigung der Näherungsfehler ermöglicht die Intervallarithmetik.
- Die Darstellung von Zahlen erfolgt in einem Zahlensystem.
Literatur
- Oliver Deiser: Reelle Zahlen - Das klassische Kontinuum und die natürlichen Folgen. Springer-Verlag, 2007, ISBN 3-540-45387-3
- Otto Forster: Analysis 1. Differential und Integralrechnung einer Veränderlichen. 4. Auflage. vieweg, 1983, ISBN 3-528-37224-9
- Harro Heuser: Lehrbuch der Analysis Teil 1. 5. Auflage. Teubner-Verlag, 1988, ISBN 3-519-42221-2
Quellen
- ↑ Georg Cantor. Grundlagen einer allgemeinen Mannigfaltigkeitslehre (1883), §9, zitiert nach Oskar Becker, Grundlagen der Mathematik in geschichtlicher Entwicklung, suhrkamp taschenbuch wissenschaft, 1. Auflage 1995, ISBN 3-518-27714-6, S 245ff.
- ↑ Edmund Landau: Grundlagen der Analysis Chelsea Publ. New York 1948
- ↑ Georg Cantor Grundlagen einer allgemeinen Mannigfaltigkeitslehre (1883), §9, zitiert nach Oskar Becker, Grundlagen der Mathematik in geschichtlicher Entwicklung, suhrkamp taschenbuch wissenschaft, 1. Auflage 1995, ISBN 3-518-27714-6, S 248.
- ↑ Konrad Knopp. Theorie und Anwendung der unendlichen Reihen. 5. Auflage, Springer Verlag 1964, ISBN 3-540-03138-3. §3 Die irrationalen Zahlen.
Weblinks
Natürliche Zahlen
 | Ganze Zahlen
| Ganze Zahlen  | Rationale Zahlen
| Rationale Zahlen  | Reelle Zahlen
| Reelle Zahlen  | Komplexe Zahlen
| Komplexe Zahlen  | Quaternionen
| Quaternionen 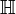 | Oktaven
| Oktaven 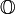
- Rationale Zahlen -
Wikimedia Foundation.