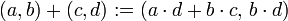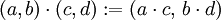- ℚ
-
ℚ
Eine rationale Zahl ist eine Zahl, die als Verhältnis (lateinisch ratio) zweier ganzer Zahlen dargestellt werden kann. Die genaue mathematische Definition beruht auf Äquivalenzklassen von Paaren ganzer Zahlen. Die Menge aller rationalen Zahlen wird mit dem Formelzeichen
 (von „Quotient“) dargestellt.
(von „Quotient“) dargestellt.Inhaltsverzeichnis
Definition
Die Definition der rationalen Zahlen basiert auf der Darstellung rationaler Zahlen durch Brüche, also Paare ganzer Zahlen. Sie ist so aufgebaut, dass das Rechnen mit rationalen Zahlen wie gewohnt mit Hilfe ihrer Bruchdarstellungen durchgeführt werden kann, abstrahiert aber zugleich die rationale Zahl von ihren Bruchdarstellungen. Die rationalen Zahlen werden dabei nicht als vollkommen neue Dinge postuliert, sondern auf die ganzen Zahlen zurückgeführt.
Die Definition beginnt mit der Menge aller geordneten Paare (a,b) ganzer Zahlen bis auf diejenigen Paare, bei denen b = 0. Wichtig: Diese Paare sind nicht die rationalen Zahlen.
Man definiert Addition und Multiplikation auf dieser Menge wie folgt:
Das sind die bekannten Rechenregeln der Bruchrechnung. Die Zahlenpaare kann man damit als Brüche auffassen.
Ein Ziel der Definition rationaler Zahlen ist, dass zum Beispiel die Brüche 2 / 3 und 4 / 6 dieselbe „Zahl“ bezeichnen. Man betrachtet also Brüche, die untereinander äquivalent (von gleichem Wert) sind. Dies wird ausgedrückt durch eine Äquivalenzrelation, die man wie folgt definiert:
-
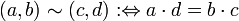 .
.
Wichtig ist, dass diese Relation tatsächlich eine Äquivalenzrelation ist, also die Gesamtmenge in Teilmengen (hier Äquivalenzklassen genannt) untereinander äquivalenter Elemente zerlegt; dies kann man beweisen.
Für die Äquivalenzklassen definiert man wieder Rechenregeln, die auf der Bruchrechnung basieren und dafür sorgen, dass das, was man unter einer rationalen Zahl versteht, von der konkreten Bruchdarstellung abstrahiert wird. Die Addition q + r = s der Äquivalenzklassen q, r und s wird wie folgt definiert:
Aus q wählt man ein beliebiges Element, also ein geordnetes Paar (a,b) ganzer Zahlen (man wählt also ein einziges Element von q und nicht etwa zwei). Ebenso wählt man aus r das Element (c,d).
(a,b) und (c,d) addiert man nun gemäß der Bruchrechnung und erhält ein Paar (e,f). Dieses ist Element einer Äquivalenzklasse s, welche das Ergebnis der Addition ist.
Wichtig ist, dass unabhängig von der konkreten Wahl von (a,b) und (c,d) stets dasselbe Ergebnis, die Äquivalenzklasse s, herauskommt; diese Eigenschaft der Addition muss und kann bewiesen werden.
Analog wird die Multiplikation
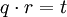 definiert.
definiert.Die Äquivalenzklassen q,r,s,t,... fasst man nun als Elemente einer neuen Menge
 auf und nennt sie rationale Zahlen. Eine einzelne rationale Zahl
auf und nennt sie rationale Zahlen. Eine einzelne rationale Zahl 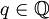 ist also eine unendliche Menge von geordneten Paaren (a,b). Eine Schreibweise wie
ist also eine unendliche Menge von geordneten Paaren (a,b). Eine Schreibweise wie 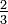 bezeichnet also in diesem Sinne die Äquivalenzklasse aller zu (2,3) äquivalenten Paare.
bezeichnet also in diesem Sinne die Äquivalenzklasse aller zu (2,3) äquivalenten Paare.Man kann dies auch als Zahlbereichserweiterung der ganzen Zahlen auffassen, indem man die ganze Zahl n jeweils mit der rationalen Zahl
 identifiziert. Sind n und m zwei ganze Zahlen und s = n + m,
identifiziert. Sind n und m zwei ganze Zahlen und s = n + m,  deren Summe und Produkt, so sind die Rechenregeln für Brüche gerade so gestaltet, dass
deren Summe und Produkt, so sind die Rechenregeln für Brüche gerade so gestaltet, dass 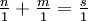 und
und 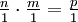 gilt. Außerdem ist vermöge dieser Identifikation ein Bruch in der Tat der Quotient von Zähler und Nenner.
gilt. Außerdem ist vermöge dieser Identifikation ein Bruch in der Tat der Quotient von Zähler und Nenner.Eigenschaften
Die rationalen Zahlen enthalten eine Teilmenge, die zu den ganzen Zahlen
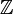 isomorph ist (wähle zu
isomorph ist (wähle zu  die Bruchdarstellung z / 1). Dies wird oft vereinfachend so ausgedrückt, dass die ganzen Zahlen in den rationalen Zahlen enthalten seien.
die Bruchdarstellung z / 1). Dies wird oft vereinfachend so ausgedrückt, dass die ganzen Zahlen in den rationalen Zahlen enthalten seien.Die rationalen Zahlen
 bilden einen Körper.
bilden einen Körper.  ist der kleinste Teilkörper des Körpers
ist der kleinste Teilkörper des Körpers  der reellen Zahlen, also sein Primkörper.
der reellen Zahlen, also sein Primkörper.Eine reelle Zahl ist genau dann rational, wenn sie algebraisch ersten Grades ist. Damit sind die rationalen Zahlen selbst eine Teilmenge der algebraischen Zahlen.
Man kann zeigen, dass
 der kleinste Körper ist, der die natürlichen Zahlen
der kleinste Körper ist, der die natürlichen Zahlen  enthält.
enthält.  ist der Quotientenkörper der ganzen Zahlen
ist der Quotientenkörper der ganzen Zahlen 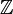 .
.Die rationalen Zahlen liegen dicht auf der Zahlengerade, das heißt: Jede reelle Zahl (anschaulich: jeder Punkt auf der Zahlengerade) kann beliebig genau durch rationale Zahlen angenähert werden.
Trotz der Dichtheit von
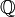 in
in  kann es keine Funktion geben, die nur auf den rationalen Zahlen stetig ist (und damit auf allen restlichen irrationalen Zahlen
kann es keine Funktion geben, die nur auf den rationalen Zahlen stetig ist (und damit auf allen restlichen irrationalen Zahlen 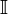 unstetig).
unstetig).Zwischen zwei rationalen Zahlen a und b liegt stets eine weitere rationale Zahl c (und somit beliebig viele). Man nehme einfach das arithmetische Mittel dieser beiden Zahlen:
- c = (a + b) / 2
Was zunächst überraschend klingt, ist die Tatsache, dass die Menge der rationalen Zahlen gleichmächtig zur Menge der natürlichen Zahlen ist. Mit anderen Worten gibt es eine bijektive Abbildung zwischen
 und
und  , die jeder rationalen Zahl q eine natürliche Zahl n zuweist und umgekehrt. Eine mögliche solche bijektive Abbildung liefert Cantors erstes Diagonalargument. Eine weitere liefert das systematische Ordnen aller endlichen Kettenbruchteilnennerfolgen. Eine Liste, die alle rationalen Zahlen zwischen 0 und ½ so (nämlich zuerst nach der Summe aller Teilnenner und dann lexikographisch) ordnet, beginnt folgendermaßen:
, die jeder rationalen Zahl q eine natürliche Zahl n zuweist und umgekehrt. Eine mögliche solche bijektive Abbildung liefert Cantors erstes Diagonalargument. Eine weitere liefert das systematische Ordnen aller endlichen Kettenbruchteilnennerfolgen. Eine Liste, die alle rationalen Zahlen zwischen 0 und ½ so (nämlich zuerst nach der Summe aller Teilnenner und dann lexikographisch) ordnet, beginnt folgendermaßen:1. [0,3] = 1/3 2. [0,2,2] = 2/5 3. [0,4] = 1/4 4. [0,2,1,2] = 3/8 5. [0,2,3] = 3/7 6. [0,3,2] = 2/7 7. [0,5] = 1/5 8. [0,2,1,1,2] = 5/13 9. [0,2,1,3] = 4/11 10. [0,2,2,2] = 5/12 11. [0,2,4] = 4/9 12. [0,3,1,2] = 3/11 13. [0,3,3] = 3/10 14. [0,4,2] = 2/9 15. [0,6] = 1/6 16. [0,2,1,1,1,2] = 8/21 17. [0,2,1,1,3] = 7/18 18. [0,2,1,2,2] = 7/19 19. [0,2,1,4] = 5/14 20. [0,2,2,1,2] = 8/19 21. [0,2,2,3] = 7/17 22. [0,2,3,2] = 7/16 23. [0,2,5] = 5/11 24. [0,3,1,1,2] = 5/18 25. [0,3,1,3] = 4/15 26. [0,3,2,2] = 5/17 27. [0,3,4] = 4/13 28. [0,4,1,2] = 3/14 29. [0,4,3] = 3/13 30. [0,5,2] = 2/11 31. [0,7] = 1/7 32. [0,2,1,1,1,1,2] = 13/34 33. [0,2,1,1,1,3] = 11/29 34. [0,2,1,1,2,2] = 12/31 35. [0,2,1,1,4] = 9/23 36. [0,2,1,2,1,2] = 11/30 37. [0,2,1,2,3] = 10/27 38. [0,2,1,3,2] = 9/25 39. [0,2,1,5] = 6/17 40. [0,2,2,1,1,2] = 13/31 usw. Durch das Hinzufügen des um eins vergrößerten Negativwertes (1 – [0, a, b, c, ...] = [0, 1, a–1, b, c, ...]), dann des Kehrwertes und dann des Negativwertes hinter jede rationale Zahl in dieser Liste und durch Hinzufügen von –1, –½, 0, ½ und 1 entsteht eine bijektive Zuordnung zwischen natürlichen und rationalen Zahlen.
Die Eigenschaft, gleichmächtig zu einer Teilmenge von sich selbst zu sein, ist charakteristisch für unendliche Mengen.
Dezimalbruchentwicklung
Jede reelle Zahl lässt sich einer Dezimalbruchentwicklung zuordnen. Bemerkenswerterweise besitzt jede rationale Zahl eine periodische Dezimalbruchentwicklung, jede irrationale Zahl dagegen eine nichtperiodische (beachte: eine endlich abbrechende Dezimalbruchentwicklung ist ein Spezialfall der periodischen Dezimalbruchentwicklung, bei der sich nach der endlichen Ziffernfolge die Dezimalziffer 0 oder 9 periodisch wiederholt).
Der sich wiederholende Teil wird mit einem Überstrich kenntlich gemacht.
Beispiele sind:
1/3 = 0,3 = 0,33333… = [0,01]2 9/7 = 1,285714 = 1,285714 285714… = [1,010]2 1/2 = 0,50 = 0,50000… = [0,10]2 1 = 1/1 = 1,0 = 0,9 = 1,00000… = 0,99999… = [1,0]2 = [0,1]2 In den eckigen Klammern sind die entsprechenden Entwicklungen im Dualsystem angegeben. Mehrstellige Perioden sind hier jeweils durch Leerzeichen abgetrennt.
Auch die b-adischen Bruchentwicklungen zu anderen ganzzahligen Zahlenbasen
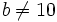 sind für alle rationalen Zahlen periodisch und für alle irrationalen Zahlen nichtperiodisch.
sind für alle rationalen Zahlen periodisch und für alle irrationalen Zahlen nichtperiodisch.Verwandte Themen
- Reelle Zahl
- Irrationale Zahl
- Rationale Funktion
- Bewertungstheorie: p-Bewertung, p-ganze Zahl
- Ordinalzahlen
- Zahlensystem
Natürliche Zahlen
 | Ganze Zahlen
| Ganze Zahlen  | Rationale Zahlen
| Rationale Zahlen  | Reelle Zahlen
| Reelle Zahlen  | Komplexe Zahlen
| Komplexe Zahlen  | Quaternionen
| Quaternionen  | Oktaven
| Oktaven 
-
Wikimedia Foundation.