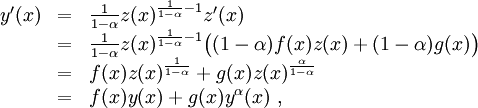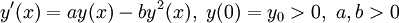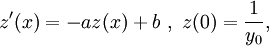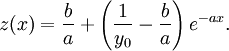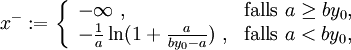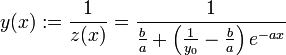Bernoulli-Differenzialgleichung
- Bernoulli-Differenzialgleichung
-
Die bernoullische Differentialgleichung (nach Jakob Bernoulli) ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form
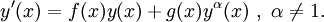
Durch die Transformation
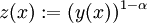
kann man sie auf eine lineare Differentialgleichung zurückführen.
Die Gleichung ist nicht zu verwechseln mit der Bernoulli-Gleichung der Strömungsmechanik.
Satz über die Transformation der bernoullischen Differentialgleichung
Sei 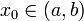 und
und
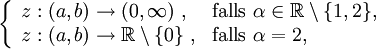
eine Lösung der linearen Differentialgleichung
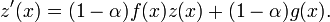
Dann ist
![y(x) := [z(x)]^{\frac{1}{1-\alpha}}](/pictures/dewiki/101/ea51c87d75b36b1c479829dbc4b88cc7.png)
die Lösung der bernoullischen Differentialgleichung
![y'(x) = f(x)y(x) + g(x)y^\alpha(x)\ ,\ y(x_0) = y_0 := [z(x_0)]^{\frac{1}{1-\alpha}}.](/pictures/dewiki/49/18f0ef3c0794ad5e07073dab96c9532f.png)
Weiter besitzt die bernoullische Differentialgleichung für jedes α > 0 trivialerweise 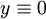 als Lösung für y0 = 0.
als Lösung für y0 = 0.
Beweis
Es gilt
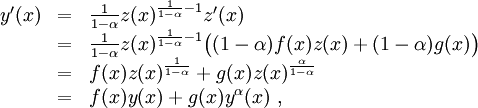
während der Anfangswert trivialerweise erfüllt ist.
Beispiel: Logistische Differentialgleichung
Die logistische Differentialgleichung
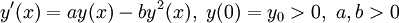
ist eine bernoullische Differentialgleichung mit α = 2. Löst man daher
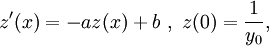
ergibt sich
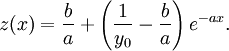
Da z(x) > 0 für alle x > x − mit
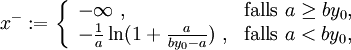
ist
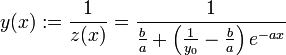
die Lösung obiger Gleichung auf 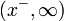 .
.
Literatur
- Harro Heuser: Gewöhnliche Differentialgleichungen, Teubner, März 2004, ISBN 3-519-32227-7
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Differenzialgleichung — Dif|fe|ren|zi|al|glei|chung 〈f. 20; Math.〉 Gleichung zw. den Variablen einer Funktion u. deren Ableitungen; oV 〈fachsprachl.〉 Differentialgleichung * * * Dif|fe|ren|zi|al|glei|chung … Universal-Lexikon
bernoullische Differenzialgleichung — [bɛr nʊli ; nach Jakob und Johann Bernoulli], Bezeichnung für eine gewöhnliche Differenzialgleichung 1. Ordnung der Form y = f(x) · y + g(x) · … Universal-Lexikon
Variationsrechnung — Va|ri|a|ti|ons|rech|nung 〈[va ] f. 20; Math.〉 Verfahren zur Berechnung von Maximal u. Minimalwerten einer Funktion, Teilgebiet der Analysis * * * Variationsrechnung [v ], Teilgebiet der Analysis, das sich mit der Formulierung und Lösung von… … Universal-Lexikon
Tangens Hyperbolicus und Kotangens Hyperbolicus — Graph des Tangens Hyperbolicus Graph des Kotangens Hyperbol … Deutsch Wikipedia
Tangens und Kotangens — Schaubild Tangens (im Bogenmaß) Schaubild Kotangens (im … Deutsch Wikipedia
Riccati — Riccati, Iacopo Francesco Graf, italienischer Privatgelehrter, * Venedig 28. 5. 1676, ✝ Treviso 15. 4. 1754; führte eine umfangreiche philosophische, physikalische und mathematische Korrespondenz und behandelte in zahlreichen Aufsätzen… … Universal-Lexikon
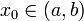 und
und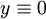 als Lösung für y0 = 0.
als Lösung für y0 = 0.
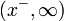 .
.
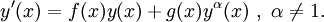
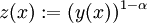
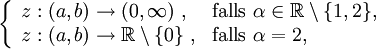
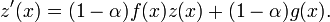
![y(x) := [z(x)]^{\frac{1}{1-\alpha}}](/pictures/dewiki/101/ea51c87d75b36b1c479829dbc4b88cc7.png)
![y'(x) = f(x)y(x) + g(x)y^\alpha(x)\ ,\ y(x_0) = y_0 := [z(x_0)]^{\frac{1}{1-\alpha}}.](/pictures/dewiki/49/18f0ef3c0794ad5e07073dab96c9532f.png)