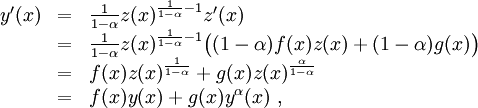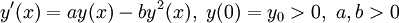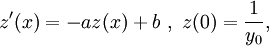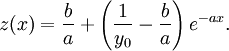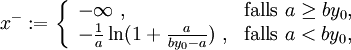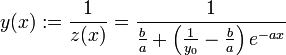Bernoulli-Differentialgleichung
- Bernoulli-Differentialgleichung
-
Die bernoullische Differentialgleichung (nach Jakob Bernoulli) ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form
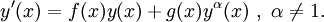
Durch die Transformation
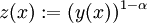
kann man sie auf eine lineare Differentialgleichung zurückführen.
Die Gleichung ist nicht zu verwechseln mit der Bernoulli-Gleichung der Strömungsmechanik.
Satz über die Transformation der bernoullischen Differentialgleichung
Sei 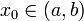 und
und
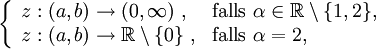
eine Lösung der linearen Differentialgleichung
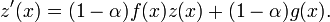
Dann ist
![y(x) := [z(x)]^{\frac{1}{1-\alpha}}](/pictures/dewiki/101/ea51c87d75b36b1c479829dbc4b88cc7.png)
die Lösung der bernoullischen Differentialgleichung
![y'(x) = f(x)y(x) + g(x)y^\alpha(x)\ ,\ y(x_0) = y_0 := [z(x_0)]^{\frac{1}{1-\alpha}}.](/pictures/dewiki/49/18f0ef3c0794ad5e07073dab96c9532f.png)
Weiter besitzt die bernoullische Differentialgleichung für jedes α > 0 trivialerweise 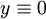 als Lösung für y0 = 0.
als Lösung für y0 = 0.
Beweis
Es gilt
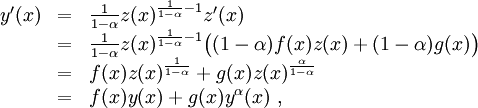
während der Anfangswert trivialerweise erfüllt ist.
Beispiel: Logistische Differentialgleichung
Die logistische Differentialgleichung
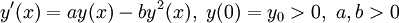
ist eine bernoullische Differentialgleichung mit α = 2. Löst man daher
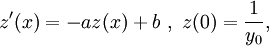
ergibt sich
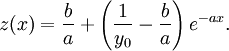
Da z(x) > 0 für alle x > x − mit
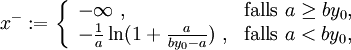
ist
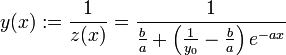
die Lösung obiger Gleichung auf 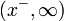 .
.
Literatur
- Harro Heuser: Gewöhnliche Differentialgleichungen, Teubner, März 2004, ISBN 3-519-32227-7
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Bernoulli — ist der Name einer Gelehrtenfamilie, die vom 17. Jahrhundert bis heute viele berühmte Wissenschaftler und Künstler hervorgebracht hat. Als Stammvater wird der niederländische Protestant Leon Bernoulli angesehen, der als Arzt in Antwerpen wirkte.… … Deutsch Wikipedia
Bernoulli-Differenzialgleichung — Die bernoullische Differentialgleichung (nach Jakob Bernoulli) ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form Durch die Transformation kann man sie auf eine lineare Differentialgleichung zurückführen. Die… … Deutsch Wikipedia
Bernoulli-Balken — Die bernoullischen Annahmen sind nach Jakob I. Bernoulli benannte Vereinfachungen der Balkentheorie, die sich als Teilgebiet der Technischen Mechanik mit dem Verhalten belasteter Balken beschäftigt. Die Annahmen Der Balken ist schlank: Die Länge… … Deutsch Wikipedia
Riccati-Differentialgleichung — Die riccatische Differentialgleichung ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form . Sie ist nach dem Mathematiker Jacopo Francesco Riccati benannt, einem italienischen Grafen (1676–1754), der sich intensiv mit… … Deutsch Wikipedia
Jakob I. Bernoulli — Jakob Bernoulli Jakob I. Bernoulli (* 27. Dezember 1654jul./ 6. Januar 1655greg. in Basel; † 16. August 1705 ebenda) war ein Schweizer Mathematiker und Physiker. Die Bezeichnung „Jakob I.“ dient zur Un … Deutsch Wikipedia
Satz von Bernoulli — steht für verschiedene, von Personen aus der Familie Bernoulli aufgestellte, mathematische und physikalische Gesetze, insbesondere: von Daniel Bernoulli Bernoullische Energiegleichung Strömung nach Bernoulli und Venturi von Jakob I. Bernoulli… … Deutsch Wikipedia
Bernoullische Differentialgleichung — Die bernoullische Differentialgleichung (nach Jakob Bernoulli) ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form Durch die Transformation kann man sie auf eine lineare Differentialgleichung zurückführen. Die… … Deutsch Wikipedia
Separierbare Differentialgleichung — Die Methode der Trennung der Veränderlichen (auch Trennung der Variablen, Separationsmethode oder Separation der Variablen) ist ein Verfahren aus der Theorie der gewöhnlichen Differentialgleichungen um Differentialgleichungen erster Ordnung der… … Deutsch Wikipedia
Bernouilli — Bernoulli ist der Name einer Gelehrtenfamilie, die vom 17. Jahrhundert bis heute viele berühmte Wissenschaftler und Künstler hervorgebracht hat. Als Stammvater wird der niederländische Protestant Leon Bernoulli angesehen, der als Arzt in… … Deutsch Wikipedia
Riccati-Gleichung — Die riccatische Differentialgleichung ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form . Sie ist nach dem Mathematiker Jacopo Francesco Riccati benannt, einem italienischen Grafen (1676–1754), der sich intensiv mit… … Deutsch Wikipedia
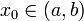 und
und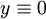 als Lösung für y0 = 0.
als Lösung für y0 = 0.
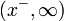 .
.
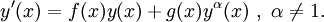
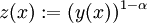
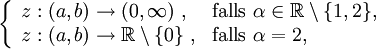
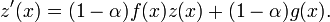
![y(x) := [z(x)]^{\frac{1}{1-\alpha}}](/pictures/dewiki/101/ea51c87d75b36b1c479829dbc4b88cc7.png)
![y'(x) = f(x)y(x) + g(x)y^\alpha(x)\ ,\ y(x_0) = y_0 := [z(x_0)]^{\frac{1}{1-\alpha}}.](/pictures/dewiki/49/18f0ef3c0794ad5e07073dab96c9532f.png)