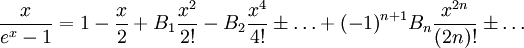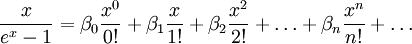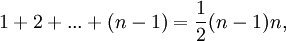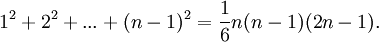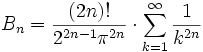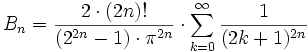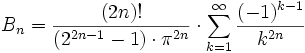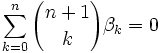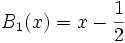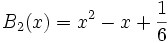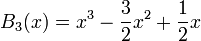Bernoulli-Zahlen

Die Bernoulli-Zahlen B_n sind eine Folge rationaler Zahlen, die in der Mathematik in verschiedenen Zusammenhängen auftreten: als Entwicklungskoeffizienten trigonometrischer, hyperbolischer und anderer Funktionen, in der Euler-Maclaurin-Formel, und in der Zahlentheorie in Zusammenhang mit der Riemannschen Zetafunktion. Die Benennung dieser Zahlen nach ihrem Entdecker Jakob Bernoulli wurde von Abraham de Moivre eingeführt.

Definition

Achtung: In der Literatur werden die Bernoulli-Zahlen in zwei verschiedenen Weisen definiert, die im Folgenden zur Unterscheidung B_n bzw. β_n geschrieben werden.

Die Bernoulli-Zahlen werden am einfachsten als Taylor-Koeffizienten der erzeugenden Funktion 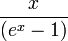$\frac{x}{(e^x-1)}$ eingeführt. Die Reihenentwicklung

$\frac{x}{e^x-1} = 1 - {x\over 2} + B_1 {x^2\over 2!} - B_2{x^4\over 4!} \pm \ldots + {(-1)}^{n+1} B_n {x^{2n}\over (2n)!}\pm \ldots$

beziehungsweise

$\frac{x}{e^x-1} = \beta_0 {x^0\over 0!} + \beta_1 {x\over 1!} + \beta_2 {x^2\over 2!} + \ldots + \beta_n {x^{n}\over n!} + \ldots$

konvergiert für alle x mit einem Betrag kleiner als 2π.

Bernoulli selbst entdeckte diese Zahlen bei der Summation von Potenzen natürlicher Zahlen, z. B.:

$1 + 2 + ... + (n-1) = {1\over 2} (n-1) n,$

$1^2 + 2^2 + ... + (n-1)^2 = {1\over 6} n (n-1) (2n -1).$

Bei der Summation der k-ten Potenzen ist der Koeffizient des linearen Gliedes des Polynoms auf der rechten Seite die Bernoullische Zahl β_k.

Zahlenwerte

Die ersten Bernoulli-Zahlen lauten B₁, B₂, B₃, ... = 1/6, 1/30, 1/42, 1/30, 5/66, 691/2730, 7/6, 3617/510, 43867/798, 174611/330, 854513/138, ... Diese Zahlen finden sich beispielsweise in der Reihenentwicklung des Tangens, Tangens Hyperbolicus oder Cosecans wieder.

In der alternativen Definition ist β₀=1 und β₁=-1/2, alle weiteren β mit ungeradem Koeffizienten verschwinden: β_2n+1=0. Die β mit geraden Koeffizienten ergeben sich aus den B_n gemäß B_n=(-1)ⁿ⁺¹β_2n als β₂, β₄, β₆, ... = 1/6, -1/30, 1/42, -1/30, 5/66, ...

Auch wenn die Folge β_n zunächst kleine Zahlenwerte annimmt, geht |β_n| doch schneller gegen Unendlich als eⁿ. So ist β₁₀₀ ≈ -2.838x10⁷⁸ bzw. β₁₀₀₀ ≈ -5.319x10¹⁷⁶⁹.

Reihenentwicklungen für Bernoulli-Zahlen

Die folgenden Reihenentwicklungen liefern die klassischen (im o.g. Sinne) Bernoulli-Zahlen:

$B_n = \frac{ (2n)!} {2^{2n - 1}\pi ^ {2n}} \cdot \sum_{k=1}^\infty \frac{1}{ k^{2n}}$

$B_n = \frac{ 2 \cdot (2n)!} {(2^{2n} - 1)\cdot\pi ^ {2n}} \cdot \sum_{k=0}^\infty \frac{1}{ (2k + 1) ^{2n}}$

$B_n = \frac{(2n)!} {(2^{2n - 1} - 1)\cdot\pi ^ {2n}} \cdot \sum_{k=1}^\infty \frac{(-1)^{k-1}}{ k^{2n}}$

Rekursionsformel

Setzt man β₀ = 1 und 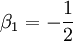$\beta_1 = -\frac{1}{2}$ so ergeben sich die Bernoulli-Zahlen β_k aus der Rekursionformel:

$\sum_{k=0}^n {n + 1\choose k}\beta_k = 0$

Für ungerade Zahlen 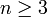$n \ge 3$ gilt β_n = 0.

Bernoulli-Zahlen und Bernoulli-Polynome

Die Bernoulli-Polynome sind eine Abbildung $B_n:[0,1] \rightarrow \mathbb{R}$ und sind durch folgende Rekursionsgleichungen vollständig charakterisiert:

B₀(x) = 1

und für n größer gleich Eins:

$\frac{d}{dx}B_n(x) = n \cdot B_{n-1}(x) \qquad \qquad \int_0^1 B_n(x) \, dx = 0$.

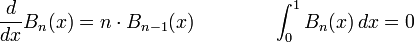Als Summe geschrieben lautet der Ausdruck für das n-te Polynom

$B_n(x) = \sum\limits_{k=0}^n {n\choose k}\beta_k\,x^{n-k}$.

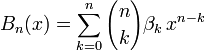Die ersten drei Polynome lauten:

$B_1(x) = x-\frac{1}{2}$

$B_2(x) = x^2 - x + \frac{1}{6}$

$B_3(x) = x^3 -\frac{3}{2}x^2 +\frac{1}{2}x$

Die konstanten Terme dieser Polynome stehen in direktem Zusammenhang mit den Bernoulli-Zahlen, denn es sind gerade die Bernoulli-Zahlen β_n.

Literatur

• J. Neukirch: Algebraische Zahlentheorie. Springer-Verlag, 1992.
• K. Ireland and M. Rosen: A Classical Introduction to Modern Number Theory, Graduate Texts in Mathematics, vol. 84, Springer–Verlag, 2. Auflage 1990.

Weblinks

• Die ersten 498 Bernoulli-Zahlen als Projekt Gutenberg-e-Text.
• Bibliographie für Bernoullizahlen (engl.)
• Weisstein, Eric W. Bernoulli Number From MathWorld