- Bessel'sche Interpolationformel
-
Die Besselsche Interpolationsformel gehört zu den Interpolationsformeln mit äquidistanten Stützstellen. Mit ihrer Hilfe lassen sich Funktionen als Polynome n-ten Grades darstellen. n bestimmt sich aus den n + 1 Stützstellen. Sie wurde nach Friedrich Wilhelm Bessel, ihrem Urheber, benannt.
Differenzentabelle
Zuerst erstellt man eine sog. Differenzentabelle, in der die Interpolationspunkte xi in gleichen Abständen aufeinander folgen. Dieser Abstand h berechnet sich h = xi + 1 − xi. x0 liegt in der Mitte der Stützpunkte. Die Differenzen berechnen sich nun wie folgt: Δfi = f1 + i − fi; alle weiteren analog dazu Δkfi = Δk − 1fi + 1 − Δk − 1fi.
Die Formel
Die Berechnung des Polynoms φ erfolgt dann mit der Formel
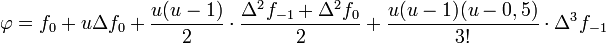
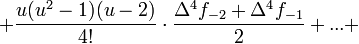
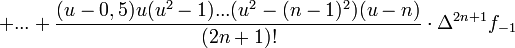 mit
mit 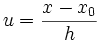 .
.
Wikimedia Foundation.
