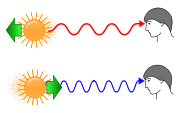
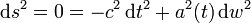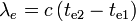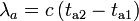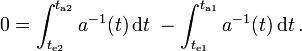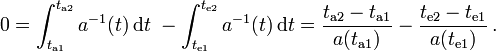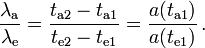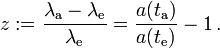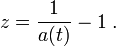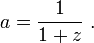Blauverschiebung

Als Rotverschiebung elektromagnetischer Wellen wird die Verlängerung der gemessenen Wellenlänge gegenüber der ursprünglich emittierten Strahlung bezeichnet. Der Effekt ist aus der Astronomie bekannt, wo das Licht weit entfernter Galaxien zum Roten verschoben erscheint. Dies lässt sich durch Analyse der Spektrallinien messen.

Drei Ursachen der Rotverschiebung müssen unterschieden werden:

1. Eine Relativbewegung von Quelle und Beobachter (Dopplereffekt)
2. Ein unterschiedliches Gravitationspotenzial von Quelle und Beobachter (Relativität)
3. Das expandierende Universum zwischen Quelle und Beobachter (Kosmologie)

Rotverschiebung aufgrund einer Relativbewegung

Bewegung einer Lichtquelle relativ zum Beobachter

Wenn ein Beobachter eine sich entfernende Lichtquelle beobachtet, sieht er die Wellenzüge des Lichtes mit geringerer Frequenz, also etwas zum roten Ende des Spektrums verschoben. Dieser Effekt der Relativbewegung von Sender und Empfänger heißt Dopplereffekt. Die Änderung der Frequenz ist proportional zur Geschwindigkeit.

Gravitative Rotverschiebung

Die gravitative Rotverschiebung ist eine direkte Folge der gravitativen Zeitdilatation. Sie ist streng genommen kein Effekt der allgemeinen Relativitätstheorie, sondern folgt bereits aus der speziellen Relativitätstheorie und dem Äquivalenzprinzip der allgemeinen Relativitätstheorie. Licht, das von einer Lichtquelle mit einer gegebenen Frequenz nach oben (also vom Gravitationszentrum weg) ausgestrahlt wird, wird dort mit einer geringeren Frequenz gemessen, ähnlich wie beim Dopplereffekt. Das bedeutet also insbesondere, dass bei einem Lichtsignal mit einer bestimmten Anzahl von Schwingungen der zeitliche Abstand zwischen dem Beginn und dem Ende des Signals beim Empfänger größer ist als beim Sender. Dies wird durch die gravitative Zeitdilatation verständlich.

Gravitative Rotverschiebung einer Lichtwelle

Aufgrund der gravitativen Zeitdilatation ist das Zeitintervall zwischen Anfang und Ende der Lichtwelle umso länger, je weiter nach oben man sich im Gravitationsfeld bewegt, weil die Zeit zunehmend schneller verstreicht. Das bedeutet, dass die Welle bei ihrer Bewegung nach oben immer länger gemessen wird. Daher muss auch der Abstand zwischen den einzelnen Wellenbergen immer mehr wachsen, so dass das Licht also immer langwelliger, also energieärmer erscheint.

Die gravitative Rotverschiebung wurde von Einstein bereits 1911 vor Fertigstellung der allgemeinen Relativitätstheorie vorausgesagt und kann bereits aus der Energieerhaltung hergeleitet werden, so dass ihre experimentelle Bestätigung zwar notwendige Voraussetzung für die Gültigkeit der allgemeinen Relativitätstheorie ist, aber andererseits nicht sehr große Aussagekraft hat. Von W. S. Adams wurde 1925 die Rotverschiebung am Weißen Zwerg Sirius B nachgewiesen. Die Messung der gravitativen Rotverschiebung an weißen Zwergen ist aber schwierig von der Rotverschiebung durch die Eigenbewegung zu unterscheiden, und die Genauigkeit ist begrenzt. Robert Pound und Glen Rebka wiesen 1962 mit Hilfe des Mößbauer-Effektes die gravitative Rotverschiebung der Strahlung einer Gammaquelle im Erdgravitationsfeld bei einem Höhenunterschied von nur 25 m mit ausreichender Genauigkeit nach (Pound-Rebka-Experiment). Spätere Verbesserungen (Pound-Rebka-Snider Experiment) erreichten eine Genauigkeit von etwa 1,5 %. Die gravitative Rotverschiebung wurde mittels Raumsonden auch für die Sonne und den Saturn nachgewiesen. Der geplante Satellit OPTIS soll, neben anderen Tests zu speziellen und allgemeinen Relativitätstheorie, die gravitative Rotverschiebung mit einer Genauigkeit von 10^-5 testen.

Die Entwicklung von Atomuhren hat es möglich gemacht, den Einfluss der Gravitation auf die Zeit auch direkt zu messen. Im Prinzip ist diese Messung eine Variation der Nachweise der gravitativen Rotverschiebung. 1971 wurde durch J. Hafele und R. Keating mit Caesiumuhren in Flugzeugen der durch die Gravitation verursachte Gangunterschied von Uhren in verschiedenen Höhen gemäß der allgemeinen Relativitätstheorie mit etwa 10 % Genauigkeit eindeutig nachgewiesen. Durch ein ähnliches Experiment von C. Alley (Maryland-Experiment) konnte die Genauigkeit 1976 auf 1 % gesteigert werden. R. Vessot und M. Levine publizierten 1979 Ergebnisse eines ähnlichen Experiments mit Hilfe von Raketen und gaben eine Genauigkeit von 0,02 % an. Beim heutigen satellitengestützten GPS-Navigationssystem müssen sowohl Korrekturen gemäß der speziellen als auch der allgemeinen Relativitätstheorie berücksichtigt werden, wobei Effekte durch die allgemeine Relativitätstheorie überwiegen. Umgekehrt kann dies auch als Bestätigung dieser Theorien angesehen werden.

Kosmologische Rotverschiebung

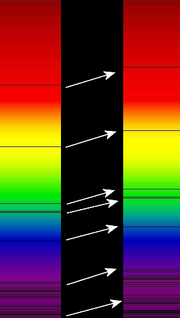Illustration der Rotverschiebung der Spektrallinien für einen weit entfernten Supergalaxienhaufen (BAS11) rechts im Vergleich zur Sonne links

Die Expansion des Universums darf nicht so verstanden werden, dass sich Galaxien in der Raumzeit voneinander entfernen (Relativbewegung). Es ist die Raumzeit selbst, die sich ausdehnt, die Galaxien werden mitbewegt. Eine Expansion gravitativ gebundener Objekte wie Galaxien oder Galaxienhaufen findet nicht statt, denn diese sind durch ihre Eigengravitation von der allgemeinen Expansionsbewegung (beschrieben durch die Friedmann-Gleichungen) entkoppelt. Dies gilt insbesondere auch für Objekte, welche sich innerhalb solcher gravitativ gebundener Systeme befinden (Sterne, Planeten), und auch für elektromagnetisch gebundene Systeme wie Atome und Moleküle. Einer elektromagnetischen Welle hingegen, die sich frei durch eine ausdehnende Raumzeit ausbreitet, wird die Expansionsbewegung direkt aufgeprägt: vergrößert sich die Raumzeit während der Laufzeit um einen Faktor n, so geschieht dies auch mit der Wellenlänge des Lichts.

Diese sogenannte kosmologische Rotverschiebung hängt nicht von der relativen Geschwindigkeit der Galaxien bei der Emission und der Absorption ab. Sie ist von der Rotverschiebung durch den Dopplereffekt, bedingt durch Relativbewegungen der Galaxien im lokalen Gravitationsfeld, zu unterscheiden. Die aus der kosmologischen Rotverschiebung abgeleiteten Fluchtgeschwindigkeiten ferner Galaxien sind demnach direkt auf die Ausdehnung der Raumzeit zurückzuführen. Bereits ab Entfernungen von wenigen 100 Megaparsec ist der Anteil des Dopplereffekts verschwindend gering. Ferner ergibt sich aus der allgemeinen Relativitätstheorie, dass die beobachteten Fluchtgeschwindigkeiten keine relativistischen Zeiteffekte hervorrufen, wie sie von der speziellen Relativitätstheorie für Bewegungen im Raum beschrieben werden. Eine kosmologische Zeitdilatation findet dennoch statt, da die später ausgesandten Photonen eines Objektes aufgrund der Expansion eine größere Wegstrecke zurücklegen müssen. Physikalische Prozesse erscheinen daher bei rotverschobenen Objekten (aus unserer Sicht) zunehmend verlangsamt abzulaufen.

Rotverschiebung und Kosmologie

Das Licht von Galaxien ist in den allermeisten Fällen rotverschoben (bereits unter den nächstgelegenen 1000 sind es etwa ¾). Je weiter eine Galaxie entfernt ist, desto stärker ist im Mittel die Rotverschiebung. Nur wenige - hauptsächlich nahe - Galaxien zeigen aufgrund zusätzlicher Eigenbewegung auf uns zu insgesamt eine Blauverschiebung.

Der Effekt wurde 1929 vom US-Astronomen Edwin Hubble entdeckt, aber zunächst fälschlich als Dopplereffekt interpretiert. Er nimmt mit der Galaxienentfernung gemäß der sog. Hubble-Konstante zu, weshalb man die Entfernungen durch Messung der Rotverschiebung abschätzen kann. Die Rotverschiebung z berechnet sich über

$z =\frac{\lambda_{\mathrm{beobachtet}}-\lambda_0}{\lambda_0}$

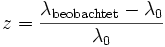
aus der beobachteten Wellenlänge λ_beobachtet und der Wellenlänge λ₀, mit der das Licht ausgesandt wurde. Je höher die Rotverschiebung eines astronomischen Objekts, desto länger war das von ihm ausgesandte Licht unterwegs und desto weiter zurück in der Vergangenheit sehen wir es. Aus der Rotverschiebung kann auch die Entfernung des Objekts bestimmt werden, allerdings ist diese in einer sich ausdehnenden Raumzeit nicht mehr eindeutig definiert. Es gibt verschiedene Entfernungsmaße, die sich aus der Rotverschiebung ableiten lassen. In der Kosmologie werden Betrachtungen und Rechnungen deshalb immer im Rotverschiebungsraum angestellt.

Relativistische Herleitung der kosmologischen Rotverschiebung

Die kosmologische Rotverschiebung beginnt bereits ab Entfernungen von wenigen hundert Megaparsec über die Rotverschiebung durch Relativbewegung (Dopplereffekt) zu dominieren.

Man betrachte ein Photon, emittiert von einer Galaxie mit mitbewegter Entfernung w (siehe auch die relativistische Herleitung der Friedmann-Gleichungen), und absorbiert vom Beobachter bei w = 0. Sowohl die Galaxie als auch der Beobachter folgen der kosmischen Expansion. Orientiert man das beschreibende Koordinatensystem so, dass das Photon entlang dessen polarer Achse läuft, dann lautet das Linienelement des Photons

$\mathrm{d}s^2=0=-c^2\,\mathrm{d} t^2 + a^2(t)\,\mathrm{d} w^2$

wobei c die Lichtgeschwindigkeit darstellt, a(t) den Expansionsfaktor, und w die mitbewegte Radialkoordinate. Zwei aufeinanderfolgende Maxima der Lichtwelle werden zu den kosmologischen Zeiten t_e1 und t_e2 ausgesandt, und zu den Zeiten t_a1 und t_a2 wieder absorbiert. Die Wellenlängen des Photons zu Zeiten der Emission und Absorption sind dann

$\lambda_e=c\,(t_{\mathrm e2}-t_{\mathrm e1})$

$\lambda_a=c\,(t_{\mathrm a2}-t_{\mathrm a1})$

Die mitbewegte Entfernung, die von beiden Maxima zurückgelegt wird, ist per Definition gleich groß. Integriert man das Linienelement des Photons, so erhält man

$0 = \int_{t_{\mathrm{e2}}}^{t_{\mathrm{a2}}} a^{-1}(t)\,{\mathrm{d}} t\; - \int_{t_{\mathrm{e1}}}^{t_{\mathrm{a1}}} a^{-1}(t)\,{\mathrm{d}} t\,.$

Durch Vertauschen der Integrationsgrenzen ergibt sich dann für infinitesimal kleine Intervalle zwischen Emission (Absorption) der beiden Maxima

$0 = \int_{t_{\mathrm a1}}^{t_{\mathrm a2}} a^{-1}(t)\,{\mathrm{d}} t\; - \int_{t_{\mathrm e1}}^{t_{\mathrm e2}} a^{-1}(t)\,{\mathrm{d}} t = \frac{t_{\mathrm a2}-t_{\mathrm a1}}{a(t_{\mathrm a1})} - \frac{t_{\mathrm e2}-t_{\mathrm e1}}{a(t_{\mathrm e1})}\,.$

Unter Verwendung der emittierten und absorbierten Wellenlängen wie sie oben angegeben sind, kann man deren Verhältnis ableiten,

$\frac{\lambda_{\mathrm a}}{\lambda_{\mathrm e}} = \frac{t_{\mathrm a2}-t_{\mathrm a1}}{t_{\mathrm e2}-t_{\mathrm e1}} = \frac{a(t_{\mathrm a1})}{a(t_{\mathrm e1})}\,.$

Schließlich definiert man dann die kosmologische Rotverschiebung zu

$z := \frac{\lambda_{\mathrm a}-\lambda_{\mathrm e}}{\lambda_{\mathrm e}} = \frac{a(t_{\mathrm a})}{a(t_{\mathrm e})}-1\,.$

Da für die meisten Zwecke der Absorptionszeitpunkt t_a mit der heutigen Zeit t = t₀ zusammenfällt und a(t₀) = 1, ergibt sich vereinfacht

$z=\frac{1}{a(t)}-1\;.$

Umgekehrt ergibt sich hieraus unmittelbar der Skalenfaktor des Universums zum Emissionszeitpunkt im Vergleich zum heutigen Wert,

$a=\frac{1}{1+z}\;.$

Beobachtet man beispielsweise eine Galaxie mit Rotverschiebung z = 3, so hatte das Universum zum Zeitpunkt der Aussendung des von uns empfangenen Lichts nur ein Viertel seiner Größe. Sämtliche physikalischen Prozesse in dieser Galaxie laufen aus der Sicht des Beobachters um einen Faktor (1 + z) = 4 verlangsamt ab, da sich der Abstand zweier nacheinander emittierter Photonen entsprechend vergrößert, und damit auch deren Eintreffen beim Beobachter (kosmologische Zeitdilatation). Ein bekanntes Beispiel hierfür ist die zunehmende Streckung der Lichtkurven von Supernovae vom Typ Ia, deren Zustandekommen gut verstanden ist, mit wachsender Rotverschiebung.

Messmethoden

In der Astronomie wird die Rotverschiebung durch Methoden der Spektralanalyse gemessen; sie sind heute durch digitale statt fotografische Erfassung wesentlich genauer geworden. Doch um Spektrallinien gut erfassen zu können, müssen die Galaxien eine gewisse Mindest-Helligkeit aufweisen. Rotverschiebungen von Galaxien werden im Rahmen von Durchmusterungen wie dem Sloan Digital Sky Survey regelmäßig neu bestimmt.

In der Chemie können Rotverschiebungen mit dem Mößbauer-Effekt besonders genau gemessen werden, weil die Ausprägung der Elektronenhülle eines Moleküls auf die Energieniveaus seiner Atomkerne zurückwirkt. Siehe hierzu Mößbauerspektroskopie.

Siehe auch

• Sachs-Wolfe-Effekt
• Stokesverschiebung

Weblinks

• Licht und Asche des Urknalls (aus: Sterne und Weltraum, Special 2 - Schöpfung ohne Ende, S. 106-117)