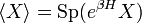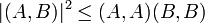Bogoliubov Ungleichung

Dieser Artikel wurde aufgrund von inhaltlichen Mängeln auf der Qualitätssicherungsseite des Portals Physik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Physik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Hilf mit, die inhaltlichen Mängel dieses Artikels zu beseitigen, und beteilige dich an der Diskussion.

Die Bogoliubov-Ungleichung ist eine allgemeine Aussage in der statistischen Physik. Sie beschreibt eine Beziehung zwischen Erwartungswerten von quantenmechanischen Operatoren im thermischen Gleichgewicht. Veröffentlicht wurde sie 1962^[1] von dem russischen Physiker und Mathematiker Nikolai Nikolajewitsch Bogoljubow.

Inhalt

Betrachtet wird ein physikalisches System beschrieben mittels eines Hamiltonoperators H. Dann gilt für zwei Operatoren A und C (für die die angegebenen Mittelwerte existieren, die aber ansonsten beliebig sind):

$|\langle[C,A]\rangle|^2\leq\frac{\beta}{2}\langle\{A,A^\dagger\}\rangle\langle[C^\dagger,[H,C]]\rangle\qquad \text{mit} \qquad \beta=\frac{1}{k_B T}$

wobei [A,C] als Kommutator, sowie {A,C} als Anti-Kommutator zu verstehen sind, sowie der Erwartungswert eines Operators X als

$\langle X \rangle = \text{Sp}(e^{\beta H}X)$

gegeben ist. k_B ist die Boltzmann-Konstante. Der (ursprüngliche) Beweis des Mermin-Wagner-Theorems beruht hauptsächlich auf dieser Ungleichung.^[2]

Beweisidee

Der Beweis der Bogoliubov-Ungleichung basiert darauf, dass über

$(A,B)=\sum^{E_n\neq E_m}_{nm}\langle n|A^\dagger|m\rangle \langle m|B|n\rangle\frac{e^{-\beta E_m}-e^{-\beta E_n}}{E_n-E_m}$

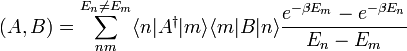
ein positiv semi-definites Skalarprodukt definiert ist. Als Skalarprodukt erfüllt es die Schwarzsche Ungleichung:

$|(A,B)|^2\leq (A,A)(B,B)$

Betrachtet man nun $B=[C^\dagger,H]$ so erhält man die Ungleichung.

Literatur

• Nolting Quantentheorie des Magnetismus, Teubner, Bd.2

Quellen

1. ↑ N. N. Bogoliubov, Physik. Abhandl. Sowjetunion 6, 1, 113, 229 (1962)
2. ↑ Mermin, Wagner Absence of ferromagnetism or antiferromagnetism in 1 or 2 dimensional isotropic Heisenberg models, Physical Review Letters, Bd.17, 1966, S.1133