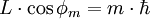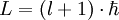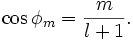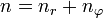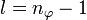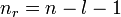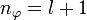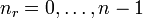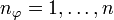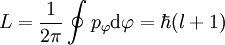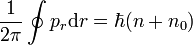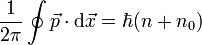Bohr-Sommerfeld-Modell

Das bohr-sommerfeldsche Atommodell, sommerfeldsche Atommodell oder die Sommerfeld-Erweiterung ist eine physikalische Beschreibung der Elektronenbahnen in einem Atom. Es wurde 1915/16 von Arnold Sommerfeld vorgeschlagen und stellt eine Verfeinerung des bohrschen Atommodells dar.

Überblick

Wie das bohrsche ist auch das bohr-sommerfeldsche Modell eine alte Quantentheorie. Es wird angenommen, dass sich die Elektronen um den Atomkern auf Bahnen bewegen, die sich aus den Bewegungsgleichungen der klassischen Mechanik ergeben. Quantentheoretische Prinzipien werden durch zusätzliche Quantisierungsbedingungen (Bohr-Sommerfeld-Quantisierung) eingeführt. Diese Quantisierungsbedingungen führen dazu, dass nur eine kleine Teilmenge der Bahnen, die nach der klassischen Mechanik möglich wären, erlaubt sind. Als Folge davon können auch die mit der Bahnbewegung verbundenen Erhaltungsgrößen (Energie, Drehimpuls) nicht mehr beliebige, sondern nur noch bestimmte, diskrete Werte annehmen. Diese sind also "gequantelt".

Obwohl die Vorstellung von definierten Teilchenbahnen in der Quantenmechanik um 1925 zugunsten von bloßen Wahrscheinlichkeitsverteilungen (Orbitalen) aufgegeben wurde, bleibt das bohr-sommerfeldsche Atommodell wegen seiner Anschaulichkeit von hohem didaktischem Wert; es reicht aus, um qualitativ den Aufbau des Periodensystems der chemischen Elemente zu erklären.

Geometrie der Elektronenbahnen

Während im Modell von Bohr die möglichen Bahnen des Elektrons Kreise um den Atomkern sind, führt Sommerfeld allgemeinere Ellipsenbahnen ein, der Kreis kommt noch als Spezialfall der Ellipse vor. Der Kern befindet sich nach diesem Modell in einem der Brennpunkte einer Bahnellipse, so dass sich eine geometrische Konfiguration wie bei den Planetenbahnen nach den keplerschen Gesetzen ergibt. Auf den Ellipsen bewegt sich das Elektron wie auf den bohrschen Bahnen ohne Emission elektromagnetischer Strahlung, wie sie nach der klassischen Elektrodynamik auftreten müsste.

Das Bohr-Sommerfeldsche Modell stellt also ein keplersches Planetensystem im Kleinen dar, während das bohrsche der älteren kopernikanischen Vorstellung entspricht. Die Analogie zur Planetenbewegung um die Sonne ist naheliegend, da die Kraftfelder der Coulombkraft des Atomkerns und der Gravitation der Sonne die gleiche Form haben: die Kraft F ist proportional zum reziproken Abstandsquadrat:

$F \sim { 1 \over r^2 }$.

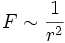Quantenzahlen

Eine Ellipse kann nicht mehr wie ein Kreis durch einen Parameter (Radius) beschrieben werden, sondern dazu benötigt man zwei (z. B. große und kleine Halbachse). Deshalb sind bei Ellipsenbahnen auch zwei Quantenzahlen notwendig, um den Bahnparameter und damit den Zustand des Atoms zu beschreiben.

• die Hauptquantenzahl n wird aus dem bohrschen Modell übernommen, ist aber nicht mehr mit einem bestimmten Drehimpuls verbunden, sondern gibt nur noch das Energieniveau an.
• hinzu kommt die Neben- oder (Bahn-)Drehimpulsquantenzahl l, deren Wertebereich von der Hauptquantenzahl n abhängt, in dem sich das Atom befindet; l kann als Werte Natürliche Zahlen von 0 bis n-1 annehmen.

Diese beiden Quantenzahlen reichen, um eine Ellipse in der Ebene zu beschreiben. Um die Lage der Ellipsenebene im dreidimensionalen Raum zu kennzeichnen, führte Sommerfeld noch eine weitere Quantenzahl ein

• die magnetische Quantenzahl m. Der Wertebereich dieser Quantenzahl ist abhängig davon, welche Nebenquantenzahl l das Elektron gerade hat, m kann die Werte -l,...,-1,0,1,...,+l annehmen.

Neben diesen im bohr-sommerfeldschen Atommodell eingeführten Quantenzahlen gibt es auch noch die Spinquantenzahl s, welche die Rotationsrichtung – rechts herum oder links herum - also den Spin angibt. Sie wird mit den Werten +½ oder -½ beziehungsweise den Symbolen ↑ oder ↓ angegeben. Diese Quantenzahl resultiert aber nicht aus Sommerfelds Quantisierungsbedingungen, sondern wurde später aufgrund experimenteller Befunde (z.B. Stern-Gerlach-Versuch) ins Modell eingefügt.

Nebenquantenzahl

Elektronenbahnen für Wasserstoff im bohr-sommerfeldschen Atommodell für n=1,2,3; Skalenwerte in Ångström.

Während im bohrschen Modell mit der Hauptquantenzahl n sowohl Bahndrehimpuls als auch Energieniveau eindeutig festgelegt sind, gilt dies im Bohr-Sommerfeld Modell nur für die Energie. Zu einer Hauptquantenzahl n gibt es hier n verschiedene Bahnen mit jeweils einem eigenen Bahndrehimpuls, der durch die Neben- oder Drehimpulsquantenzahl festgelegt ist.

In der geometrischen Betrachtung wird jede erlaubte Kreisbahn im bohrschen Modell, welche durch die Hauptquantenzahl n charakterisiert ist, durch ein System von Ellipsen ersetzt, wobei die Zahl der Ellipsen gleich n ist. Jede Ellipse entspricht genau einem Drehimpuls, mit der Drehimpulsquantenzahl l werden die Ellipsen des Systems in der Weise durchnummeriert, dass l=0 die am meisten gestreckte Ellipse (größte numerische Exzentrizität) und l=n-1 einem Kreis, welcher der bohrschen Bahn entspricht, ist. Die große Halbachse einer Ellipse ist gleich dem Radius der Kreisbahn im Bohr-Modell.

Für den Betrag des Bahndrehimpulses L im Bohr-Sommerfeld-Modell gilt:

$L = (l+1) \hbar$.

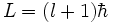Dieses Ergebnis weicht von den Ergebnissen der späteren Quantenmechanik ab. Dort lautet der Zusammenhang:

$L = \sqrt{l(l+1)}\hbar$.

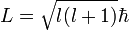Dabei ist 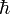$\hbar$ die plancksche Konstante h geteilt durch 2π.

Magnetische Quantenzahl

Das sich um den Atomkern bewegende Elektron erzeugt ein statisches Magnetfeld 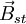$\vec B_{st}$, dessen Richtung (Feldvektor) senkrecht auf der Bahnellipse steht bzw. parallel zum Bahndrehimpulsvektor 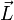$\vec L$ verläuft. Bringt man das Atom in ein äußeres Magnetfeld 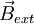$\vec B_{ext}$, dann richtet sich die Bahn des Elektrons so aus, dass sein Feldvektor bzw. Bahndrehimpulsvektor mit dem des äußeren Feldes nur bestimmte diskrete Winkel 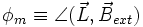$\phi_{m} \equiv \angle (\vec L, \vec B_{ext})$ einschließen, der durch die magnetischen Quantenzahl beschrieben ist. Für einen vorgegebenen Bahndrehimpuls 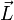$\vec L$ gilt:

$L \cdot \cos \phi_{m} = m \cdot \hbar$

Da für den Drehimpuls gilt (siehe Abschnitt: Nebenquantenzahl)

$L = (l + 1) \cdot \hbar$

gilt für die möglichen eingeschlossenen Winkel bei vorgegebener Nebenquantenzahl l:

$\cos \phi_{m} = {m \over {l+1}} .$

Da sich m im Wertebereich von -l,...,0,...l bewegt, ist der Kosinus immer kleiner 1 bzw. bleibt der Betrag des eingeschlossenen Winkels kleiner als ein rechter Winkel.

Spinquantenzahl

Einem Elektron kann auf jeder Bahn entweder der Spin +1/2 oder -1/2 zugeordnet werden. Jede bisher genannte Bahn kann durch diese beiden Spins in zwei Bahnen unterschiedlicher Energie aufgespalten werden.

Pauli-Verbot

Hauptartikel: Pauli-Prinzip

Zwei Elektronen dürfen in einem Atom nicht in allen Quantenzahlen übereinstimmen.

Radiale und azimutale Quantenzahl

Statt n und l werden auch zwei andere Quantenzahlen verwendet, die radiale Quantenzahl n_r und die azimutale Quantenzahl 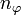$n_\varphi$. Diese resultieren direkt aus der Bohr-Sommerfeld-Quantisierung. Die Quantenzahlen können nach folgenden Formeln ineinander umgerechnet werden:

$n = n_r + n_\varphi\,$

$l = n_\varphi - 1\,$

$n_r = n - l - 1\,$

$n_\varphi = l + 1\,$

Die Wertebereiche sind:

$n_r = 0, \ldots , n-1\,$

$n_\varphi = 1, \ldots , n\,$

Verbesserung gegenüber dem bohrschen Atommodell

Der Fortschritt des bohr-sommerfeldschen Atommodells gegenüber seinem Vorgänger besteht vor allem darin, dass es die Feinstruktur des Wasserstoffspektrums erklären kann und berechenbar macht. Dies ist möglich, wenn man Effekte berücksichtigt, die aus der speziellen Relativitätstheorie folgen. Diese Effekte bewirken, dass die Bahnen keine geschlossenen Ellipsenbahnen mehr sind, sondern Rosettenbahnen (Analogie zur Periheldrehung des Merkur im Sonnensystem). Die Effekte sind umso stärker, je größer die numerische Exzentrizität der Ellipse ist. Dies führt weiterhin dazu, dass die Energie auch vom Bahndrehimpuls abhängt, also die unterschiedlichen Bahnen zu einer Hauptquantenzahl nun nicht mehr exakt das gleiche Energieniveau haben. Dies ist die Ursache für die Feinstruktur der Spektrallinien: untersucht man bestimmte Spektrallinien genauer, stellt man deshalb fest, dass diese in Wirklichkeit aus dicht beeinanderliegenden Linien besteht, die zu unterschiedlichen Werten der Drehimpulsquantenzahl l bei gleicher Hauptquantenzahl n gehören.

Mathematische Darstellung

Mathematisch dargestellt sieht die Quantisierung des Drehimpulses folgendermaßen aus:

$L = \frac{1}{2 \pi} \oint p_\varphi \mathrm d \varphi = \hbar (l+1)$

Die zweite Quantisierungsregel lautet

$\frac{1}{2 \pi} \oint p_r \mathrm d r = \hbar (n + n_0)$

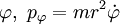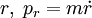Hier sind jeweils $\varphi,\;p_\varphi=mr^2\dot\varphi$ und $r,\;p_r=m\dot r$ Paare von kanonisch konjugierten Orts- und Impulsvariablen. Das n₀ ist eine Korrektur die aber nicht analytisch ermittelt werden kann, sondern aus Näherungsverfahren (etwa WKB-Methode) berechnet werden muss. Für den harmonischen Oszillator etwa ist 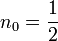$n_0 = \frac{1}{2}$ und sichert hierbei die von Null verschiedene Grundzustandsenergie. Die angegebenen Integrale über einen geschlossenen Weg im Phasenraum (aufgespannt durch die Orts- und Impulskoordinaten) sind quantisiert und können nur Vielfache der Planck-Konstante 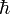$\hbar$ annehmen.

Durch Addition erhält man die Form

$\frac{1}{2 \pi} \oint \vec p \cdot \mathrm d \vec x = \hbar (n + n_0)$

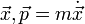wobei $\vec x,\vec p=m\dot{\vec x}$. Diese Form ist sogar invariant unter kanonischen Transformationen.

Siehe auch

• Elektronenkonfiguration
• Elektronenhülle