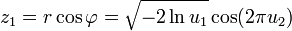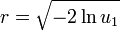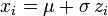Box-Muller-Verfahren

Graphische Veranschaulichung der Box-Muller-Methode

Die Box-Muller-Methode (nach George Edward Pelham Box und Mervin Edgar Muller 1958) ist ein Verfahren zur Erzeugung normalverteilter Zufallszahlen.

Idee

Bei dieser Methode werden zunächst zwei Standardzufallszahlen u₁ und u₂ benötigt. Diese lassen sich beispielsweise mit einem Zufallszahlengenerator erzeugen. Standardzufallszahlen unterliegen einer Rechteckverteilung mit den Parametern 0 und 1.

Erzeugung standardnormalverteilter Zufallszahlen

Es lässt sich zeigen, dass man nach folgendem Transformationsschritt daraus zwei standardnormalverteilte (stochastisch) unabhängige Zufallszahlen z₁ und z₂ erhält:

$z_1 = r \cos \varphi = \sqrt{-2 \ln u_1} \cos ( 2 \pi u_2 )$

und

$z_2 = r \sin \varphi = \sqrt{-2 \ln u_1} \sin ( 2 \pi u_2 )$.

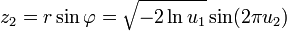Hierbei wurde die Inversionsmethode zur Transformation von u₁ und u₂ in die Polarkoordinaten r und $\varphi$ ausgenutzt:

$r = \sqrt{-2 \ln u_1}$

und

$\varphi = 2 \pi u_2$.

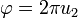Bei der Anwendung der Inversionsmethode wurde berücksichtigt, dass bei Polarkoordinaten $\varphi$ einer Rechteckverteilung mit den Parametern 0 und 2π unterliegt und r einer Exponentialverteilung mit dem Parameter $\tfrac{1}{2}$.

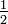Die bisherigen Transformationsschritte erzeugen zwei standardnormalverteilte Zufallszahlen. Eine Standardnormalverteilung ist ein Spezialfall der Normalverteilung, nämlich mit dem Erwartungswert μ = 0 und der Varianz σ² = 1.

Um mit der Box-Muller-Methode Normalverteilungen mit beliebigen Parametern zu erzeugen, lassen sich die erhaltenen z_i nach dem Muster

$x_i = \mu + \sigma\,z_i$

transformieren. In der obigen Notation steht π wie üblich für die Kreiszahl, sin für den Sinus, cos für den Kosinus und ln für den natürlichen Logarithmus.

Probleme

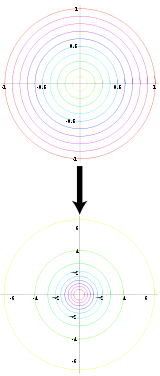
Verwendet man zur Erzeugung der u_i einen linearen Kongruenzgenerator, so liegen die Paare (z₁;z₂) auf einer durch eine Spirale beschriebenen Kurve. Dieses Verhalten ist eng mit dem im Satz von Marsaglia beschriebenen Hyperebenenverhalten linearer Kongruenzgeneratoren verwandt.

Dieses Problem lässt sich umgehen, wenn statt des linearen Kongruenzgenerators ein inverser Kongruenzgenerator verwendet oder die Polar-Methode verwendet wird.

Fazit

Die Box-Muller-Methode erzeugt zunächst zwei stochastisch unabhängige und standardnormalverteilte Zufallszahlen, die sich dann in eine Normalverteilung mit beliebigen Parametern transformieren lassen.

Die Box-Muller-Methode erfordert die Auswertung von Logarithmen und trigonometrischen Funktionen, was auf einigen Rechnern sehr zeitaufwendig sein kann.

Alternativen

Weitere Möglichkeiten zur Erzeugung normalverteilter Zufallszahlen sind im Artikel Normalverteilung beschrieben.

Eine Alternative ist z.B. die Polar-Methode.^[1]

Quellen und Fußnoten

1. ↑ siehe Kinderman, A.J. und J.R. Ramage: Computer Generation of Normal Random Numbers, Jour. Amer. Stat. Assoc., 71(356), p. 893-896 (1976)

Literatur

• George Edward Pelham Box, Mervin Edgar Muller: A note on the generation of random normal deviates. Ann. Math. Stat. 29. 1958) 610-611.
• Donald Ervin Knuth: The Art of Computer Programming, Sec. 3.4.1, p. 117
• O. Moeschlin, O., E. Grycko, C. Pohl und F. Steinert: Experimental Stochastics. Springer, 1998, ISBN 3-540-14619-9, Kapitel 1.4 Generating Sample Values