- Black-Box-Modell
-
Die Regelungstechnik ist ein Gebiet der Ingenieurwissenschaft und Teilgebiet der Automatisierungstechnik. Sie befasst sich mit der gezielten Beeinflussung von physikalischen, chemischen, biologischen oder anderen Größen in Geräten, Anlagen, Fahrzeugen mittels des Prinzips der Rückkopplung, so dass das Verhalten dieser Größen einem gewünschten Verhalten möglichst nahe kommt. Sie nutzt eine systematische, mathematische Darstellung[1][2][3]. Dabei ist häufig die vollständige Automatisierung eines solchen Vorgangs möglich, jedoch muss gelegentlich auch menschliche Tätigkeit aus technischen und/oder wirtschaftlichen Gründen zum Vorgang beitragen (Elementares Beispiel: Einstellen einer angenehmen Duschwassertemperatur, komplexeres Beispiel: Lenken eines Passagierflugzeugs). Die Regelungstechnik stützt sich stark auf die Denkweisen und Methoden der mathematischen Systemtheorie mit Denkmodellen wie z. B. das dynamische System. Das heute als Regelungstechnik bezeichnete Gebiet entstand Mitte des 20. Jahrhunderts unter dem weiter gefassten Begriff der Kybernetik. Grundlegende Ergebnisse der modernen Regelungstheorie wurden u. a. von Norbert Wiener, Rudolf Kálmán und David G. Luenberger beigetragen.
 Dreitanksystem zur Erprobung von regelungstechnischen Methoden, wie es in Lehre und Forschung häufig eingesetzt wird. Die zwei äußeren Tanks werden von Pumpen mit Wasser befüllt. Je zwei Ventilwege verbinden die äußeren mit dem mittleren Tank. Eine typische Aufgabe ist die Regelung des mittleren Behälterfüllstands. Störungen (Schwankungen des Füllstands) werden durch einen variablen Abfluss erzeugt. Sie müssen von einer Regelung ausgeglichen werden.
Dreitanksystem zur Erprobung von regelungstechnischen Methoden, wie es in Lehre und Forschung häufig eingesetzt wird. Die zwei äußeren Tanks werden von Pumpen mit Wasser befüllt. Je zwei Ventilwege verbinden die äußeren mit dem mittleren Tank. Eine typische Aufgabe ist die Regelung des mittleren Behälterfüllstands. Störungen (Schwankungen des Füllstands) werden durch einen variablen Abfluss erzeugt. Sie müssen von einer Regelung ausgeglichen werden.Inhaltsverzeichnis
Überblick
Ziele und Aufgabengebiete
Das Ziel der Regelungstechnik ist die zielgerichtete Veränderung des Verhaltens eines Systems, um ihm gewünschte Eigenschaften aufzuprägen[2][3]. Diese Eigenschaften können vielfältig sein, zum Beispiel:
- Sollwertfolge / Festwertregelung: Der Ausgang des geregelten Systems entspricht nach Abklingen des Übergangsverhaltens (transientes Verhalten) genau dem von außen vorgegebenen konstanten Sollwert. Dieses Ziel wird durch eine Festwertregelung erreicht, wobei sich der Sollwert von Zeit zu Zeit ändern kann. Er muss jedoch mit Bezug auf die größte Zeitkonstante der Regelstrecke hinreichend lange konstant bleiben, so dass das Übergangsverhalten abklingen kann.
- Trajektorienfolge: Der Ausgang folgt einer dynamischen Sollwerttrajektorie genau (Folgeregler). Dieses Ziel kann durch einen bestimmten Regler nur für eine bestimmte Klasse von Sollwertsignalen gelöst werden, da der Regler in Bezug auf diese Signalklasse entworfen wird (z. B. konstante Signale, sprungförmige Signale, rampenförmige Signale, sinusförmige Signale).
- Störunterdrückung: Der Ausgang (z. B. Raumtemperatur bei der Raumtemperaturregelung) soll von einer äußeren Störgröße (z. B. Außentemperatur) unbeeinflusst sein.
- Robustheit: Die drei genannten Eigenschaften müssen auch dann gegeben sein, wenn die reale Regelstrecke nicht genau mit dem Modell übereinstimmt. Man spricht von Robustheit gegen Modellunsicherheiten.
Je nach Ziel ist eine spezifische Vorgehensweise bei der Bestimmung des Reglers erforderlich. Die Aufgaben der Regelungstechnik gehen jedoch über die reine Regelung hinaus. Eine Auswahl von typischen Aufgaben sind
- Stabilisierung einer instabilen Regelstrecke,
- Regulierung auf einen Festwert,
- Trajektorienfolge mit/ohne Anforderungen an das dynamische Übergangsverhalten,
- Störentkopplung zur Unterdrückung von äußeren und inneren Störgrößen,
- Anlagenüberwachung zum Feststellen von Fehlern und Ausfällen (Fehlerdiagnose) sowie der Vermeidung gefährlicher Betriebszustände. Siehe auch fehlertolerantes Regelsystem.
Zur Lösung dieser Aufgaben bedient sich die Regelungstechnik mathematischer Methoden der Systemtheorie. Diese Methoden gliedern sich weiter in den Entwurf von Reglern, Kompensatoren und Überwachungseinrichtungen, sowie die Analyse der Regelstrecke sowie des resultierenden Gesamtsystems.
Bezüge zu benachbarten Fachgebieten
Regelungstechnik hat als interdisziplinäres Gebiet Berührungspunkte mit zahlreichen anderen Fachgebieten, vor allem der Messtechnik, Mathematik und Informatik. Zu den vielfältigen Anwendungsbereichen zählen die Fertigungstechnik, Medizintechnik, Verfahrenstechnik, Verkehrstechnik, Robotik, aber auch Wasserwirtschaft und Soziologie. Typische Anwendungen sind Autopiloten in Luftfahrt und Schifffahrt oder Antiblockiersystem und Tempomat in der Kraftfahrzeugtechnik. Auch im Bereich der Biologie gibt es natürliche Regelkreise.
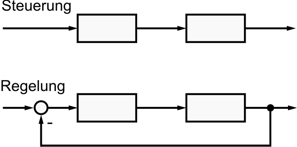
Unterschied zwischen Regelung und Steuerung
- Begriffsklärung: Regelung (Regelungstechnik)
Bei der Regelung wird der tatsächliche Wert des Ausgangs auf den Regler zurückgeführt, so dass Störungen automatisch ausgeglichen werden. Die DIN 19226 definiert den Begriff der Regelung wie folgt:
„Das Regeln, die Regelung, ist ein Vorgang, bei dem fortlaufend eine Größe, die Regelgröße (zu regelnde Größe), erfasst, mit einer anderen Größe, der Führungsgröße, verglichen und im Sinne einer Angleichung an die Führungsgröße beeinflusst wird. Kennzeichen für das Regeln ist der geschlossene Wirkungsablauf, bei dem die Regelgröße im Wirkungsweg des Regelkreises fortlaufend sich selbst beeinflusst. “
– Deutsches Institut für Normung: DIN 19226 Teil 1
Ist der fortlaufende Vergleich nicht vorhanden, spricht man von einer Steuerung. Eine Heizung, die nur die Außentemperatur misst und aufgrund deren Wert den Raum beheizt ist eine Steuerung. Das Heizen hat auf die Außentemperatur keinen Einfluss. Es wird also nichts rückgeführt.
Der Regelkreis
- Hauptartikel: Regelkreis
Standardregelkreis
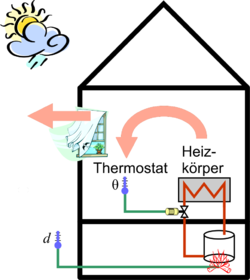
Bevorzugter Untersuchungsgegenstand der Regelungstechnik ist der Regelkreis. Als einfaches, anschauliches Beispiel soll hier die Regelung einer Raumtemperatur dienen.
Ziel ist das selbsttätige Halten der Raumtemperatur auf einem gewünschten Wert, obwohl durch das Öffnen des Fensters und Änderungen der Außentemperatur eine variable Wärmemenge aus dem Raum abgeführt wird. Am Thermostatventil wird die gewünschte Solltemperatur des Raumes eingestellt. Das Ventil verändert den Warmwasserstrom durch den Heizkörper und damit die Raumtemperatur. Der Sensor des Thermostatventiles misst die aktuelle Temperatur θ (Theta) und verändert die Ventilstellung.
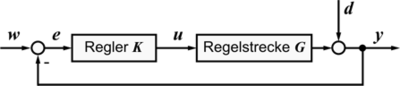
Zusätzlich wird durch Anhebung der Vorlauftemperatur des Warmwassers auf eine Veränderung der Außentemperatur reagiert, bevor diese im Raum spürbar ist. Diese Störgrößenaufschaltung verbessert das Regelverhalten, ist aber nicht Bestandteil des Standardregelkreises im folgenden Blockschaltbild:
Zeichen Funktion Bedeutung im Beispiel K Regler Thermostatventil G Regelstrecke Heizung und Zimmer w Sollwert
auch FührungsgrößeSolltemperatur z. B. 22 °C e Regeldifferenz
e = w − yz. B. 2 °C u Stellwert Ventilhub des Heizungsventils d Störgröße Temperaturänderung durch das offene Fenster oder die Außentemperatur y Regelgröße
auch Istwertaktuelle Raumtemperatur θ z. B. 20 °C Damit das Verhalten des Regelkreises berechnet werden kann, wird er im Blockschaltbild in einzelne Funktionsblöcke zerlegt. Jedes Rechteck steht für eine mathematische Beschreibung des Verhaltens des Teilsystems. Die Pfeile zeigen den Signalverlauf. Mit Methoden der Systemtheorie kann das gesamte Verhalten berechnet und optimiert werden. Hier dient das Blockschaltbild zur Erklärung der Funktion.
Die Regeldifferenz e ist die Differenz zwischen Sollwert w und Istwert y. Sie wird vom Regler in einen Stellwert u gewandelt der über die Regelstrecke den Istwert y beeinflusst. Dadurch ergibt sich ein neuer Istwert der die Regeldifferenz verkleinert.
Entscheidendes Merkmal des Regelkreises ist die negative Rückkopplung (Gegenkopplung) der Regelgröße auf den Regler. Diese Eigenschaft ist wichtig für die Stabilität des Regelkreises. Im Beispiel bedeutet eine Gegenkopplung, dass eine zu hohe Temperatur zum Schließen des Heizungsventils führt und nicht zum Öffnen.
Das Thermostatventil ist Sensor, Regler und Aktor in einem Gerät. Durch Drehen des Einstellrades wird ein Sollwert vorgegeben. Die Flüssigkeit des Temperatursensors im Thermostatventil dehnt sich bei Erwärmung aus und bildet den Istwert. Diese Dehnung wird direkt auf den Ventilhub als Stellgröße übertragen (P-Regler). Dadurch verringert sich der Warmwasserstrom durch den Heizkörper. Nach einer Verzögerung sinkt die Temperatur im Raum. Durch richtige Wahl des Reglers und der Einstellungen können in industriellen Regelkreisen diese Verzögerungen verkürzt oder ganz ausgeglichen werden.
Erweiterung der Regelkreisstruktur
Der Standardregelkreis kann je nach Problem verfeinert werden. Häufig wird die Regelstrecke weiter in Stellglieder (Aktoren) und die eigentliche Regelstrecke unterteilt. Zur besseren Unterdrückung von Störgrößen kann ein Störgrößenmodell aufgestellt und deren Einfluss durch eine Störgrößenaufschaltung vermindert werden[2]. Im Beispiel oben durch Anhebung der Vorlauftemperatur des Warmwassers.
In einigen regelungstechnischen Anwendungen ist es erforderlich, mehrere Regler zu komplexen Regelstrukturen zu verschalten. Die wichtigsten Strukturen sind:
- Kaskadenregelung
- Verhältnisregler
- Mischungsregler
- Begrenzungsregler
- Splitrange-Regelung
Systemmodelle und Modellbildung
Modelle bilden die analytische Grundlage für die Analyse des Verhaltens von Regelstrecke, Regelkreis und für die meisten systematischen Reglerentwurfsverfahren. Eine Ausnahme bilden die Einstellregeln.
Lineare und nichtlineare Systeme
Eine grundlegende Unterscheidung bietet das Linearitätskriterium. Ein lineares System erlaubt die Anwendung des Überlagerungsprinzips. Besonders einfach sind lineare, zeitinvariante Systeme (LZI-System, engl. LTI für linear time-invariant). Für die Klasse der LZI-Systeme existiert eine Vielzahl von Methoden zu Analyse und Reglerentwurf. Die Theorie nichtlinearer Systeme ist weitaus komplexer, daher werden nichtlineare Systeme oft linearisiert. Hierzu gibt es zwei wesentliche Möglichkeiten, zum einen die Linearisierung im Arbeitspunkt, zum anderen die Methode der globalen Linearisierung.
Lineare Modellformen
Lineare gewöhnliche Differentialgleichungen sind die grundlegende zeitkontinuierliche Modellform im Zeitbereich. Lineare gewöhnliche Differenzengleichungen sind ihre zeitdiskrete Entsprechung. Durch Einführung von Hilfsvariablen gelangt man zum zeitkontinuierlichen oder zeitdiskreten Zustandsraummodell (ZRM), in dem nur Ableitungen erster Ordnung auftreten. Das Zustandsraummodell beschreibt das gesamte dynamische Verhalten des modellierten Systems einschließlich seiner internen Größen, die nicht messbar sind und daher nicht Teil des Ausgangs sind. Damit verwandt ist das Deskriptor-System.
Durch Laplace-Transformation (eine Integraltransformation) der ursprünglichen zeitkontinuierlichen gewöhnlichen Differentialgleichung oder des Zustandsraummodells gelangt man zur Darstellung der Übertragungsfunktion. Sie ist eine Frequenzbereichsdarstellung, die ausschließlich das Eingangs-/Ausgangsverhalten wiedergibt, aber keine Aussagen über die Bewegung interner Größen erlaubt. Nach Laplace-Transformation lässt sich das System algebraisch behandeln, was gegenüber der Darstellung als Differentialgleichung eine große Vereinfachung darstellt. In der Regelungstechnik wird die Übertragungsfunktion der Regelstrecke meist mit G(s) bezeichnet, für Mehrgrößensysteme ist sie eine Matrix. Für weitere Details, siehe Regelkreis.
Die zeitdiskrete Frequenzbereichsdarstellung erhält man durch Anwendung der Z-Transformation auf Differenzengleichung oder das zeitdiskrete Zustandsraummodell. Sie ermöglicht eine zur Laplace-Transformierten sinngemäße Behandlung des Systems.
Die Übertragungsfunktion der offenen Kette Go(s) setzt sich aus der Übertragungsfunktion aller Glieder im Vorwärtszweig (Strecke G(s) und Regler K(s)) zusammen. Die Führungsübertragungsfunktion Gw(s) ergibt sich aus der Rückkopplung (Gegenkopplung) der Ausgangsgröße über die Messeinrichtung (Gm(s)) auf den Regler. Wird Gw(s) bei kleinen Frequenzen betrachtet, so ergibt sich die bleibende Regeldifferenz des Systems. Ist Gw(s = 0) = 1 dann ist die bleibende Regeldifferenz e gleich null. Zur Veranschaulichung der Übertragungsfunktion von LZI-Systemen wird häufig das Bodediagramm verwendet.
Blockschaltbilder und Signalflusspläne mit kontinuierlichen oder diskreten Signalgliedern werden zur graphischen Veranschaulichung verwendet. Da sie eine graphische Darstellung mathematischer Modelle sind, gibt es Regeln zur Analyse und Umformung von Blockschaltbildern bzw. Signalflussplänen. Die Grundgleichungen für Übertrager werden graphisch in regelungstechnischen Blöcken dargestellt. Die gebräuchlichsten Übertragungsglieder (Proportional-Glied (P), Integral-Glied (I), Differential-Glied (D), PT1-Glied, PT2-Glied usw.) lassen sich auch mit einfachen Operationsverstärkerschaltungen realisieren.
Nichtlineare Modellformen
Ausgangspunkt sind nichtlineare gewöhnliche Differentialgleichungen, aus denen wiederum ein Zustandsraummodell gewonnen werden kann. Es unterscheidet sich von linearen ZRM nur durch die rechte Seite, die nun nicht mehr durch lineare Abbildungen, sondern nichtlineare Abbildungen bestimmt ist. Zwei einfache Spezialfälle sind das Hammerstein-Modell und das Wiener-Modell, bei denen sich die Nichtlinearität auf eine statische Kennlinie beschränkt.
Eine spezielle Klasse nichtlinearer Systeme ist die Klasse der hybriden Systeme. Ein hybrides System weist Sprünge in den Zustandsvariablen und ein Umschalten der Dynamik auf. Hybride Systeme entstehen typischerweise durch die Kopplung kontinuierlicher dynamischer Systeme mit ereignisdiskreten Systemen.
Modellbildung
Die Modellbildung beschreibt den Vorgang des Abbildens von Teilstücken der Realität. Das Modell stellt ein abstraktes Abbild eines Systems dar, welches stellvertretend für das System untersucht wird. Zur Ermittlung eines mathematischen Modells für ein gegebenes System können die physikalische Modellbildung, die Systemidentifikation oder Mischformen aus beiden Vorgehensweisen angewandt werden:
- In der physikalische Modellbildung werden grundlegende physikalische Beziehungen zum Aufstellen eines analytischen Systemmodells genutzt[2][3]. Diese Beziehungen resultieren einerseits aus der Anwendung von Erhaltungssätzen, beispielsweise für Masse, Energie und Drehimpuls. Daraus werden Koppelbeziehungen zwischen den Komponenten des Systems erhalten. Andererseits sind Gleichungen zur Beschreibung der Komponenten erforderlich, wie z. B. das ohmsche Gesetz zur Beschreibung des Spannungsabfalls über einem Widerstand oder das Gesetz der turbulenten Strömung nach Torricelli. Die Modellparameter sind durch physikalische Konstanten sowie die Eigenschaften der Komponenten vorgegeben, die zum Teil aus Datenblättern ermittelt werden können, andernfalls geschätzt werden müssen. In Anlehnung an den englischen Sprachgebrauch wird diese Vorgehensweise auch als White-Box-Modellierung oder strukturelle Modellbildung bezeichnet.
- Die Systemidentifikation erstellt ein mathematisches Systemmodell unter ausschließlicher Verwendung von Messwerten des Eingangs-/Ausgangsverhaltens[4][5][6]. Die innere physikalische Struktur des Systems ist nicht von Interesse. Dieser Ansatz wird in Anlehnung an den englischen Sprachgebrauch als Black-Box-Modellierung oder pragmatische Modellbildung bezeichnet.
- Mischform: Häufig wird die physikalischen Modellbildung nur zur Ermittlung der Struktur und dynamischen Ordnung des Modells eingesetzt. Insbesondere sind die Parameter nur teilweise durch Naturkonstanten und Datenblätter gegeben. In diesem Fall wird die Parameterschätzung zur Ermittlung fehlender Modellparameter eingesetzt. Dazu sind experimentelle Daten des Eingangs-/Ausgangsverhaltens erforderlich. Dieser Ansatz wird in Analogie zur Black-Box- und White-Box-Modellierung als Grey-Box-Modellierung bezeichnet, um zum Ausdruck zu bringen, dass das Vorwissen über das Modell begrenzt ist.
Analyse des Kreisverhaltens
Stabilität
- Hauptartikel: Stabilitätstheorie
Die Stabilität des Regelkreises ist eine grundlegend wichtige Eigenschaft, da in der Praxis Instabilität meist zu Schäden führt (z. B. Absturz eines Flugzeuges, Explosion eines Kessels usw.). Grundlegende Erkenntnisse zur Stabilitätstheorie wurden von Maxwell, Routh und Hurwitz beigetragen.
Zur Beurteilung der Stabilität eines Regelkreises existieren mehrere Stabilitätsbegriffe und dazugehörige Analysemethoden, welche die Stabilitätstheorie bilden. Grundvoraussetzung für die Stabilitätsprüfung ist, dass ein mathematisches Modell der Regelstrecke vorliegt.
Gängige Stabilitätsbegriffe sind die Zustandsstabilität und Eingangs-/Ausgangs-Stabilität (E/A-Stabilität). Die Zustandsstabilität fordert anschaulich, dass alle Zustandsvariablen ohne äußeren Einfluss auf ein Gleichgewicht zustreben. Bei LZI-Systemen ist dies der Ursprung, bei nichtlinearen Systemen kann es mehrere Gleichgewichtszustände geben. Zur ihrer Analyse ist die Eigenbewegung des Systems maßgeblich. Die E/A-Stabilität (auch BIBO-Stabilität, engl. bounded input-bounded output) fordert lediglich, dass die Ausgangssignale bei beschränkten Eingangssignalen und verschwindendem Anfangszustand beschränkt bleiben.
Im Fall von LZI-Systemen kann für die Betrachtung der Stabilität auf die charakteristische Gleichung zurückgegriffen werden, welche das charakteristische Polynom verwendet. Liegen bei zeitkontinuierlichen Systemen alle Eigenwerte, das heißt Lösungen der charakteristischen Gleichung, in der linken Halbebene der komplexen s-Ebene, so ist der Regelkreis stabil. Weitere Kriterien zur Prüfung der Stabilitätseigenschaft für LZI-Systeme sind das Hurwitzkriterium, das Phasenrandkriterium und das Nyquistkriterium.
Ein sehr allgemeines, auch für nichtlineare Systeme geeignetes Kriterium zur Stabilitätsprüfung ist die direkte Methode von Ljapunov anhand der Ljapunov-Funktion (Ljapunov-Methode). Weitere für nichtlineare Systeme anwendbare Stabilitätskriterien sind das Popov-Kriterium[7] und das Kreiskriterium[8].
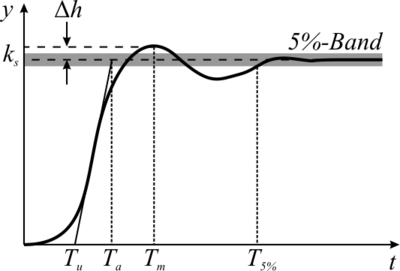 Kenngrößen des Verhaltens eines dynamischen Systems, dargestellt anhand der Sprungantwort. Die Verzugszeit Tu und Anstiegszeit Ta sind durch die Wendetangente bestimmt. Die Überschwingzeit Tm ist durch den Zeitpunkt, an dem das erste Maximum der Sprungantwort auftritt festgelegt. Die Beruhigungszeit T5% ist der letzte Zeitpunkt, zu dem die Sprungantwort in ein Band der Breite ±5% eintaucht.
Kenngrößen des Verhaltens eines dynamischen Systems, dargestellt anhand der Sprungantwort. Die Verzugszeit Tu und Anstiegszeit Ta sind durch die Wendetangente bestimmt. Die Überschwingzeit Tm ist durch den Zeitpunkt, an dem das erste Maximum der Sprungantwort auftritt festgelegt. Die Beruhigungszeit T5% ist der letzte Zeitpunkt, zu dem die Sprungantwort in ein Band der Breite ±5% eintaucht.Sollwertfolge
Die Sollwertfolge kann anhand der Übertragungsfunktion des geschlossenen Kreises überprüft werden. Die Frequenz Null muss mit der Verstärkung eins übertragen werden, dann ist Sollwertfolge gewährleistet.
Dynamisches Übergangsverhalten
Unter dem dynamischen Übergangsverhalten werden Anforderungen an das Kreisverhalten zusammengefasst, die seine Geschwindigkeit und sein Überschwingen betreffen (siehe Abbildungen). Sie werden anhand der Übergangsfunktion definiert. Die Überschwingzeit Tm bezeichnet den Zeitpunkt des ersten Überschwingmaximums der Sprungantwort. Die Zeit T5% bezeichnet die Zeit, nach der die Sprungantwort ein Band der Breite ±5% nicht mehr verlässt. Die Überschwingweite bezeichnet die Amplitude der Schwingung einer Sprungantwort um den statischen Endwert. Weitere Kenngrößen sind die Verzugszeit Tu und die Anstiegszeit Ta.
Weitere gebräuchliche Maße für die Güte des Regelverhaltens sind Integralkriterien, die geeignet sind, die Güte des Regelverhaltens in Abhängigkeit von den durch die Sprungantwort und die Führungsgröße abgegrenzten Flächen abzuschätzen. Ein solches Gütekriterium ist das ITAE-Kriterium.
Bestimmung des Reglers
Gegenstand dieses Kapitels ist die Ermittlung eines geeigneten Reglers, so dass die oben genannten Anforderungen an den Regelkreis erfüllt werden. Der Regler kann dabei eine von vielfältigen Strukturen annehmen, siehe Regler. Hier soll jedoch nur eine Übersicht über die Entwurfsverfahren gegeben werden. Die meisten Entwurfsverfahren sind für vielfältige Reglerstrukturen anwendbar.
Heuristische Einstellregeln
- Hauptartikel: Faustformelverfahren (Automatisierungstechnik)
Unter dem Begriff der Einstellregeln, auch Faustformelverfahren genannt, werden heuristische, aber systematische Verfahren zur Auswahl der Reglerstruktur und Festlegung der Reglerparameter zusammengefasst. Vorteilhaft ist die Unabhängigkeit von detaillierten mathematischen Systemmodellen. Der Schritt der Modellbildung kann somit entfallen. Stattdessen müssen wenige Kennwerte der Regelstrecke bekannt sein, die aus einfachen Versuchen ermittelt werden. Hingegen können keine scharfen Güteforderungen an das Kreisverhalten gestellt werden. Genügt die heuristisch erreichte Güte nicht, so muss zu einem modellbasierten Entwurf übergegangen werden. Die verschiedenen Einstellregeln unterscheiden sich hinsichtlich der Grundannahmen, die bezüglich der zu regelnden Strecke getroffen werden.
Linearer Reglerentwurf
Unter Entwurf wird hier eine systematische Vorgehensweise verstanden, die ein mathematisches Systemmodell zur Grundlage hat. Ein besonderes Merkmal jener Entwurfsmethoden sind Garantien über die erreichte Güte. Diese Garantien gelten innerhalb des Bereichs der LZI-Systeme. Sie sind nur beschränkt auf die Praxis übertragbar, da lineare Systeme nur eine Abstraktion und Vereinfachung darstellen und jedes reale System in irgendeiner Form davon abweicht. Bei Perturbationsmodellen werden die am Modell ermittelten Eigenschaften auch in der Praxis gut erreicht, wenn nur geringe Abweichungen vom Arbeitspunkt auftreten.
Zeitkontinuierliche Regelung
Zum Reglerentwurf für lineare zeitinvariante Systeme existieren u. a. folgende Entwurfsverfahren.[2][3]
Das Wurzelortskurvenverfahren ist ein Verfahren für Eingrößensysteme im Frequenzbereich. Es nutzt die Wurzelortskurve, um die offene Kette zielgerichtet so zu verändern, dass die Pole des geschlossenen Kreises in einem gewünschten Zielgebiet liegen. Das Zielgebiet ergibt sich anhand der Güteforderungen im Zeitbereich.
Das Frequenzkennlinienverfahren ist ebenfalls ein Verfahren für Eingrößensysteme im Frequenzbereich. Das Werkzeug zum Entwurf ist das Bodediagramm. Die Güteforderungen aus dem Zeitbereich werden in Anforderungen an die Form des Amplituden- und Phasengangs der offenen Kette aus Regler und Strecke übersetzt. Anschließend wird der dynamische Regler schrittweise so aufgebaut, dass die erforderlichen Formparameter des Amplituden- und Phasenganges erreicht werden. Die Methode ist für Mehrgrößensysteme anwendbar, wenn diese schwach verkoppelt sind (Direktes Nyquistverfahren). Die schwache Kopplung äußert sich in einer Diagonaldominaz der Systemmatrix, die ggf. durch ein zusätzliches Entkopplungsglied hergestellt wird.
Die Optimalregler-Verfahren verwenden mathematische Optimierungstheorie, um den Regler so zu bestimmen, dass ein Gütekriterium an die Bewegung des Ausganges und die erforderliche Stellenergie erfüllt ist. Das Verfahren ist für Mehrgrößensysteme geeignet. Dazu wird als Gütekriterium ein Funktional formuliert, in das der Regelfehler und die Stellgröße eingehen. Ziel der Optimierung ist die Minimierung des Gütefunktionals, so dass der integrale Regelfehler und die erforderliche Stellenergie minimal sind. Die Gewichtung von Regelfehler und Stellenergie kann durch Wichtungsmatrizen beeinflusst werden. Häufig wird ein quadratisches Gütekriterium verwendet, man spricht dann von einem LQ-Regler (von engl. linear quadratic regulator). Da zum Entwurf eine Riccatigleichung bzw. -differentialgleichung zu lösen ist, ist auch der Begriff Riccatiregler gebräuchlich.
Beim Reglerentwurf zur Polvorgabe (engl. pole placement) geht typischerweise von einer Darstellung im Zustandsraum aus. Die Güteforderungen aus dem Zeitbereich werden in die Lage der Eigenwerte übersetzt. Dann werden die Reglerparameter so bestimmt, dass die Eigenwerte des Regelkreises durch eine statische Rückführung die gewünschten Werte annehmen. Für Eingrößensysteme existieren unter üblicherweise vorhandenen Voraussetzungen (Steuerbarkeit) eindeutige Lösungen. Für ein Mehrgrößensysteme existieren üblicherweise unendlich viele Lösungen.[9] Verfahren wie Modale Regelung[10] oder die Entkopplung nach Falb-Wolowich[11] schaffen Zusatzbedingungen, so dass wieder eindeutige Lösungen angegeben werden können. Falls die Strecke nicht steuerbar ist, gibt es einzelne feste Eigenwerte, die nicht verändert werden können.
Die Zustandsrückführung erfordert die Kenntnis des Zustandes zu jedem Zeitpunkt. Unter bestimmten Voraussetzungen kann eine Zustandsrückführung durch eine Ausgangsrückführung ersetzt werden, ohne die Lage der erreichten Eigenwerte zu verändern. Ist die Regelstrecke beobachtbar, so kann der Zustandsvektor durch Einsatz eines Beobachters aus den Ausgangsgrößen rekonstruiert werden. Das Separationstheorem sichert dabei, dass (bei korrekter Streckenbeschreibung) Beobachterpole zu den Reglerpolen hinzutreten, diese aber nicht verschieben. Damit ist ein entkoppelter Entwurf von Regler und Beobachter möglich.
In der robusten Regelung steht die Tatsache im Vordergrund, dass das mathematische Modell der Regelstrecke nur eine vereinfachte Näherung der realen Regelstrecke ist. In der robusten Regelung werden Regelungsverfahren entwickelt, die trotz Modellunsicherheiten die Stabilität (robuste Stabilität) bzw. eine Mindestgüte garantieren. Die Garantie gilt unter der Voraussetzung, dass der Modellfehler innerhalb einer analytischen Grenze bleibt.
Zeitdiskrete Regelung
In der zeitdiskreten Regelung, auch digitale Regelung oder Abtastregelung genannt, werden die Regelgröße und die Sollgröße in festen, gleichmäßigen Zeitabständen abgetastet und in digitale Zahlenwerte umgewandelt, also quantisiert. Der Regler berechnet aus diesen quantisierten Größen in jedem Zeitschritt die Stellgröße, die zum Abtastzeitpunkt ausgegeben und in ein Analogsignal umgewandelt wird. Ein Halteglied sichert, dass der Stellwert während des gesamten Zeitintervalls bis zum nächsten Abtastschritt anliegt. Die Quantisierung der Größen führt außerdem auf ein wertediskretes Signal. In der Regel wird die Quantisierung jedoch so fein gewählt, dass die Auswirkungen auf die Kreisdynamik vernachlässigt werden können.
Eine Vorgehensweise zum Entwurf zeitdiskreter Regler ist der Entwurf eines zeitkontinuierlichen Reglers und seiner Approximation durch einen zeitdiskreten Regler. Als Kriterium zur Approximation kann der Differentialquotient, das Integral oder das Pol/Nullstellen-Bild dienen. Diese Herangehensweise funktioniert besonders gut bei starker Überabtastung der Regelstrecke (z. B. das 20-fache der Grenzfrequenz).
Die meisten Prinzipien und Entwurfsverfahren der zeitkontinuierlichen Regelung haben eine sinngemäße Entsprechung in der zeitdiskreten Regelung. Zur mathematischen Behandlung von Abtastregelungen im Frequenzbereich wird dabei die z-Transformation eingesetzt.
Das Wurzelortskurvenverfahren hat eine direkte Entsprechung im zeitdiskreten Bereich, ebenso der Optimalreglerentwurf (LQ-Regler).
Zur Polzuweisung für zeitkontinuierliche Systeme existiert ein sinngemäßes Verfahren für zeitdiskrete Systeme.
Eine Besonderheit ist der Regler mit endlicher Einstellzeit, der es ermöglicht, den Sollwert nach einer endlichen Zahl n von Zeitschritten zu erreichen. Dabei ist n die dynamische Ordnung der Regelstrecke. Dieses verblüffende Ergebnis ist mathematisch durch das Cayley-Hamilton Theorem begründet.
Nichtlinearer Reglerentwurf
Die Methode der harmonischen Balance ist eine Methode zur Analyse nichtlinearer Regelkreise. Sie nutzt eine Beschreibung der nichtlinearen offenen Kette im Frequenzbereich, die auf der Beschreibungsfunktion der offenen Kette beruht. Dabei wird angenommen, dass die nichtlineare offene Kette aus der Reihenschaltung eines linearen und eines nichtlinearen Systems besteht. Die Beschreibungsfunktion hat eine zum Frequenzgang linearer Systeme analoge Bedeutung. Sie gibt an, wie harmonische Schwingungen übertragen werden. Auf Basis dieser Beschreibungsform kann ein Reglerentwurf[12] durchgeführt werden, obwohl die Methode der harmonischen Balance keine Synthesemethode ist.
Die Methode der globalen Linearisierung[13] (auch differentialgeometrische Methode oder exakte Linearisierung genannt) basiert auf der Idee, die Nichtlinearität in der Regelstrecke durch geeignete Vorfilter und Rückführungen zu kompensieren. Anschließend wird für das linearisierte System anhand linearer Reglerentwurfsmethoden das dynamische Verhalten an die Güteforderungen angepasst. Der nichtlineare Entwurf wird somit auf linearen Entwurf zurückgeführt.
Die Flachheitsbasierte Regelung stützt sich auf den Begriff der Flachheit (engl. flatness), der eine Erweiterung des Begriffs der Steuerbarkeit für nichtlineare Systeme ist. Er erlaubt den systematischen Entwurf von Vorsteuerungen für flache nichtlineare Systeme durch Systeminversion. Meist wird die Steuerung durch eine Regelung zur Störunterdrückung ergänzt.Die Idee des Gain scheduling basiert auf der Annahme, dass das nichtlineare System in jedem Betriebspunkt linearisiert werden kann. Für jeden Betriebspunkt wird ein Regler fester Struktur entworfen, dessen Parameter vom Betriebspunkt abhängen. Bei der Realisierung werden die Parameter in Abhängigkeit vom Betriebspunkt eingestellt. Eine spezielle Klasse nichtlinearer System, sind lineare Systeme, deren Systemmatrizen explizit von Parametern θ abhängen. Diese Systeme werden als linear parameter-varying (LPV) Systeme bezeichnet. Im LPV-gain scheduling werden die Reglerparameter explizit von θ abhängig gemacht.
Ein nichtlineares Regelungsverfahren, das mit schaltenden Reglern arbeitet, ist Sliding mode control.
Weitergehende Regelungskonzepte
In zahlreichen Anwendungsgebieten (z. B. Flugregelung) bleibt die Struktur des Modells über den gesamten Arbeitsbereich gültig, es ändern sich jedoch einzelne Parameter. Beispiele sind die Änderung der Dichte von Luft mit der Flughöhe, oder die Masse eines Flugzeuges mit der Zeit. In der adaptiven Regelung werden die Reglerparameter automatisch den sich ändernden Bedingungen angepasst. Für eine allgemeine Übersicht zum Begriff der Adaption siehe Adaption. Kleinere Abweichungen der Regelstrecke vom Entwurfsmodell werden mittels Methoden zur Robusten Regelung abgedeckt.
Die prädiktive Regelung beinhaltet eine spezielle Komponente (den Prädiktor) zur Vorhersage des künftigen Systemverhaltens. Die Vorhersage ermöglicht eine verbesserte Ermittlung des Stellwertes in Bezug auf das gewünschte künftige Verhalten. Klassische Regler ohne Prädiktor müssen die Reaktion der Regelstrecke auf den Stellwert abwarten, können also nur reagieren. Die Prädiktive Regelung bezeichnet diesen allgemeinen Ansatz, wobei unterschiedliche spezifische Realisierungen existieren (Smith-Prädiktor, Internal Model Control, Model Predictive Control). Prädiktive Regelungsstrukturen sind besonders vorteilhaft, wenn die Strecke stark verzögerndes Verhalten aufweist, etwa große Totzeiten.
In der Fuzzy Regelung werden den Signalen (Regelgröße, Regelfehler, Stellwert) symbolische Werte anstatt numerischer Werte zugewiesen[14]. Dieses Vorgehen ist besonders vorteilhaft, wenn intuitives Expertenwissen über die manuelle Regelung des Prozesses vorhanden ist, ein formaler Reglerentwurf wegen eines fehlenden Modells jedoch nicht praktikabel ist. Die Fuzzy Regelung basiert auf der Fuzzy-Logik, die eine Erweiterung der booleschen Logik ist. Die Fuzzy Regelung wurde erstmals zur Steuerung der U-Bahn in Sendai in der Praxis erfolgreich eingesetzt (siehe U-Bahn Sendai).
Neuronale Netze werden in der Regelungstechnik sowohl zur Darstellung von Kennfeld-Reglern als auch zur Systemidentifikation verwendet[15]. Beispielsweise können neuronale Netze zum Autotuning von PID-Reglern oder für die adaptive Regelung eingesetzt werden.
Realisierung von Regelungen
- Hauptartikel: Regler
Regler im Produktionseinsatz
Zur Realisierung eines Regelkreises muss der entworfene Regler physikalisch realisiert werden. Hierzu können Analogrechner, digitale Kompaktregler oder Soft-Regler in einer geeigneten Speicherprogrammierbaren Steuerung eingesetzt werden. Siehe auch Artikel Regler, sowie[16][17][18].
Je nach Aufbau und Einsatzzweck lassen sich unterscheiden:
- Industrieregler → maschinennahe Einzelregler für Kleinanlagen mit eigenem Mikroprozessor
- Prozessregelgeräte → erweiterbare Industrieregler mit Schnittstelle zu übergelagertem (Leit-)System
- Universalregler → Prozessregler in Form von Erweiterungskarten oder Software-Regelbausteinen für programmierbare Steuerungen
- Branchenregler → Spezielle Prozessregler, die für bestimmte Anwendungsgebiete optimiert sind.
Rapid-Prototyping in Forschung und Entwicklung
In der Forschung und Entwicklung entsteht regelmäßig das Problem, neue Regelungskonzepte zu testen. Die wichtigsten Software-Werkzeuge für rechnergestützte Analyse, Entwurf und Rapid Control Prototyping von Regelungen sind nachfolgend aufgeführt.
- MATLAB und Simulink, The MathWorks: Durch zahlreiche Toolboxes ein sehr umfangreiches Softwarepaket für numerische Mathematik, für Simulation, Systemidentifikation, Reglerentwurf und Rapid Control Prototyping geeignet (kommerziell)
- Scilab, Institut National de Recherche en Informatique et en Automatique (INRIA): Ebenfalls sehr umfangreiches Softwarepaket für numerische Mathematik mit ähnlichem Konzept und ähnlicher Syntax wie MATLAB, für Simulation, Systemidentifikation und Rapid Control Prototyping geeignet (frei)
- CAMeL-View TestRig: Entwicklungsumgebung zur Modellbildung von physikalischen Systemen mit dem Schwerpunkt Reglerentwurf und Rapid Control Prototyping sowie zur Anbindung an Versuchsstände (kommerziell)
- Maple: Computeralgebra-System, beherrscht numerische und symbolische Mathematik, besonders für manche Entwurfsverfahren der nichtlinearen Regelung geeignet (kommerziell)
- Mathematica, Wolfram Research, Inc.: Umfangreiches Softwarepaket für numerische und symbolische Mathematik (kommerziell)
- dSPACE: Integrierte Hard- und Software-Lösungen für die Anbindung von MATLAB an Versuchsstände (kommerziell)
- LabVIEW, National Instruments (NI): Integrierte Hard- und Software-Lösungen für die Rechnersteuerung von Versuchsständen (kommerziell)
Alle aufgeführten Werkzeuge zeigen ein hohes Maß an Flexibilität bezüglich der Anwendung und der verwendbaren Reglerstrukturen.
Anwendungen und Beispiele
Häufige Regelungsprobleme
Nachfolgende Auflistung nennt unabhängig von konkreten Anwendungen einige physikalische bzw. chemische Größen, die typischerweise als Regelgrößen auftreten. Auf konkrete Anwendungen wird im nächsten Abschnitt eingegangen.
- Temperaturregelung
- Druck- und Kraftregelung
- Durchfluss- und Mengenregelung
- Füllstandsregelung
- Lage-, Positions-, und Entfernungsregelung
- Geschwindigkeits- und Beschleunigungsregelung
- Drehzahl- und Drehmomentregelung
- Regelung chemischer Größen, wie Konzentrationen, in der Verfahrenstechnik
Technische Anwendungen
- Bahntechnik: In der Antriebsregelung treten vielfältige Regelungsprobleme auf, es sind beispielsweise Drehmoment und Geschwindigkeit zu regeln. An der U-Bahn Sendai wurde die Fuzzy-Regelung erfolgreich eingesetzt.
- Luftfahrt: Regelungsprobleme treten in zahlreichen Komponenten von Flugzeugen auf, etwa in den Turbinen, aber auch bezogen auf die Flugdynamik. Beispiele für flugdynamische Regelungsprobleme sind die Kontrolle der Roll-, Gier-, und Nickwinkel, sowie der Autopilot. Siehe auch Flugsteuerung.
- Energietechnik: Stellungsregelung eines Stellventils mit Stellantrieb innerhalb einer Reglerkaskade. In Elektroenergienetzen sind Spannung und Frequenz netzweit zu halten. In jedem Kraftwerk werden Spannung und Frequenz lokal geregelt, so dass die Aufgabe mit dezentralen Reglern durch Variation der Regelleistung gelöst wird (siehe auch Kraftwerksmanagement). Global werden lediglich die Leistungssollwerte der einzelnen Kraftwerke vorgegeben. Die Drehzahlregelung einer Dampfmaschine mit Fliehkraftregelung ist ein klassischer Anwendungsfall
- Kraftfahrzeugtechnik: Tempomat und Antiblockiersystem (ABS), aber auch elektronisches Stabilitätsprogramm sind bekannte Regelungen im Fahrzeugbereich, die auch als Fahrerassistenzsysteme bezeichnet werden. Auch Verbrennungsmotoren beinhalten vielfältige Regelkreise, beispielsweise für Leerlaufdrehzahl, Luftverhältnis (siehe auch Lambdasonde), Klopfregelung (siehe auch Klopfen (Verbrennungsmotor)). Moderne automatische Schaltgetriebe benötigen ebenfalls Regelkreise für die Synchronisation beim Schalten.
- Pipeline: In Pipelines kommen vor allem vermaschte Regelungen vor, für Durchfluss, Druckregelung (Vordruck, Nachdruck) und Stellungsregelung einschließlich Grenzwertregelung.
- Robotik: In der Fertigungsautomatisierung sind die Achsen der Fertigungsroboter zu positionieren. Hier spielen eine schnelle Beruhigungszeit und geringstes Überschwingen eine besonders große Rolle.
- Verfahrenstechnik: In verfahrenstechnischen Prozessen treten Regelungsprobleme für jegliche chemische und physikalische Größen auf, die im betrachteten Prozess eine Rolle spielen. Beispiele sind die Regelung von Füllstand, Temperatur, pH-Wert und Sauerstoffgehalt eines Rührkessel-Reaktors oder das konstant halten von Stoff- bzw. Ionenkonzentrationen mit einem Chemostaten.
- Wasserwirtschaft: Zur Vermeidung von Überschwemmungen und Sicherung der Wasserversorgung sind unterlagerte Regelungen von Ketten von Talsperren bedeutsam. Der Füllstand eines einzelnen Stausees wird von einem übergeordneten Management vorgegeben und lokal geregelt.
Geschichte
Die Regelungstechnik hat eine faszinierende Geschichte durchgemacht[19]. Erste Regler wurden bereits ab 300 v.Chr. im alten Griechenland entwickelt. So wurde die Wasseruhr des griechischen Ingenieurs Ktesibios aus Alexandria (Ägypten) durch einen Schwimmer geregelt. Philon von Byzanz erfand 250 v.Chr. eine Öllampe, bei der ein Schwimmer den Ölstand regulierte. Bei den ersten rückgekoppelten Systemen handelte es sich ausschließlich um Wasserstandsregulierungen. Der erste Temperaturregler in Form eines rückgekoppelten Systems erfand der Niederländer Cornelis Jacobszoon Drebbel. Denis Papin aus Frankreich erfand 1681 den ersten Druckregulator für einen Dampfkessel.
Der erste industrielle Regler mit einem Rückkoppelungsmechanismus wird dem Erfinder James Watt mit seinem Fliehkraftregler zugeschrieben, den er 1769 für die von Thomas Newcomen erfundene Dampfmaschine entwickelt hat. Zeitgleich erfand der Russe Ivan Polzunov mit seinem Wasserstandsregler ebenfalls das erste rückgekoppelte System der Geschichte. Dabei nimmt ein Schwimmer den aktuellen Wert des Wasserstands auf und überträgt den Wert über ein Gestänge an das Einlassventil des Dampfkessels. Ab 1868 wurde die Regelungstechnik durch immer bessere Erfindungen stark vorangetrieben. Als es darum ging, die Genauigkeit der Regelungssysteme zu erhöhen, wurde erkannt, dass eine umfassende Theorie auf dem Gebiet der Regelungstechnik entwickelt werden musste. Eine erste mathematische Theorie wurde von James Clerk Maxwell aufgestellt, bei der Maxwell ein mathematisches Modell mit Differentialgleichungen für den Fliehkraftregler aufstellte[20].
Bis zum 2. Weltkrieg entwickelten sich Theorie und Praxis der Regelungssysteme in den USA und Westeuropa anders als in Russland und Osteuropa. Während im Westen die Entwicklung der Theorie rückgekoppelter Systeme vorwiegend im Frequenzbereich, vor allem von Hendrik Wade Bode, Harry Nyquist und Harold Stephen Black, vorangetrieben wurde, lösten die Mathematiker und Mechaniker in der ehemaligen UdSSR um Vyschnegradsky und in Europa um Barkhausen, die Probleme vorwiegend im Zeitbereich unter Anwendung von Differentialgleichungen.
Der große Durchbruch der Regelungstechnik fand mit dem 2. Weltkrieg statt, da man sich im Rahmen der militärischen Aufrüstung mit der Entwicklung von komplexen militärischen Systemen befassen musste. Radarsysteme, Autopiloten und automatische Zieleinrichtungssysteme sind nur einige Beispiele, welche alle auf rückgekoppelten Systemen beruhen. Der Bedarf an neuen Regelungssystemen führte in der Theorie und Praxis zur Erforschung und Verbesserung neuer mathematischer Methoden und Verfahren, welche die Regelungstechnik zu einer eigenständigen Disziplin entwickelten. Die Gründung der International Federation of Automatic Control (IFAC) im September 1956 fällt zeitlich mit dem Ursprung der sogenannten modernen Regelungstheorie zusammen, zu deren Entwicklung Rudolf Kálmán maßgeblich beitrug. In den 80er Jahren erfuhr die Regelungstechnik mit der Einführung des digitalen Rechners einen erneuten Entwicklungsschub. Dieses neue Werkzeug ermöglichte den Regelungstechnikern ihre Berechnungen schneller und genauer auszuführen, was zur Entwicklung von komplexen und hochpräzisen Steuerungssystemen führte.
Berufsverbände mit Bezug zur Regelungstechnik
Deutschland
International
- International Federation of Automatic Control (IFAC)
- Institute of Electrical and Electronics Engineers (IEEE)
Siehe auch
Portal: Mess-, Steuerungs- und Regelungstechnik – Übersicht zu Wikipedia-Inhalten zum Thema Mess-, Steuerungs- und RegelungstechnikLiteratur
- Otto Föllinger: Regelungstechnik. Hüthig Verlag, ISBN 3-7785-2336-8.
- Martin Horn, Nicolaos Dourdoumas: Regelungstechnik. Pearson Studium, 2006, ISBN 3-8273-7260-7.
- Rolf Isermann: Identifikation dynamischer Systeme. Band 1 und 2, Springer Verlag, 1992, ISBN 3-540-55468-8.
- Lennart Ljung: System Identification - Theory for the User. Prentice Hall, ISBN 0-13-656695-2.
- Jan Lunze: Regelungstechnik 1. 6 Auflage. Springer Verlag, Berlin 2007, ISBN 978-3-540-70790-5. Regelungstechnik 2. 4 Auflage. Springer Verlag, Berlin 2006, ISBN 978-3-540-32335-8.
- Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik. 7. Auflage. Verlag Harry Deutsch, 2007, ISBN 978-3-8171-1807-6.
- Heinz Mann, Horst Schiffelgen, Rainer Froriep,: Einführung in die Regelungstechnik. Carl Hanser Verlag, München 2005, ISBN 3-446-40303-5.
- Kurt Reinschke: Lineare Steuerungs- und Regelungstheorie. Springer Verlag, Dresden 2005, ISBN 3-540-21886-6.
- Gerd Schulz: Regelungstechnik. Oldenbourg Verlag, 2002, ISBN 3-486-25858-3.
- Heinz Unbehauen: Regelungstechnik. 1, Vieweg, Braunschweig 2005, ISBN 3-528-93332-1. Regelungstechnik. 2, Vieweg, Braunschweig 2000, ISBN 3-528-73348-9.
- Josef Uphaus: Regelungstechnik. Bildungsverlag Eins, 2005, ISBN 3-427-44510-0.
- samson.de (Hrsg.): Begriffe und Symbole der Regelungstechnik. (pdf).
Zeitschriften und Journale:
- VDI/VDE-GMA, NAMUR (Interessengemeinschaft Prozessleittechnik der chemischen und pharmazeutischen Industrie) (Hrsg.): at – Automatisierungstechnik. 1953ff (at-technik.de ; monatlich). atp – Automatisierungstechnische Praxis. München, ISSN 0178-2320. atpi – Automation Technology in Practice. Oldenbourg Wissenschaftsverlag (weblink).
- MSR-Magazin. Zeitschrift für Messen, Steuern, Regeln. Verlag für Technik & Wirtschaft VTW (industrie-service.de, VTW).
- International Journal of Control. Taylor & Francis (tandf.co.uk).
- IFAC (Hrsg.): Automatica. Elsevier (elsevier.com).
- European Journal of Control. hermes Science (elet.polimi.it, editions-hermes.fr).
- Institution of Engineering and Technology (IET) (Hrsg.): IEE Proceedings - Control Theory & Applications. (ietdl.org, IET: theiet.org).
- Norwegian Society of Automatic Control (Hrsg.): Modeling, Identification and Control. (itk.ntnu.no, nfaplassen.no).
- Wroclaw University of Technology (Hrsg.): Systems Science. (Wroclaw UT).
- IEEE Control Systems Society (CSS) (Hrsg.): IEEE Control Systems Magazine. (web). IEEE Transactions on Automatic Control. (web). IEEE Transactions on Control Systems Technology. (web, ieeecss.org).
- ASME American Society Of Mechanical Engineers (Hrsg.): Journal of Dynamic Systems, Measurement, and Control. (scitation.aip.org, asme.org).
Weblinks
Deutschland
Einzelnachweise
- ↑ Mann/Schiffelgen/Froriep: Einführung in die Regelungstechnik. Carl Hanser Verlag, München 2005, ISBN 3-446-40303-5
- ↑ a b c d e Jan Lunze: Regelungstechnik 1. Springer Verlag, 2005, ISBN 3-540-28326-9
- ↑ a b c d Heinz Unbehauen: Regelungstechnik 1, Vieweg, Braunschweig/Wiesbaden 2005, ISBN 3-528-93332-1
- ↑ Rolf, Isermann: Identifikation dynamischer Systeme, Band 1. Springer Verlag, 1992, ISBN 3-540-55468-8
- ↑ Lennart Ljung: System Identification, Prentice Hall, 1999, ISBN 0-13-656695-2
- ↑ Oliver Nelles: Nonlinear System Identification. Springer-Verlag, 2001, ISBN 3-540-67369-5
- ↑ Otto Föllinger: Nichtlineare Regelungen II. Oldenbourg Verlag, 1980, ISBN 3-486-33253-8, Kap. 5.2
- ↑ Otto Föllinger: Nichtlineare Regelungen II. Oldenbourg Verlag, 1980, ISBN 3-486-33253-8, Kap. 5.8
- ↑ Otto Föllinger, Regelungstechnik, 8. Aufl. 13.3.3
- ↑ Otto Föllinger, Regelungstechnik, 8. Aufl. 13.3.3
- ↑ Otto Föllinger, Regelungstechnik, 8. Aufl. 13.5
- ↑ Otto Föllinger: Nichtlineare Regelungen II. Oldenbourg Verlag, 1980, ISBN 3-486-33253-8, Kap. 4
- ↑ Otto Föllinger: Nichtlineare Regelungen II. Oldenbourg Verlag, 1980, ISBN 3-486-33253-8, Kap. 7
- ↑ Lefteri H. Tsoukalas, Robert E. Uhrig: Fuzzy and Neural Approaches in Engineering. Wiley-Interscience, 1997, ISBN 0-471-16003-2, Kap. 6
- ↑ Lefteri H. Tsoukalas, Robert E. Uhrig: Fuzzy and Neural Approaches in Engineering. Wiley-Interscience, 1997, ISBN 0-471-16003-2, Kap. 10
- ↑ Jürgen Müller: Regeln mit SIMATIC. Publicis Corporate Publishing, Erlangen 2004, ISBN 3-89578-248-3
- ↑ Manfred Schleicher: Regelungstechnik für den Praktiker. Fa. JUMO GmbH & Co, 2006, ISBN 3-935742-00-2
- ↑ Berthold Heinrich [Hrsg.]: Messen, Steuern, Regeln. Vieweg Verlag, Wiesbaden 2005, ISBN 3-8348-0006-6
- ↑ Special issue on the history of control, IEEE Control Systems Magazine, Vol. 16, June 1996
- ↑ Stuart Bennett: A brief history of automatic control, IEEE Control Systems Magazine, Vol. 16, pp. 17-25, June 1996
Wikimedia Foundation.