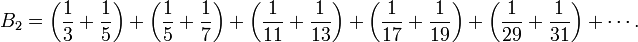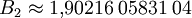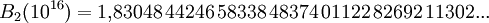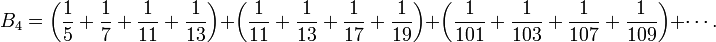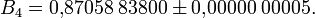Brun'sche Konstante

Im Jahr 1919 zeigte der Mathematiker Viggo Brun (1885–1978), dass die Summe der Kehrwerte von Primzahlzwillingen (Paare von Primzahlen, die sich um die Differenz von 2 unterscheiden) konvergiert. Der Grenzwert dieser Summe wird Brunsche Konstante für Primzahlzwillinge genannt und meist als B₂ bezeichnet:

$B_2 = \left(\frac{1}{3} + \frac{1}{5}\right) + \left(\frac{1}{5} + \frac{1}{7}\right) + \left(\frac{1}{11} + \frac{1}{13}\right) + \left(\frac{1}{17} + \frac{1}{19}\right) + \left(\frac{1}{29} + \frac{1}{31}\right) + \cdots.$

Dieses Ergebnis der analytischen Zahlentheorie ist auf den ersten Blick überraschend, da die Summe der Kehrwerte aller Primzahlen divergiert, wie bereits im 18. Jahrhundert von Leonhard Euler bewiesen wurde. Wäre auch B₂ divergent, hätte man einen Beweis für die bis heute offene Vermutung, dass es unendlich viele Primzahlzwillinge gibt (Alphonse de Polignac (1817-1890), 1849). Aus der Konvergenz lässt sich jedoch nicht auf das Gegenteil schließen.

Die Idee zur Berechnung besteht darin, dass die Summation zunächst möglichst weit durchgeführt wird und dann der fehlende Rest abgeschätzt wird. So haben Daniel C. Shanks (1917−1996) und John William Wrench, jr. (* 1911) alle Primzahlzwillinge unterhalb 2·10⁶ benutzt.

Eine Schätzung

$B_2\approx 1{,}90216\;05831\;04$

stammt von Pascal Sebah aus dem Jahr 2002, der hierfür alle Primzahlzwillinge bis 10¹⁶ betrachtete. Die Berechnung von B₂ ist allerdings außerordentlich schwierig, zum einen, da die Reihe sehr langsam konvergiert, zum anderen, da das Auffinden aller großer Primzahlzwillinge äußerst kompliziert ist (siehe auch: Primzahltests).

1994 entdeckte Thomas R. Nicely bei einer Abschätzung von B₂ über alle Primzahlzwillinge bis 10¹⁴ den sogenannten Pentium-FDIV-Bug. Er gibt am 19. März 2008 die bislang genaueste Abschätzung an:

$B_2 = 1{,}90216\;05831\;05 \pm 0{,}00000\;00011\;25$.

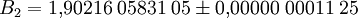Hierfür wurden die Kehrwerte aller 10 304 195 697 298 Primzahlzwillinge unterhalb 10¹⁶ summiert:

$B_2(10^{16}) = 1{,}83048\,44246\,58338\,48374\,01122\,82692\,11302...$ ^[1]

Neben B₂ gibt es noch die brunsche Konstante für Primzahlvierlinge, gewöhnlich als B₄ bezeichnet. Primzahlvierlinge sind Paare von Primzahlzwillingen, die einen Abstand von 4 haben (dies ist der kleinst mögliche Abstand zweier Primzahlzwillinge zueinander). Die ersten drei Quadrupel von Primzahlvierlingen sind (5, 7, 11, 13), (11, 13, 17, 19) und (101, 103, 107, 109).

$B_4 = \left(\frac{1}{5} + \frac{1}{7} + \frac{1}{11} + \frac{1}{13}\right) + \left(\frac{1}{11} + \frac{1}{13} + \frac{1}{17} + \frac{1}{19}\right) + \left(\frac{1}{101} + \frac{1}{103} + \frac{1}{107} + \frac{1}{109}\right) + \cdots.$

Da alle Summanden von B₄ auch in B₂ vorkommen – bis auf die Summanden aus dem ersten Vierling sind keine Werte doppelt vorhanden – und der Summand 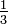$\tfrac 13$ in B₄ nicht auftritt, gilt 0 < B₄ < B₂, und somit konvergiert auch diese Reihe. Sie hat den Wert

$B_4 = 0{,}87058\; 83800 \pm 0{,}00000\; 00005.$

Einzelnachweise

1. ↑ Thomas R. Nicely: Prime Constellations Research Project (11.12.08)

Weblinks

• Eric W. Weisstein: Brunsche Konstante auf MathWorld (englisch)
• Thomas R. Nicely: Prime Constellations Research Project