Goldbachsche Vermutung

Die Goldbachsche Vermutung, benannt nach dem Mathematiker Christian Goldbach, ist eine unbewiesene Aussage aus dem Bereich der Zahlentheorie.

Starke (oder binäre) Goldbachsche Vermutung

Die starke (oder binäre) Goldbachsche Vermutung lautet wie folgt:

Jede gerade Zahl größer als 2 kann als Summe zweier Primzahlen geschrieben werden.

Mit dieser Vermutung befassten sich bis in die heutige Zeit viele Zahlentheoretiker, ohne sie beweisen oder widerlegen zu können.

Tomás Oliveira e Silva zeigte mittels eines Verteiltes-Rechnen-Projekts mittlerweile (Stand November 2010) die Gültigkeit der Vermutung für alle Zahlen bis 2 × 10¹⁸. Ein Beweis dafür, dass sie für jede beliebig große gerade Zahl gilt, ist dies natürlich nicht.

Nachdem der britische Verlag Faber & Faber im Jahr 2000 ein Preisgeld von einer Million Dollar auf den Beweis der Vermutung ausgelobt hatte, wuchs auch das öffentliche Interesse an dieser Frage. Das Preisgeld wurde nicht ausgezahlt, da bis April 2002 kein Beweis eingegangen war.

Brief von Goldbach an Euler vom 7. Juni 1742 (lateinisch-deutsch)^[1]

Schwache (oder ternäre) Goldbachsche Vermutung

Die von Christian Goldbach ursprünglich geäußerte Vermutung war schwächer. Er formulierte sie erstmals in einem Brief an Leonhard Euler 1742 wie folgt:

Jede ungerade Zahl größer als 5 kann als Summe dreier Primzahlen geschrieben werden.

In dieser Form ist die Goldbachsche Vermutung eines der ältesten Probleme der Zahlentheorie (siehe ungelöste Probleme der Mathematik).

Heute ist diese Vermutung als ternäre oder schwache Goldbachsche Vermutung bekannt. Sie ist teilweise gelöst: Denn einerseits gilt sie, wenn die verallgemeinerte Riemannsche Vermutung richtig ist,^[2] und andererseits ist gezeigt, dass sie für genügend große Zahlen gilt (Satz von Winogradow, siehe Verwandte Resultate).

Aus der starken Goldbachschen Vermutung folgt die schwache Goldbachsche Vermutung, denn jede ungerade Zahl u kann als Summe u = (u − 3) + 3 geschrieben werden. Der erste Summand (u − 3) kann nach der starken Goldbachschen Vermutung als Summe zweier Primzahlen (a und b) geschrieben werden, womit eine Zerlegung von u in drei Primzahlen (a, b und 3) gefunden ist.

Goldbach-Zerlegungen

Anzahl der Möglichkeiten, die geraden Zahlen bis 200000 als Summe zweier Primzahlen zu schreiben

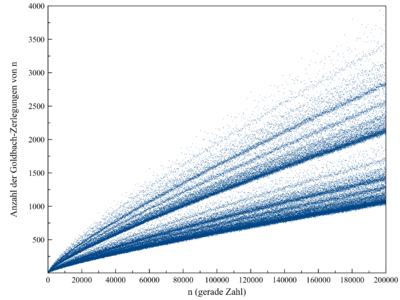
Als Goldbach-Zerlegung wird die Darstellung einer geraden Zahl als Summe zweier Primzahlen bezeichnet, beispielsweise ist 3 + 5 eine Goldbach-Zerlegung der 8. Die Zerlegungen sind nicht eindeutig, wie man an 18 = 7 + 11 = 5 + 13 ersehen kann. Für größere gerade Zahlen gibt es eine tendenziell wachsende Anzahl von Goldbach-Zerlegungen („mehrfache Goldbachzahlen“). Die Anzahl der Goldbach-Zerlegungen lässt sich mit Computerunterstützung leicht berechnen, siehe Abbildung.

Um die starke Goldbachsche Vermutung zu verletzen, müsste ein Datenpunkt irgendwann auf die Nulllinie fallen.

Die Forderung an eine gerade Zahl n, dass für jede Primzahl p mit $n/2 \leq p < n$ auch n − p eine Primzahl und somit n = p + (n − p) eine Goldbach-Zerlegung ist (die Zahl n also die maximale Anzahl an Goldbach-Zerlegungen besitzt), erfüllen genau die vier Zahlen 10, 16, 36 und 210. Auch die schwächere Forderung, dass für jede Primzahl p mit $n/2 \leq p < n-1$ auch n − p eine Primzahl ist, erfüllt keine Zahl n > 210.^[3]

Verwandte Resultate

• Bewiesen ist inzwischen, dass jede gerade Zahl (größer als 2) als Summe von höchstens sechs Primzahlen ausgedrückt werden kann.^[4]
• 1920 bewies Viggo Brun, dass jede genügend große gerade Zahl als Summe zweier Zahlen mit maximal 9 Primfaktoren darstellbar ist.
• 1937 bewies Winogradow, dass jede genügend große ungerade Zahl als Summe dreier Primzahlen geschrieben werden kann (schwache Goldbachsche Vermutung für den Spezialfall genügend großer Zahlen).
• 1938 bewies Nikolai Grigorjewitsch Tschudakow, dass "fast alle" geraden Zahlen als Summe zweier Primzahlen darstellbar sind.
• 1947 bewies Alfred Renyi, dass eine Konstante K derart existiert, dass jede gerade Zahl als Summe einer Primzahl und einer Zahl mit maximal K Primfaktoren geschrieben werden kann.
• 1966 bewies der Mathematiker Chen, dass jede hinreichend große gerade Zahl als Summe einer Primzahl und einer Zahl geschrieben werden kann, die höchstens zwei Primfaktoren besitzt.^[5]

Siehe auch

• Hilberts 23 Probleme

Literatur

• Wolfgang Blum: Goldbach und die Zwillinge. Spektrum der Wissenschaft Dossier 6/2009: „Die größten Rätsel der Mathematik“, ISBN 978-3-941205-34-5, S. 34–39.
• Apostolos Doxiadis: Onkel Petros und die Goldbach’sche Vermutung. Lübbe, 2000, ISBN 3-7857-0951-X (Belletristik)
• Andrew Granville: Refinements of Goldbach’s conjecture, and the generalized Riemann hypothesis (PDF-Datei, 180 kB), Functiones et Approximatio 37, 2007, S. 7–21 (englisch)
• Melvyn B. Nathanson: Additive Number Theory. The Classical Bases, Springer-Verlag, New York 1996 (englisch)
• Jörg Richstein: Verifying the Goldbach conjecture up to 4·10¹⁴, Mathematics of Computation 70, 2001, S. 1745–1749 (englisch)

Weblinks

• Goldbach conjecture verification project von Tomás Oliveira e Silva

Einzelnachweise

1. ↑ in Druckschrift in Paul Heinrich Fuss (Hrsg.): Correspondance mathématique et physique de quelques célèbres géomètres du XVIIIème siècle (Band 1), St.-Pétersbourg 1843, S. 125–129
2. ↑ Jean-Marc Deshouillers, Gove Effinger, Herman te Riele, Dmitrii Zinoviev: A complete Vinogradov 3-primes theorem under the Riemann hypothesis, Electronic Research Announcements of the AMS 3, 1997, S. 99–104 (englisch)
3. ↑ Jean-Marc Deshouillers, Andrew Granville, Władysław Narkiewicz, Carl Pomerance: An upper bound in Goldbach’s problem, Mathematics of Computation 61 Nr. 203, Juli 1993, S. 209–213 (englisch)
4. ↑ Olivier Ramaré: On Šnirel’man’s constant. Annali della Scuola Normale Superiore di Pisa 22, 1995, S. 645–706 (englisch)
5. ↑ Sci. Sinica Band 16, 1973, S. 157