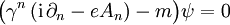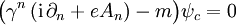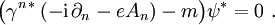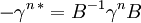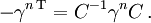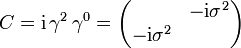C-Parität

Die Ladungskonjugation oder C-Parität (für englisch Charge = Ladung) ersetzt in quantenmechanischen Zuständen jedes Teilchen durch sein Antiteilchen. Sie spiegelt so das Vorzeichen der Ladung und lässt Energie, Impuls, Masse und Spin jedes Teilchens unverändert.

Die elektromagnetischen und die starken Wechselwirkungen sind invariant unter Ladungskonjugation (kurz C-invariant), das heißt, bei Streuung oder Zerfall verhalten sich die ladungsgespiegelten Zustände so wie die ursprünglichen Zustände. Die Schwache Wechselwirkung ist nicht C-invariant: Der Anteil des Elektrons, der bei schwachen Wechselwirkungen in ein Elektronneutrino und ein W ⁻ -Boson übergehen kann, wird bei Ladungskonjugation durch den Teil des Positrons ersetzt, der nicht an die W-Bosonen koppelt.

Ladungskonjugation des Dirac-Feldes

Das Dirac-Feld ψ wird bei Ladungskonjugation auf das Feld ψ_c transformiert, das mit umgekehrter Ladung e an die elektromagnetischen Potentiale A₀,A₁,A₂,A₃ koppelt. Wenn ψ die Dirac-Gleichung (über den doppelten Index n ist zu summieren)

$\bigl( \gamma^n\,(\mathrm i\,\partial_n -e A_n) - m\bigr)\psi=0$

erfüllt, dann soll das ladungskonjugierte Feld ψ_c der Gleichung

$\bigl( \gamma^n\,(\mathrm i\,\partial_n +e A_n) - m\bigr)\psi_c=0$

genügen.

Komplex Konjugieren der ersten Gleichung ergibt

$\bigl(\gamma^{n\,*}\,(-\mathrm i\,\partial_n -e A_n) - m\bigr)\psi^*=0\ .$

Es erfüllt also ψ_c = Bψ ^* die ladungskonjugierte Gleichung, wenn B eine Matrix ist, für die

$-\gamma^{n\,*}=B^{-1} \gamma^n B$

gilt. Solch eine Matrix gibt es für jede Darstellung der Dirac-Matrizen, denn alle irreduziblen Darstellungen der Dirac-Algebra sind einander äquivalent, und 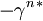$-\gamma^{n\,*}$ stellt die Dirac-Algebra ebenso dar wie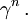 $\gamma^{n}\,.$

Schreibt man 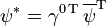$\psi^*=\gamma^{0\,\text{T}}\,\overline{\psi}^{\text{T}}$, so hat das ladungskonjugierte Feld die Form

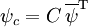$\psi_c = C \,\overline{\psi}^{\text{T}}$ mit der Ladungskonjugationsmatrix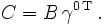 $C=B\,\gamma^{0\,\text{T}}\,.$

Wegen 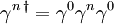$\gamma^{n\,\dagger}=\gamma^0 \gamma^n \gamma^0$ erfüllt die Ladungskonjugationsmatrix

$-\gamma^{n\,\text{T}}=C^{-1} \gamma^n C\,.$

In der Dirac-Darstellung der Gamma-Matrizen kann die Ladungskonjugationsmatrix als

$C = \mathrm i\, \gamma^2\,\gamma^0= \begin{pmatrix} & -\mathrm i \sigma^2\\ -\mathrm i\sigma^ 2 \end{pmatrix}$

so gewählt werden, dass sie reell, antisymmetrisch und unitär ist, $-C = C^ {-1}=C^ {\text{T}}=C^\dagger\,.$

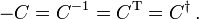
Literatur

• Claude Itzykson, Jean-Bernard Zuber: Quantum Field Theory. McGraw-Hill, New York 1980, ISBN 0-07-032071-3.

Siehe auch

• Paritätsverletzung
• CP-Verletzung
• CPT-Theorem