Co-Graph

In der Informatik ist ein Co-Graph ein ungerichteter Graph  $G = (V, E)\,$ , welcher sich mit bestimmten elementaren Operationen konstruieren lässt. Auf Co-Graphen lassen sich viele schwere Probleme wie z. B. UNABHÄNGIGE MENGE, CLIQUE und KNOTENÜBERDECKUNG in Linearzeit lösen.

Definition

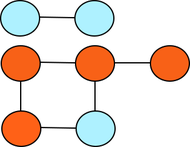
Abbildung eines Co-Graphen. Wie man sieht, ist kein induzierter  $P_{4}\,$  enthalten.

Dieser Graph ist kein Co-Graph, da ein induzierter  $P_{4}\,$  enthalten ist.

Ein Graph  $G = (V, E)\,$  ist ein Co-Graph, falls er sich mit den folgenden drei Operationen konstruieren lässt:

1. Der Graph  $K_{1}\,$  mit genau einem Knoten ist ein Co-Graph ( in Zeichen  $K_{1} = \bullet\,$ ).
2. Für zwei Co-Graphen  $G_{1} = (V_{1}, E_{1})\,$  und  $G_{2} = (V_{2}, E_{2})\,$  ist die disjunkte Vereinigung  $G_{1} \cup G_{2} := (V_{1} \cup V_{2}, E_{1} \cup E_{2})$  ein Co-Graph.
3. Für zwei Co-Graphen  $G_{1} = (V_{1}, E_{1})\,$  und  $G_{2} = (V_{2}, E_{2})\,$  ist die disjunkte Summe  $G_{1} \times G_{2} := (V_{1} \cup V_{2}, E_{1} \cup E_{2} \cup \lbrace \lbrace u, v \rbrace | u \in V_{1}, v \in V_{2} \rbrace)$  ein Co-Graph.

Äquivalente Charakterisierungen

Für einen Graphen  $G\,$  sind folgende Aussagen äquivalent:

•  $G\,$  ist ein Co-Graph.
•  $G\,$  enthält keinen induzierten  $P_{4}\,$ , wobei  $P_{4}\,$  den ungerichteten Weg mit vier Knoten bezeichnet.
• Der Komplementgraph jedes zusammenhängenden induzierten Teilgraphen von  $G\,$  mit mindestens zwei Knoten ist unzusammenhängend.
•  $G\,$  lässt sich mit den folgenden drei Regeln konstruieren:

1. Jeder Graph  $K_{1}\,$  mit genau einem Knoten ist ein Co-Graph.
2. Für zwei Co-Graphen  $G_{1}\,$  und  $G_{2}\,$  ist die disjunkte Vereinigung  $G_{1} \cup G_{2}$  ein Co-Graph.
3. Für einen Co-Graphen  $G\,$  ist auch der Komplementgraph  $\bar G$  ein Co-Graph.

Co-Baum

Um auf Co-Graphen effizient schwere Probleme lösen zu können, kann man sie mithilfe von Co-Bäumen darstellen. Ein Co-Baum ist ein binärer Baum, dessen Blätter mit  $\bullet\,$  und dessen innere Knoten mit  $\cup\,$  bzw.  $\times\,$  markiert sind.

Ein Co-Baum  $T\,$  ist wie folgt definiert:

1. Der Co-Baum  $T\,$  zu dem Co-Graphen  $G = \bullet\,$  ist der Baum mit einem Knoten, der mit  $\bullet\,$  markiert ist.
2. Seien  $G_{1}\,$  und  $G_{2}\,$  Co-Graphen mit den Co-Bäumen  $T_{1}\,$  und  $T_{2}\,$ . Der Co-Baum  $T\,$  zu der disjunkten Vereinigung von  $G_{1}\,$  und  $G_{2}\,$  besteht aus einem mit  $\cup\,$  markierten Wurzelknoten mit den Kindern  $T_{1}\,$  und  $T_{2}\,$ .
3. Seien  $G_{1}\,$  und  $G_{2}\,$  Co-Graphen mit den Co-Bäumen  $T_{1}\,$  und  $T_{2}\,$ . Der Co-Baum  $T\,$  zu der disjunkten Summe von  $G_{1}\,$  und  $G_{2}\,$  besteht aus einem mit  $\times\,$  markierten Wurzelknoten mit den Kindern  $T_{1}\,$  und  $T_{2}\,$ .

Beispiel

Das nachfolgende Beispiel skizziert die Konstruktion eines Co-Graphen  $G_{5}\,$  mit zugehörigem Co-Baum  $T_{5}\,$ :

Co-Graph	Darstellung des Co-Graphen	Darstellung des Co-Baumes	Co-Baum
$G_{1} = \bullet\,$			$T_{1}\,$
$G_{2} = G_{1} \cup G_{1}\,$			$T_{2}\,$
$G_{3} = G_{1} \times G_{2}\,$			$T_{3}\,$
$G_{4} = G_{3} \cup G_{3}\,$			$T_{4}\,$
$G_{5} = G_{1} \times G_{4}\,$			$T_{5}\,$

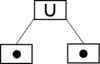
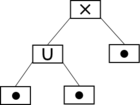
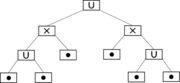
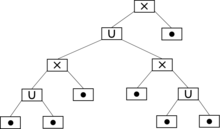
Weitere Beispiele für Co-Graphen sind vollständige Graphen und vollständig unzusammenhängende Graphen.

Eigenschaften von Co-Graphen

Es ist leicht einzusehen, dass Co-Graphen unter Komplementbildung abgeschlossen sind. Um den Komplementgraphen zu erzeugen, müssen im zugehörigen Co-Baum lediglich die Operationen  $\cup\,$  und  $\times\,$  vertauscht werden.

Weiterhin sind ist die Menge der Co-Graphen unter Bildung induzierter Teilgraphen abgeschlossen.

Ebenfalls ist bekannt, dass jeder Co-Graph ein perfekter Graph ist.

Anwendung in der Algorithmik

Einige schwere Graphenprobleme lassen sich auf Co-Graphen in Linearzeit lösen. Dazu zählen u. A. die Probleme UNABHÄNGIGE MENGE, CLIQUE und KNOTENÜBERDECKUNG.

Mithilfe von dynamischer Programmierung auf den zugehörigen Co-Bäumen lassen sich einfach und elegant Lösungen für die genannten Probleme finden.

Literatur

• Frank Gurski, Irene Rothe, Jörg Rothe, Egon Wanke: Exakte Algorithmen für schwere Graphenprobleme, Springer-Verlag, Berlin Heidelberg, 2010, ISBN 978-3-642-04499-1