- Zusammenhang von Graphen
-
Der Zusammenhang ist ein mathematischer Begriff aus der Graphentheorie. Ein Graph, das heißt ein Gebilde aus Knoten und Kanten, heißt zusammenhängend, wenn je zwei Knoten durch eine Kantenfolge des Graphen verbunden werden können. Hier werden weitere Präzisierungen und Verschärfungen sowie verwandte Begriffsbildungen behandelt.
Inhaltsverzeichnis
Definition
Ungerichtete Graphen
Ein ungerichteter Graph G = (V,E) heißt zusammenhängend, falls es zu je zwei beliebigen Knoten v und w aus V einen ungerichteten Weg in G gibt, mit v als Startknoten und w als Endknoten. Die Verbindbarkeit zweier Knoten durch eine Kantenfolge ist offenbar eine Äquivalenzrelation auf der Knotenmenge. Eine Äquivalenzklasse
 bzw. den dadurch definierten Teilgraphen nennt man eine Komponente oder Zusammenhangskomponente. Falls G nicht zusammenhängend ist, nennt man G unzusammenhängend, der Graph zerfällt dann in seine Zusammenhangskomponenten.
bzw. den dadurch definierten Teilgraphen nennt man eine Komponente oder Zusammenhangskomponente. Falls G nicht zusammenhängend ist, nennt man G unzusammenhängend, der Graph zerfällt dann in seine Zusammenhangskomponenten.Es seien A und B Teilmengen der Knotenmenge V. Ein Paar Z = (X,Y), bestehend aus einer Knotenmenge
 und einer Kantenmenge
und einer Kantenmenge  , heißt ein A-B-Trenner, wenn jeder A-B-Weg wenigstens einen Knoten aus X oder eine Kante aus Y enthält. Man sagt dann auch, dass Z die Knotenmengen A und B trennt. In den meisten Anwendungsfällen ist
, heißt ein A-B-Trenner, wenn jeder A-B-Weg wenigstens einen Knoten aus X oder eine Kante aus Y enthält. Man sagt dann auch, dass Z die Knotenmengen A und B trennt. In den meisten Anwendungsfällen ist  oder
oder  . In diesem Fall verzichtet man auf die Erwähnung des leeren Bestandteils von Z und sagt einfach, die Kantenmenge Y bzw. die Knotenmenge X trenne A und B. Sind A = {a} und B = {b} einelementig, so spricht man auch von der Trennung von a und b. Man nennt schließlich Z = (X,Y) einen Trenner für G oder sagte Z trenne G, falls es Knoten
. In diesem Fall verzichtet man auf die Erwähnung des leeren Bestandteils von Z und sagt einfach, die Kantenmenge Y bzw. die Knotenmenge X trenne A und B. Sind A = {a} und B = {b} einelementig, so spricht man auch von der Trennung von a und b. Man nennt schließlich Z = (X,Y) einen Trenner für G oder sagte Z trenne G, falls es Knoten  gibt, die durch Z getrennt werden.
gibt, die durch Z getrennt werden.G heißt k-fach kantenzusammenhängend, wenn es keine maximal (k − 1)-elementige Kantenmenge in G gibt, die G trennt (in Multigraphen kann man Kanten entsprechend ihrer Vielfachheit mehrfach entfernen). Als Kantenzusammenhangszahl eines Graphen G bezeichnet man das größte k, sodass G k-fach kantenzusammenhängend ist.
G heißt k-fach knotenzusammenhängend, wenn es keine maximal (k − 1)-elementige Knotenmenge in G gibt, die G trennt. Statt k-fach knotenzusammenhängend sagt man auch oft kürzer k-fach zusammenhängend oder k-zusammenhängend. Als Knotenzusammenhangszahl eines Graphen G bezeichnet man das größte k, sodass G k-zusammenhängend ist.
Ist U eine Teilmenge der Knotenmenge V mit der Eigenschaft, dass der von U induzierte Teilgraph G[U] von k-zusammenhängend ist und G[W] für jede Knotenmenge
 nicht k-zusammenhängend ist, so nennt man G[U] eine k-Zusammenhangskomponente von G. Eine 1-Zusammenhangskomponente ist genau die bereits oben eingeführte Zusammenhangskomponente und eine 2-Zusammenhangskomponente nennt man Block.
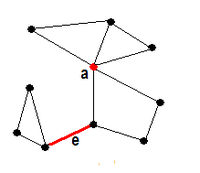
nicht k-zusammenhängend ist, so nennt man G[U] eine k-Zusammenhangskomponente von G. Eine 1-Zusammenhangskomponente ist genau die bereits oben eingeführte Zusammenhangskomponente und eine 2-Zusammenhangskomponente nennt man Block.Ein Knoten a heißt Artikulation oder Gelenkpunkt von G, wenn a ein Trenner für G ist. Eine Kante heißt Brücke von G, wenn sie ihre beiden inzidenten Knoten trennt.
Man bezeichnet den Graphen, der
- als Knotenmenge die Blöcke und Artikulationen von G enthält,
- eine Artikulation a mit einem Block B verbindet, falls a in G zu B gehört und
- sonst keine weiteren Kanten besitzt
als Blockgraph von G.
Gerichtete Graphen
Ein gerichteter Graph G = (V,E) heißt (stark) zusammenhängend von einem Knoten v aus, falls es zu jedem Knoten w einen gerichteten Weg in G mit v als Startknoten und w als Endknoten gibt. G heißt stark zusammenhängend, falls G von jedem Knoten aus zusammenhängend ist.
Ein gerichteter Graph heißt (schwach) zusammenhängend, falls der zugehörige ungerichtete Graph (also der Graph, der entsteht, wenn man jede gerichtete Kante durch eine ungerichtete Kante ersetzt) zusammenhängend ist.
Ein induzierter Teilgraph G[U] für eine Teilmenge
 heißt starke Zusammenhangskomponente von G, falls G[U] stark zusammenhängend ist und kein stark zusammenhängender induzierter Teilgraph von G existiert, der G[U] echt enthält.
heißt starke Zusammenhangskomponente von G, falls G[U] stark zusammenhängend ist und kein stark zusammenhängender induzierter Teilgraph von G existiert, der G[U] echt enthält.Bemerkung: Es gibt genau dann einen Weg mit v als Startknoten und w als Endknoten, wenn es einen Pfad mit v als Startknoten und w als Endknoten gibt. In obigen Definitionen kann man Weg also auch durch Pfad ersetzen.
Wichtige Aussagen und Sätze
Relativ leicht zeigt man folgende Aussagen:
- Ein ungerichteter Graph ist genau dann zusammenhängend, wenn er einen Spannbaum enthält.
- Ein ungerichteter zusammenhängender Graph ist genau dann 2-zusammenhängend, wenn er keine Artikulation besitzt.
- Die Knotenzusammenhangszahl ist höchstens so groß wie Kantenzusammenhangszahl und die Kantenzusammenhangszahl ist höchstens so groß wie der Minimalgrad.
- Der Blockgraph GB eines Graphen G ist ein Wald. GB ist genau dann Baum (also zusammenhängend), wenn G zusammenhängend ist.
Ist G = (V,E) ein ungerichteter Graph und sind A und B Teilmengen von V, so ist die kleinste Mächtigkeit einer A von B trennenden Knotenmenge gleich der größten Mächtigkeit einer Menge disjunkter A-B-Wege. Dieser Satz von Menger (1927) ist eine Verallgemeinerung des Satzes von König (1916), wonach in bipartiten Graphen die Paarungszahl der Knotenüberdeckungszahl entspricht. Man folgert aus ihm leicht den Fächersatz:
Ist B eine Teilmenge von V und a ein Element von
 , so ist die kleinste Mächtigkeit einer a von B trennenden Teilmenge
, so ist die kleinste Mächtigkeit einer a von B trennenden Teilmenge  gleich der größten Mächtigkeit eines a-B-Fächers.
gleich der größten Mächtigkeit eines a-B-Fächers.Ganz ähnlich folgert man: Sind a und b zwei verschiedene Knoten von G, so gilt:
- Sind a und b nicht benachbart, so ist die kleinste Mächtigkeit einer a von b trennenden Teilmenge von
 gleich der größten Mächtigkeit einer Menge disjunkter a-b-Wege in G.
gleich der größten Mächtigkeit einer Menge disjunkter a-b-Wege in G. - Die kleinste Mächtigkeit einer a von b trennenden Kantenmenge
 ist gleich der größten Mächtigkeit einer Menge kantendisjunkter a-b-Wege in G.
ist gleich der größten Mächtigkeit einer Menge kantendisjunkter a-b-Wege in G.
Daraus lässt sich nun die globale Version des Satzes von Menger ableiten:
- G ist genau dann k-zusammenhängend, wenn G zwischen je zwei Ecken k disjunkte Wege enthält.
- G ist genau dann k-fach kantenzusammenhängend, wenn G zwischen je zwei Ecken k kantendisjunkte Wege enthält.
Wichtige Algorithmen
Mittels Tiefensuche lässt sich leicht ein linearer Algorithmus implementieren, der die Zusammenhangskomponenten eines Graphen berechnet und so einen einfachen Test impliziert, ob der Graph zusammenhängend ist. Der Test, ob ein gerichteter Graph von einem Knoten v aus zusammenhängend ist, funktioniert analog. Von Tarjan (1972) stammt ein linearer Algorithmus, der ebenfalls auf Tiefensuche basiert und in gerichteten Graphen die starken Zusammenhangskomponenten und leicht modifiziert in ungerichteten Graphen die Blöcke und Artikulationen berechnet.
Zur Berechnung von Knoten- und Kantenzusammenhangszahl gibt es polynomielle Algorithmen. Dazu kann man beispielsweise Flussalgorithmen verwenden. Allerdings gibt es auch effizientere Algorithmen.
Ein sehr guter, aber komplizierter Algorithmus zur Berechnung des Kantenzusammenhangs eines gerichteten (und damit auch ungerichteten) Graphen mit rationalen Gewichten wurde von H. Gabow entwickelt. (basierend auf der Matroid-Theorie, also einer Menge von Teilbäumen)
Ein leichter und auch für reelle Gewichte geeigneter Algorithmus existiert, entdeckt von Stoer/Wagner und zeitgleich Nagamotchi/Ibaraki. Dieser funktioniert mittels Knotenkontraktion und nur für ungerichtete Graphen.
Ein auf Flussalgorithmen basierender Algorithmus für gerichtete Graphen wurde von Hao/Orlin vorgestellt.
Literatur
- Lutz Volkmann: Fundamente der Graphentheorie, Springer, Wien (Dezember 2001), ISBN 3-211-82774-9
- Reinhard Diestel: Graphentheorie. Springer 2006, ISBN 3-540-21391-0 (elektronische Online-Version)
Wikimedia Foundation.