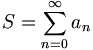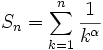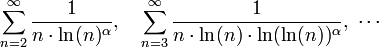Cauchyscher Verdünnungssatz

Das Cauchysche Verdichtungskriterium, auch bekannt als Cauchyscher Verdichtungssatz (nach Augustin Louis Cauchy), ist ein mathematisches Konvergenzkriterium, also ein Mittel zur Entscheidung, ob eine unendliche Reihe konvergent oder divergent ist.

Formulierung

Sei eine unendliche Reihe

$S = \sum_{n=0}^\infty a_n$

mit positiven reellen Summanden a_n gegeben, welche eine monoton fallende Folge bilden.

Dann hat S das gleiche Konvergenzverhalten wie die Reihe

$T = \sum_{k=0}^\infty 2^ka_{2^k}$.

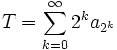Beweisskizze

Die Wirkungsweise dieses Kriteriums kann als Betrachtung von Ober- und Untersummen der zu untersuchenden Reihe gedacht werden. Die Folge 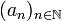$(a_n)_{n\in\N}$ wird in Blöcke aufsteigender Länge aufgeteilt und in jedem Block gegen Maximum und Minimum abgeschätzt. Da die Folge 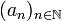$(a_n)_{n\in\N}$ als monoton fallend vorausgesetzt wurde, ist das Maximum mit dem ersten und das Minimum mit dem letzten Folgenglied eines jeden Blockes identisch.

Das Kriterium ergibt sich nun aus dem Majorantenkriterium. Die gängigste Blockaufteilung ist die nach Zweierpotenzen mit Blöcken 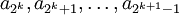$a_{2^k}, a_{2^k+1},\dots,a_{2^{k+1}-1}$. Um Konvergenz nachzuweisen, konstruiert man die Majorante 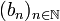$(b_n)_{n\in\N}$ durch

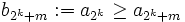$b_{2^k+m}:=a_{2^k}\ge a_{2^k+m}$ für 0≤m<2^k.

Zu jedem Index k enthält die Majorante 2^k Glieder mit demselben Wert 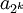$a_{2^k}$, die Majorante konvergiert also genau dann, wenn 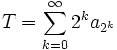$T = \sum_{k=0}^\infty 2^ka_{2^k}$ konvergiert.

Um Divergenz nachzuweisen, konstruiert man die Minorante 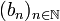$(b_n)_{n\in\N}$ durch

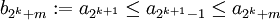$b_{2^k+m}:=a_{2^{k+1}}\le a_{2^{k+1}-1}\le a_{2^k+m}$ für 0≤m<2^k.

Zu jedem Index k enthält die Minorante 2^k Glieder mit demselben Wert 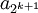$a_{2^{k+1}}$, die Minorante divergiert also genau dann, wenn 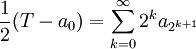$\frac12(T-a_0) = \sum_{k=0}^\infty 2^ka_{2^{k+1}}$ divergiert.

Anwendung

Eine Anwendung liegt bei den allgemeinen harmonischen Reihen. Für ein fixiertes α > 0 hat

$S_n = \sum_{k=1}^n \frac1{k^\alpha}$

das gleiche Konvergenzverhalten wie

$T_n = \sum_{k=0}^n 2^k\frac1{(2^k)^\alpha}=\sum_{k=0}^n (2^{1-\alpha})^k$.

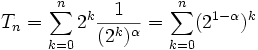T_n ist ersichtlich eine geometrische Reihe mit Faktor q = 2^{1 − α}. Aus deren Konvergenzverhalten folgt, dass für α > 1 Konvergenz, sonst Divergenz, vorliegt.

Analog ergibt sich für die noch langsamer konvergierenden bzw. divergierenden Reihen

$\sum_{n=2}^\infty\frac1{n\cdot \ln(n)^\alpha},\quad \sum_{n=3}^\infty\frac1{n\cdot \ln(n)\cdot \ln(\ln(n))^\alpha},\;\cdots$

für α > 1 Konvergenz, sonst Divergenz.