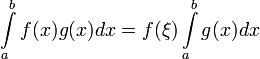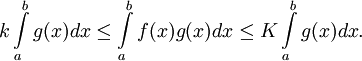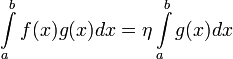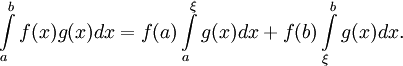Cauchyscher Mittelwertsatz
- Cauchyscher Mittelwertsatz
-
Der Mittelwertsatz der Integralrechnung (auch Cauchyscher Mittelwertsatz genannt) ist ein wichtiger Satz der Analysis. Er erlaubt es, Integrale abzuschätzen, ohne den tatsächlichen Wert auszurechnen und liefert einen einfachen Beweis des Fundamentalsatzes der Analysis. Hier wird das Riemann-Integral betrachtet. Die Aussage lautet dann:
Seien ![f,g:[a,b] \rightarrow \mathbb{R}](/pictures/dewiki/56/8284d1cd3a423737d6351cd0a6d348c4.png) stetige Funktionen und weiterhin
stetige Funktionen und weiterhin 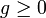 . Dann existiert ein
. Dann existiert ein ![\xi \in [a,b]](/pictures/dewiki/102/f83ba3f626ed0ec9d1df2f3139d398d0.png) , so dass
, so dass
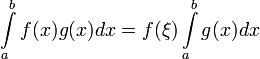
gilt. Manche Autoren bezeichnen die obige Aussage als erweiterten Mittelwertsatz und die Aussage für g = 1 als Mittelwertsatz oder ersten Mittelwertsatz.
Beweis
Seien k und K das Infimum bzw. das Supremum von f auf [a,b], so folgt aus 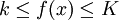 und der Monotonie und Linearität des Riemann-Integrals:
und der Monotonie und Linearität des Riemann-Integrals:
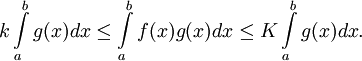
Es gibt also ein ![\eta \in [k,K]](/pictures/dewiki/51/3a38d4f17a754cece65ec8aa5881739b.png) mit
mit
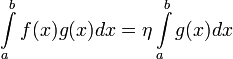
und aus dem Zwischenwertsatz folgt, dass es ein ![\xi \in [a,b] \ \mathrm{mit} \ f(\xi) = \eta](/pictures/dewiki/100/db0446cce1a724425f7369bfa5021c17.png) gibt. Man kann sogar zeigen, dass ξ nie die Grenzen a,b annehmen muss.
gibt. Man kann sogar zeigen, dass ξ nie die Grenzen a,b annehmen muss.
Zweiter Mittelwertsatz der Integralrechnung
Seien ![f,g:[a,b] \rightarrow \mathbb{R}](/pictures/dewiki/56/8284d1cd3a423737d6351cd0a6d348c4.png) Funktionen, f monoton und g stetig. Dann existiert ein
Funktionen, f monoton und g stetig. Dann existiert ein ![\xi \in [a,b]](/pictures/dewiki/102/f83ba3f626ed0ec9d1df2f3139d398d0.png) , so dass
, so dass
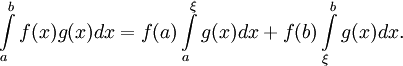
Im Fall, dass f sogar stetig differenzierbar ist, kann man 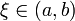 wählen.
wählen.
Beweis
Der Beweis erfordert partielle Integration, den Fundamentalsatz der Analysis und den obigen Satz.
Literatur
- Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. Vieweg, Braunschweig 72004. ISBN 3-528-67224-2
- Harro Heuser, Lehrbuch der Analysis. Teil 1. 8. Auflage, B. G. Teubner, Stuttgart 1990. ISBN 3-519-12231-6
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Mittelwertsatz der Integralrechnung — Zur geometrischen Deutung des Mittelwertsatzes Der Mittelwertsatz der Integralrechnung (auch Cauchyscher Mittelwertsatz genannt) ist ein wichtiger Satz der Analysis. Er erlaubt es, Integrale abzuschätzen, ohne den tatsächlichen Wert auszurechnen… … Deutsch Wikipedia
Fundamentalsatz der Differential- und Integralrechnung — Der Fundamentalsatz der Analysis, auch bekannt als Hauptsatz der Differential und Integralrechnung (kurz: „HDI“), bringt die beiden grundlegenden Konzepte der Analysis, nämlich das der Integration und das der Differentiation, miteinander in… … Deutsch Wikipedia
Hauptsatz der Analysis — Der Fundamentalsatz der Analysis, auch bekannt als Hauptsatz der Differential und Integralrechnung (kurz: „HDI“), bringt die beiden grundlegenden Konzepte der Analysis, nämlich das der Integration und das der Differentiation, miteinander in… … Deutsch Wikipedia
Hauptsatz der Differential- und Integralrechnung — Der Fundamentalsatz der Analysis, auch bekannt als Hauptsatz der Differential und Integralrechnung (kurz: „HDI“), bringt die beiden grundlegenden Konzepte der Analysis, nämlich das der Integration und das der Differentiation, miteinander in… … Deutsch Wikipedia
Newton-Leibniz-Formel — Der Fundamentalsatz der Analysis, auch bekannt als Hauptsatz der Differential und Integralrechnung (kurz: „HDI“), bringt die beiden grundlegenden Konzepte der Analysis, nämlich das der Integration und das der Differentiation, miteinander in… … Deutsch Wikipedia
![f,g:[a,b] \rightarrow \mathbb{R}](/pictures/dewiki/56/8284d1cd3a423737d6351cd0a6d348c4.png) stetige Funktionen und weiterhin
stetige Funktionen und weiterhin 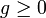 . Dann existiert ein
. Dann existiert ein ![\xi \in [a,b]](/pictures/dewiki/102/f83ba3f626ed0ec9d1df2f3139d398d0.png) , so dass
, so dass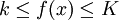 und der Monotonie und Linearität des Riemann-Integrals:
und der Monotonie und Linearität des Riemann-Integrals:![\eta \in [k,K]](/pictures/dewiki/51/3a38d4f17a754cece65ec8aa5881739b.png) mit
mit![\xi \in [a,b] \ \mathrm{mit} \ f(\xi) = \eta](/pictures/dewiki/100/db0446cce1a724425f7369bfa5021c17.png) gibt. Man kann sogar zeigen, dass ξ nie die Grenzen a,b annehmen muss.
gibt. Man kann sogar zeigen, dass ξ nie die Grenzen a,b annehmen muss.![f,g:[a,b] \rightarrow \mathbb{R}](/pictures/dewiki/56/8284d1cd3a423737d6351cd0a6d348c4.png) Funktionen, f monoton und g stetig. Dann existiert ein
Funktionen, f monoton und g stetig. Dann existiert ein ![\xi \in [a,b]](/pictures/dewiki/102/f83ba3f626ed0ec9d1df2f3139d398d0.png) , so dass
, so dass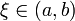 wählen.
wählen.