Integralbild

Ein Integralbild dient der schnellen Berechnung von Pixelsummen innerhalb rechteckiger Ausschnitte von Bildern. Der Begriff ist abgeleitet von dem Konzept der diskreten Integration.

Ursprung

Das Verfahren basiert auf Konzept der Summed Area Tables, das 1984 für das Texture Mapping entwickelt wurde^[1]. Paul Viola und Michael Jones wendeten das Verfahren 2001 erstmals für die Bildverarbeitung an^[2].

Definition

In jedem Punkt des Integralbildes steht die Summe aller Pixel innerhalb des Rechtecks zwischen dem aktuellen Punkt und dem Ursprung des Bildes. In Punkt (x,y) steht also die Summe I_Σ der Pixel innerhalb des Rechtecks, das von den Punkten (0,0), (x,0), (0,y) und (x,y) aufgespannt wird.

$I_{\Sigma}(x,y) = \sum_{i=0}^{i\leq x} \sum_{j=0}^{j\leq y} I(i,j)$

Das Integralbild lässt sich effektiv in einem Durchlauf berechnen, da sich die Summe für einen Pixel immer aus der Vorgängersumme plus dem neuen Pixel ergibt.

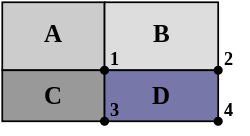
Um die Pixelsumme einer beliebigen Fläche des Ursprungsbildes zu berechnen, muss auf nur 4 Punkte im Integralbild zugegriffen werden.

Beispiel

Die Pixelsumme der Fläche D im nebenstehendes Bild berechnet sich gemäß

$I_\Sigma(\mathrm{Fl\ddot ache}_D) = I_\Sigma(P_1) +I_\Sigma(P_4) - I_\Sigma(P_2) - I_\Sigma(P_3)$

Der große Vorteil dieses Verfahrens ist, dass unabhängig von der Größe der Fläche für die Berechnung der Pixelsummen des Ursprungsbildes immer nur ein Wert aus 4 Pixelwerten des Integralbildes berechnet werden muss.

Videovorträge

• eine theorie hinter dem Integral Bild algorithmus

Einzelnachweise

1. ↑ Franklin C. Crow: Summed-Area Tables for Texture Mapping, Computer Graphics, Volume18, Number 3 Juli 1984
2. ↑ Paul Viola, Michael Jones: Rapid Object Detection using Boosted Cascade of Simple Features