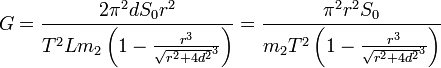Cavendish-Experiment

Die Gravitationswaage ist das Messinstrument in einem physikalischen Experiment zur Bestimmung der Gravitationskonstanten G , welche die Stärke des Feldes der Anziehung, die von einer Masse auf andere Massen ausgeht, festlegt. Sie gibt also ein Maß für die Stärke der Gravitation. 1798 benutzte Henry Cavendish eine solche Apparatur, um zum ersten Mal die Gravitationskonstante zu messen und damit die Masse der Erde bestimmen zu können. Allerdings ging es Cavendish darum, die mittlere Dichte der Erde zu bestimmen.

Aufbau

Cavendish beim Durchführen von Experimenten in seinem Heimlabor.

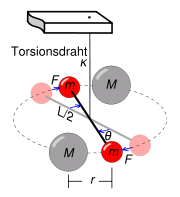Torsionskonstruktion, die von John Michell vorgeschlagen und in Experimenten angewandt wurde.

Im Wesentlichen handelt es sich dabei um eine Drehwaage. Dies bedeutet, dass der Betrag des Winkels, um den ein Draht aus seiner Ruheform verdreht wird, Auskunft über das wirkende Drehmoment gibt. Hieraus lässt sich die Kraft berechnen. Konkret: In der Mitte hängt ein Draht, an dem waagerecht ein Stab angebracht ist. An diesem sind in der Mitte ein Spiegel (parallel zum Draht) und zwei kleine Massen an den Enden befestigt. Davor steht eine Lichtquelle, die einen relativ schmalen Lichtstrahl (heutzutage meist ein Laser) emittiert. Dieser ist auf den Draht gerichtet und wird vom schmalen Spiegel an einen entfernten Schirm reflektiert. Findet nun eine Auslenkung der Massen aus der Ruhelage statt, dann kann man dies durch eine Verschiebung des abgebildeten Lichtpunktes feststellen.

Experiment

Vorbereitung:

• Man muss die Hebellänge 2d, Entfernung zum Schirm L und die Masse m₁ kennen.

Durchführung:

• Man positioniert zwei große Massen m₂ im gleichen Abstand von Massenmittelpunkt zu Massenmittelpunkt r, der möglichst senkrecht zum Stab sein sollte.
• Die Massen ziehen sich an und der Stab dreht sich leicht, wonach er in eine gedämpfte Drehschwingung mikroskopischen Ausmaßes verfällt. Man beobachtet, wie sich der abgebildete Lichtpunkt um einen von der Ruhelage um dem Abstand S₀ verschiedenen Punkt einpendelt.
• Man misst diesen Abstand (und gegebenenfalls die Schwingungsdauer)
• Man wiederholt den Versuch mit anderen Massen und Abständen zur Fehlerreduzierung

Rechnung

Drehmoment: Die Anziehung der Massen ist eine Kraft, diese bewirkt ein Drehmoment 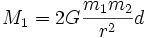$M_1 = 2 G \frac{m_1 m_2}{r^2} d$ auf den Stab. (Genaugenommen gibt es auch ein entgegengesetztes Moment 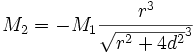$M_2 = -M_1 \frac{r^3}{\sqrt{r^2+4d^2}^3}$, welches durch Anziehung der kleinen Kugeln durch die weiter entfernt liegenden großen Kugeln zustande kommt). Der Verdrehung durch M_res = M₁ + M₂ wirkt die Festigkeit des Drahtes entgegen, je größer der Drehwinkel θ wird, desto mehr Widerstand gibt es. Diese Gegenwirkung ist proportional zum Winkel 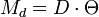$M_d = D \cdot \Theta$, den Proportionalitätsfaktor D nennt man Direktionsmoment.

Direktionsmoment: Man kann einen elastischen Stoff mit konstantem D zu harmonischen Drehschwingungen anregen, dabei ist die Kreisfrequenz 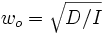$w_o = \sqrt{D/I}$ nur abhängig von Festigkeit und Trägheitsmoment. Dieses berechnet sich hier einfach I = 2m₁d². Aus 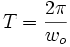$T = \frac{2 \pi}{w_o}$ folgt für die Schwingungsdauer 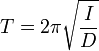$T = 2 \pi \sqrt{ \frac{I}{D} }$. Also ist $D = \frac{4 \pi^2 I} {T^2}$.

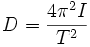Auslenkung: Wie bei allen Spiegeln ist der Drehwinkel der Abbildung doppelt so groß wie der Drehwinkel des Spiegels. Wenn man einen leicht gewölbten Schirm annimmt, ist also der Winkel, um den der Draht gedreht wurde $\Theta = \frac{S_0}{2 L}$.

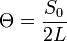Gleichgewicht: Im Gleichgewicht zwischen Anziehung und rücktreibender Kraft muss gelten M_res = M_d. Also 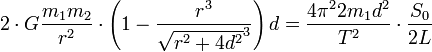$2 \cdot G \frac{m_1 m_2}{r^2} \cdot \left(1 - \frac{r^3}{\sqrt{r^2+4d^2}^3}\right) d = \frac{4 \pi^2 2m_1 d^2}{T^2} \cdot \frac{S_0}{2 L}$. Jetzt ist die Gravitationskonstante G durch bloßes Umformen errechenbar. Letztendlich gilt dann mit L = 2d

$G = \frac{2\pi^2 d S_0 r^2}{T^2 L m_2 \left(1 - \frac{r^3}{\sqrt{r^2 + 4 d^2}^3}\right)} = \frac{\pi^2 r^2 S_0}{m_2 T^2 \left(1 - \frac{r^3}{\sqrt{r^2 + 4 d^2}^3}\right)}$

Relevanz

Der übermäßig erscheinende Aufwand ist vor allem durch die Schwäche der Gravitation 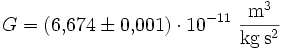$G = (6{,}674\pm 0{,}001) \cdot 10^{-11}~\mathrm{\frac{m^3}{kg\,s^2}}$ zu erklären. Trotzdem verfügen einige Schulen und alle Physik-Institute über einen solchen Apparat. Bei einer selbstgebauten Apparatur ist aber ein relativer Fehler von 20% schon eine gute Leistung.