Kugelbedingung

In der Mathematik ist eine Kugelbedingung eine Eigenschaft einer Menge Ω eines metrischen Raums, in der Regel des $\R^n$. Anschaulich erfüllt Ω die Kugelbedingung, wenn man an jeden Randpunkt eine Kugel so anlegen kann, dass der Schnitt des Randes mit dieser Kugel nur ebendieser Punkt ist. Je nachdem, ob diese Kugel in der Menge oder außerhalb liegt, spricht man von einer inneren bzw. äußeren Kugelbedingung.

Kugelbedingungen finden beispielsweise Anwendung bei der Formulierung von Bedingungen an die Lösbarkeit des Dirichlet-Problems mit der Poissongleichung.

Mathematische Formulierung

Äußere Kugelbedingung in x₁, innere (und äußere) Kugelbedingung in x₂

Ω erfüllt in x₀ eine innere Kugelbedingung, wenn gilt:

$\exists \, x \in \Omega,\, \varepsilon > 0: B_\varepsilon(x) \subset \overline{\Omega} \and B_\varepsilon(x) \cap \partial \Omega = \{x_0\}$

Umgekehrt erfüllt Ω in x₀ eine äußere Kugelbedingung, wenn gilt:

$\exists \, x \in \Omega^c,\, \varepsilon > 0: B_\varepsilon(x) \cap \overline{\Omega} = \{x_0\}$

Dabei bezeichnet B_ε(x) die Kugel um x mit Radius ε. Gilt diese Behauptung für jeden Punkt x₀, so sagt man, dass Ω die Kugelbedingung erfüllt. Kann außerdem in jedem Punkt derselbe Radius ε verwendet werden, sagt man, dass die Kugelbedingung gleichmäßig erfüllt ist.

Beispiele

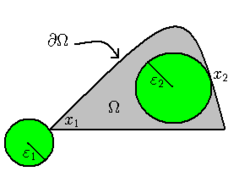
Das Vorliegen einer Kugelbedingung stellt eine gewisse Glattheit des Randes sicher. Offenbar erfüllen die Punkte auf den Kanten eines Würfels keine innere Kugelbedingung. Die inneren Flächenpunkte einer Würfeloberfläche erfüllen offenbar eine Kugelbedingung, aber nicht gleichmäßig, da man mit dem Radius kleiner werden muss, wenn man sich mit dem Punkt einer Kante nähert. In nebenstehender Zeichnung genügt Ω einer gleichmäßigen äußeren Kugelbedingung, wie leicht aus der Konvexität der Menge Ω folgt. In den spitzen Ecken wie x₁ liegt keine innere Kugelbedingung vor.

Literatur

• Pierluigi Colli, Claudio Verdi, Augusto Visintin (Hrsg.): Free boundary problems. Theory and applications. Birkhäuser, Basel u. a. 2004, ISBN 3-7643-2193-8, S. 232.