Rastriginfunktion

Plot der Rastriginfunktion mit zwei Variablen.

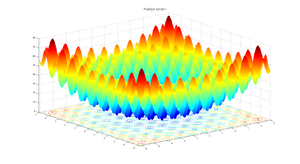
Die Rastriginfunktion ist eine nichtkonvexe Funktion aus dem Bereich der mathematischen Optimierung. Sie wird zur Performanceanalyse in Optimierungsalgorithmen eingesetzt. Die Rastrigin Funktion ist ein typisches Beispiel einer nichtlinearen multimodalen Funktion. Sie wurde zuerst von Rastrigin ^[1] als eine 2-dimensionale Funktion vorgeschlagen und wurde von Mühlenbein ^[2] verallgemeinert.

Diese Funktion ist ein ziemlich schweres Problem wegen ihres großen Suchraumes und der hohen Anzahl lokaler Minima .

Die Rastriginfunktion ist definiert durch:

$f(\mathbf{x}) = A n + \sum_{i=1}^n \left[x_i^2 - A\cos(2 \pi x_i)\right]$

wobei A = 10 und $x_i\in[-5.12,5.12]$. Sie hat ein globales Minimum bei $\mathbf{x} = \mathbf{0}$ mit $f(\mathbf{x})=0$.

Einzelnachweise

1. ↑ A. Törn and A. Zilinskas. "Global Optimization". Lecture Notes in Computer Science, Nº 350, Springer-Verlag, Berlin, 1989.
2. ↑ H. Mühlenbein, D. Schomisch and J. Born. "The Parallel Genetic Algorithm as Function Optimizer ". Parallel Computing, 17, pages 619–632, 1991.

Weblinks

• Rastriginfunktion in der Programmierung (englisch)
• Kurzbeschreibung Rastriginfunktion (englisch)