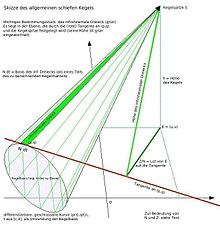
Schiefer Kegel

Schiefkegel

Die Basis des allgemeinen Schiefkegels ist eine geschlossene Kurve mit der Parameter-Darstellung x(t):= p(t) und y(t):= q(t), wobei p und q im Intervall [c,d] differenzierbar sind (bis auf höchstens endlich viele Ausnahmen), außerdem: p(c) = p(d) und q(c) = q(d). Der Punkt E = (u,v) liegt in der Kurven-Ebene, die Kegelspitze S steht im Abstand h senkrecht über E, also S = (u,v,h). Der folgende Formalismus gilt auch für nicht geschlossene Kurven, dann spricht man besser von Segeln als von Kegeln (Dreiecks-Segeln, geschwungenen Dreiecken). Um die Formeln übersichtlich zu halten, wird die Ableitung nach t (wie in der Physik üblich) mit einem Punkt versehen.

Mantel des allgemeinen Schiefkegels

Die Formel für die Mantelfläche M des allgemeinen Schiefkegels gleicht der des schiefen Ellipsenkegels (abgesehen von den Integrationsgrenzen):

$M = \frac{1}{2}\int\limits_c^d\sqrt{Z(t)^2 + h^2\cdot N(t)^2}\mathrm dt$

Hier bedeuten

$Z(t) = (p-u)\cdot\dot{q} - (q-v)\cdot\dot{p}$

und

$N(t) = \sqrt{\dot{p}^2+\dot{q}^2}$

Man könnte mit diesem Formalismus auch den Pyramiden-Mantel berechnen (die Pyramide als „Kegel“ mit quadratischer Basis), aber hier führt die Elementar-Geometrie schneller zum Ziel.

Die geometrische Bedeutung von Z und N

von Z

Das Radizieren einer Funktion f über [c,d] erfordert Sorgfalt, denn die Quadratwurzel aus f² ist mehrdeutig, sogar unendlich vieldeutig. Um das einzusehen, braucht man nur an einer beliebigen Stelle a (die nicht Nullstelle von f ist) den Wert f(a) in -f(a) umzukehren. Geometrisch bedeutsam sind die Wurzeln |f| und f. Wenn in der Formel für den Mantel eines allgemeinen Schiefkegels die Höhe h gegen Null strebt, entsteht der Ausdruck

$M = \frac{1}{2}\int\limits_c^d\sqrt{Z(t)^2}\mathrm dt$

und insbesondere für die Wurzel |Z(t)|:

$M = \frac{1}{2}\int\limits_c^d|Z(t)|\mathrm dt$

geometrisch gesehen ist das die Fläche des „zusammengefalteten“ Kegelmantels in der xy-Ebene (wo die Kegelbasis liegt). Für die Wurzel Z(t) hingegen ergibt sich

$M = \frac{1}{2}\int\limits_c^dZ(t)\mathrm dt = \frac{1}{2}\int\limits_c^d((p - u)\cdot\dot{q} - (q - v)\cdot\dot{p} )\mathrm dt = \frac{1}{2}\int\limits_c^d (p\dot{q} - \dot{p} q)\mathrm dt$

weil die bestimmten Integrale über die Ableitungen von uq und vp Null sind. Das folgt aus der Nebenbedingung p(c) = p(d) und q(c) = q(d). Geometrisch gesehen handelt es sich hierbei um die Fläche der Kegelbasis. Durch partielle Integration (und Beachtung von p(c)q(c) = p(d)q(d)) gewinnt man die Gleichung:

$M = \frac{1}{2}\int\limits_c^d(p\dot{q} - \dot{p}q)\mathrm dt = \int\limits_c^d p\dot{q}\mathrm dt$

Der rechte Ausdruck besticht durch seine Kürze, ist aber unpraktisch, weil sich der scheinbar komplizierte linke Ausdruck besser auswerten lässt. Die Fläche zwischen den Tangenten von E an die Kegelbasis (die Basis selbst nicht mitgerechnet), also die Fläche des Tangenten-Zipfels, ergibt sich aus

$M = \frac{1}{4}\int\limits_c^d(|Z(t)| - Z(t))\mathrm dt$

Der Faktor ¼ (statt ½) besagt, dass die Fläche des Tangentenzipfels nur einmal gezählt wird (statt doppelt wie beim zusammengefalteten Kegelmantel, bei dem die E zugewandte und die E abgewandte Mantelfläche übereinander liegen). Wenn E auf dem Rand oder innerhalb der Kegelbasis liegt, verschwindet M. Dann nämlich fallen Basis und zusammengefalteter Mantel in eins.

von N

Ndt ist das Integrationselement des Umfangs der Kegelbasis (siehe Grafik). Der Umfang der Kegelbasis ergibt sich daher zu

$U = \int\limits_c^d|N(t)|\mathrm dt$

Wenn man nur N(t) als Integranden wählt (statt |N(t)|), kann es vorkommen, dass das Integral verschwindet. Beispiel: Die Astroide (Sternkurve) hat die Parameterdarstellung p(t) = a cos(t)³, q(t) = a sin(t)³ über [0,2Π]. Dann ist N(t)² = 9a² sin(t)² cos(t)². Für N(t) = 3a sin(t) cos(t) verschwindet das Integral über [0,2Π]. Für |N(t)| jedoch ergibt sich

$U = 3a\int\limits_0^{2\pi}|\sin(t)\cdot\cos(t) |\mathrm dt = 12a\int\limits_0^{\frac{\pi}{2}}\sin(t)\cdot\cos(t)\mathrm dt = 6a$

von Z/N

Der Quotient misst den Abstand des Höhenfußpunktes E = (u,v) von der Kurven-Tangente an (p,q) in Abhängigkeit von t (siehe Grafik). Die allgemeine Gleichung der Tangente an (p,q) lautet

$(p - x)\cdot\dot{q} - (q - y)\cdot\dot{p} = 0$

Division durch N führt zur Hesseschen Normalform. Den Abstand des Punktes E = (u,v) von der Tangente gewinnt man dadurch, dass man u und v in die Normalform einsetzt (ohne die Null): das Ergebnis ist Z/N. Beispiel: Die Funktionen p(t) = r cos(t) + m und q(t) = r sin(t) + n über [0,2Π] beschreiben den Kreis r um (m,n). Dann ist Z(t)/N(t) = r + (m-u) cos(t) + (n-v) sin(t). Wenn E in das Zentrum des Kreises rückt, wenn also u = m und v = n, resultiert Z(t)/N(t) = r, d. h. die Lote von E auf die Kreistangenten sind die Radiusvektoren der Länge r.

Beispiel: Schiefer Kreiskegel

Die Parameterdarstellung des Kreises r lautet: p(t) = r cos(t), q(t) = r sin(t) über [0,2Π]. Wenn man diese Werte und ihre Ableitungen in die Formel für den Mantel des allgemeinen Schiefkegels einsetzt, erhält man den Ausdruck

$M = \frac{r}{2}\int\limits_0^{2\pi}\sqrt{(r-u\cdot\cos(t)-v\cdot\sin(t))^2 + h^2}\mathrm dt$

Mit einem geeigneten (festen) Winkel w lassen sich u und v darstellen als u = e cos(w) und v = e sin(w), wobei e²:= u²+v², daher gilt nach dem Additionstheorem: u cos(t) + v sin(t) = e cos(w-t), so dass

$M = \frac{r}{2}\int\limits_0^{2\pi}\sqrt{(r-e\cdot\cos(w-t))^2 + h^2}\mathrm dt$

Bei der Integration über den Vollkreis spielt die Wahl von w keine Rolle. Man darf deshalb w = 0 setzen. Der Integrand ist für w = 0 eine bezüglich Π symmetrische Funktion, so dass man nur über den Halbkreis zu integrieren braucht und das Resultat verdoppeln muss, also:

$M = r\int\limits_0^\pi\sqrt{(r-e\cdot\cos(t))^2 + h^2}\mathrm dt$.

Siehe auch

• Schiefer Kreiskegel
• Schiefer Ellipsenkegel