Cipher Block Chaining

Cipher Block Chaining Mode (CBC) ist eine Betriebsart, in der Blockchiffren betrieben werden können. Vor dem Verschlüsseln eines Klartextblocks wird dieser zunächst mit dem im letzten Schritt erzeugten Geheimtextblock per XOR (exklusives Oder) verknüpft.

Allgemeines

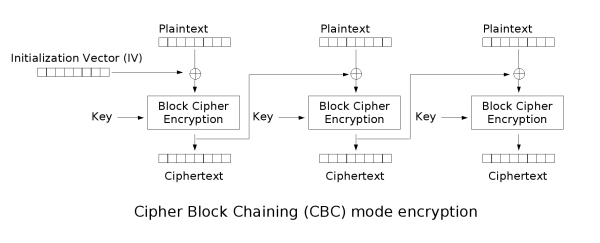
Die Struktur der Verschlüsselung im CBC-Modus ist in nachfolgender Abbildung dargestellt:

Man kann dieses Diagramm auch mathematisch in Formeln ausdrücken, bezeichne dazu E_K die Verschlüsselungsfunktion mit dem Schlüssel K, sei D_K die zugehörige Entschlüsselungsfunktion. Bezeichne P_i den i-ten Klartextblock, C_i den i-ten Geheimtextblock und sei IV der Initialisierungsvektor. Außerdem bezeichne 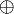$\oplus$ das logische XOR. Dann ist die Verschlüsselung im CBC-Modus wiefolgt rekursiv definiert: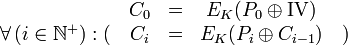

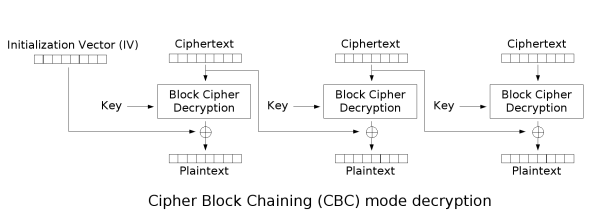
$\begin{matrix} & C_0 & = & E_K(P_0 \oplus \mathrm{IV}) & \\ \forall\left( i \in \mathbb{N}^+ \right):\left(\right. & C_i & = & E_K(P_i \oplus C_{i-1}) & \left.\right) \end{matrix}$

Die Struktur der Entschlüsselung im CBC-Modus ist in nachfolgender Abbildung dargestellt:

Die zugehörige Entschlüsselung ist im CBC-Modus hingegen nicht rekursiv und lautet mit den gleichen Bezeichnungen wie oben:

$\begin{matrix} & P_0 & = & D_K(C_0) \oplus \mathrm{IV} \\ \forall\left( i \in \mathbb{N}^+ \right):\left(\right. & P_i & = & D_K(C_i) \oplus C_{i-1} & \left.\right) \end{matrix}$

Als Initialisierungsvektor (IV) benutzt man

• Entweder einen Zeitstempel
• Oder eine zufällige Zahlenfolge.
• Manche Anwendungen benutzen auch eine vorhersagbare, einfach aufsteigende Zahl, aber dies ist nicht sicher, weil fremde Personen unerwünscht einen Wasserzeichenangriff (watermark attack) auf solche Daten ausführen können.
• Das Modul dm-crypt benutzt zur Generierung des IV das ESS-Verfahren.

Wenn man diesen Initialisierungsvektor geheim überträgt, trägt es nicht zur Sicherheit des Algorithmus bei.

Der CBC-Mode hat einige wichtige Vorteile:

• Klartextmuster werden zerstört.
• Identische Klartextblöcke ergeben unterschiedliche Geheimtexte.
• Verschiedene Angriffe (Time-Memory-Tradeoff und Klartextangriffe) werden erschwert.

Da ein Geheimtextblock nur von dem vorherigen Block abhängt, verursacht ein beschädigter Geheimtextblock, wie beispielsweise ein Bitfehler bei der Datenübertragung, beim Entschlüsseln keinen allzugroßen Schaden, denn es werden nur der betroffene Klartextblock und der darauffolgende Klartextblock falsch dechiffriert. Dies ist unmittelbar aus der Definition der Entschlüsselung und obiger Abbildung ersichtlich, da ein beschädigter Geheimtextblock C_i nur die Klartextblöcke P_i und P_{i + 1} beeinflusst und sich nicht unbeschränkt weiter verbreitet. Trotzdem kann diese beschränkte Vervielfachung nur eines einzigen Bitfehlers im Chiffrat bei CBC eine Vorwärtsfehlerkorrektur des Klartextes erschweren bzw. unmöglichen machen. Genauso verursacht ein beschädigter Initialisierungsvektor beim Entschlüsseln keinen allzugroßen Schaden, da dadurch nur der Klartextblock P₁ beschädigt wird.

Der CBC-Modus ist wesentlich sicherer als der ECB-Modus, vor allem wenn man keine zufälligen Texte hat. Unsere Sprache und andere Dateien, wie z. B. Video-Dateien, sind keinesfalls zufällig, weswegen der ECB-Mode im Gegensatz zum CBC-Mode Gefahren birgt. Generell sollte ein Blockchiffre immer im CBC-Modus betrieben werden - Ausnahmen sollten gut begründet sein.

Beispiel

Klartext: 01 10 ^ ^ | | Aufgeteilt in Blöcke: B₁ B₂

Schlüssel: 11 Init. Vektor (IV): 01

Zur Vereinfachung wird als Codierfunktion + (plus) verwendet (dementsprechend als Decodierfunktion - (minus)) und Überträge mitgezogen

Verschlüsselung

Verschlüsselung (Block 1)

B₁ 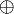$\oplus$ IV = 01 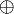$\oplus$ 01 = 00 = C₁' C₁' + Schlüssel = 00 + 11 = 11 = C₁

Verschlüsselung (Block 2)

B₂ 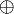$\oplus$ C₁ = 10 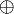$\oplus$ 11 = 01 = C₂' C₂' + Schlüssel = 01 + 11 = 100 = C₂

Verschlüsselter Text = C₁ C₂ = 11 100

Betrachtet man die Verschlüsselung von B₂, sieht man, dass dazu C₁ benötigt wird. Generell bedeutet das, dass für eine Verschlüsselung von B_i der Codeblock C_{i − 1} benötigt wird. Eine Parallelisierung des Kodiervorgangs fällt damit aus.

Entschlüsselung

Verschlüsselter Text: 11 100 ^ ^ | | Aufgeteilt in Blöcke: C₁ C₂

Entschlüsselung (Block 1)

C₁ - Schlüssel = 11 - 11 = 00 = C₁' C₁' 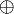$\oplus$ IV = 00 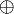$\oplus$ 01 = 01 = B₁

Entschlüsselung (Block 2)

C₂ - Schlüssel = 100 - 11 = 01 = C₂' C₂' $\oplus$ C1 = 01 $\oplus$ 11 = 10 = B₂

Klartext = B₁ B₂ = 01 10

Betrachtet man die Entschlüsselung von C₂, sieht man, dass B₁ dafür nicht benötigt wird, sondern lediglich C₁. Generell bedeutet das, dass für eine Dekodierung von C_i nur C_{i − 1} benötigt wird. Damit ist eine Parallelisierung des Entschlüsselungsvorgangs möglich.

Integritätssicherung mit CBC, CBC-MAC

Struktur zur CBC-MAC Berechnung

CBC kann auch zur Integritätssicherung benutzt werden, indem der letzte mit CBC verschlüsselte Block als MAC (dem sogenannten CBC-MAC oder CBC-Restwert) an die ursprüngliche unverschlüsselte Nachricht angehängt und diese samt diesem MAC versandt wird. Der Empfänger kann mit Hilfe des CBC-Algorithmus den CBC-MAC der empfangenen Nachricht berechnen und nun vergleichen, ob der gerade selbst berechnete Wert mit dem an der Nachricht angehängten übereinstimmt.

Siehe auch

• Cipher Feedback Mode
• Output Feedback Mode
• Electronic Code Book Mode

Literaturhinweis

• Reinhard Wobst: Abenteuer Kryptologie. ISBN 3-8273-1413-5.