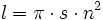Clacksons Spiralenformel (nach Stephen Clackson) [1]:
zum Abschätzen beim Schmieden der benötigten Länge l von Stangenmaterial zur Herstellung einer Spirale mit n Runden und einem Abstand s zwischen den Runden.
Die Formel nähert die Kurvenlänge der ersten n Runden einer Archimedischen Spirale durch folgende Gleichung an:
.Wikimedia Foundation.
Clacksonsche Spiralenformel — Clacksons Spiralenformel (nach Stephen Clackson) [1]: zum Abschätzen beim Schmieden der benötigten Länge l von Stangenmaterial zur Herstellung einer Spirale mit n Runden und einem Abstand s zwischen den Runden. Die Formel nähert die Kurvenlänge… … Deutsch Wikipedia
Clackson — Stephen Gregory Clackson (* 23. April 1961 in Taunton) ist ein britischer Physiker und Kristallograph. Clackson erkannte, dass die meisten Gitterebenen in einem zylindrisch verformten Kristallgitter auf Archimedischen Spiralen liegen müssen [1].… … Deutsch Wikipedia
Stephen Clackson — Stephen Gregory Clackson (* 23. April 1961 in Taunton) ist ein britischer Physiker und Kristallograph. Clackson erkannte, dass die meisten Gitterebenen in einem zylindrisch verformten Kristallgitter auf Archimedischen Spiralen liegen müssen [1].… … Deutsch Wikipedia
Stephen Gregory Clackson — (* 23. April 1961 in Taunton) ist ein britischer Physiker und Kristallograph. Clackson erkannte, dass die meisten Gitterebenen in einem zylindrisch verformten Kristallgitter auf Archimedischen Spiralen liegen müssen [1]. Ebenso fand er eine… … Deutsch Wikipedia
Spirale — Die Spirale als Emblem der 20. Olympischen Sommerspiele Eine Spirale oder Schneckenlinie ist eine Kurve, die um einen Punkt oder eine Achse verläuft und sich je nach Laufrichtung von diesem/r entfernt oder annähert … Deutsch Wikipedia
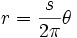