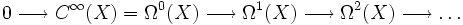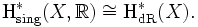De-Rham

Die de-Rham-Kohomologie ist eine Kohomologietheorie für glatte Mannigfaltigkeiten.

Definition

Sei X eine glatte Mannigfaltigkeit und Ω^k(X) die Menge der k-Formen auf X. Die k-te de-Rham-Kohomologiegruppe 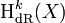$\mathrm H^k_{\mathrm{dR}}(X)$ ist definiert als die k-te Kohomologie des de-Rham-Komplexes:

$0\longrightarrow C^\infty(X)=\Omega^0(X)\longrightarrow\Omega^1(X)\longrightarrow\Omega^2(X)\longrightarrow\ldots$

Die Abbildungen 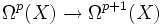$\Omega^p(X)\to\Omega^{p+1}(X)$ sind durch die Cartan-Ableitung gegeben.

Insbesondere gilt 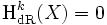$\mathrm H^k_{\mathrm{dR}}(X)=0$ für $k>\dim X.$

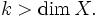
Geschichte

In seiner Pariser Dissertation (1931) bewies Georges de Rham mit seinem Satz eine Vermutung von Élie Cartan, die ihrerseits auf Überlegungen von Henri Poincaré zurückging. Da die Kohomologie eines topologischen Raumes erst einige Jahre später thematisiert wurde, arbeitete er tatsächlich mit der Homologie und dem (aufgrund des Satzes von Stokes) dualen Komplex der n-Ketten.

Homotopieinvarianz

Seien M und N zwei homotopieäquivalente glatte Mannigfaltigkeiten, dann gilt für jedes $p \in \N \cup \{0\}$

$\mathrm H^p_{\mathrm{dR}}(M) \cong \mathrm H^p_{\mathrm{dR}}(N)$.

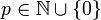
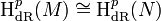Da also zwei homotope, glatte Mannigfaltigkeiten bis auf Isomorphie die gleiche de-Rahm-Kohomologie besitzen, ist diese Kohomologie eine topologische Invariante einer glatten Mannigfaltigkeit. Das ist bemerkenswert, da bei der Definition der de-Rahm-Gruppe die differenzierbare Struktur der Mannigfaltigkeit eine wichtige Rolle spielt. Man hat also erstmal keinen Grund anzunehmen, dass eine topologische Mannigfaltigkeit mit unterschiedlichen differenzierbaren Strukturen dieselben de-Rahm-Gruppen hat.

Satz von de Rham

Er besagt, dass die de-Rham-Kohomologie für kompakte orientierbare Mannigfaltigkeiten natürlich isomorph zur singulären Kohomologie mit Koeffizienten in den reellen Zahlen ist:

$\mathrm H^*_{\mathrm{sing}}(X,\mathbb R)\cong\mathrm H^*_{\mathrm{dR}}(X).$

Beispiele einiger de-Rham-Gruppen

Das Berechnen der de-Rham-Gruppen ist oftmals schwierig, darum folgen nun ein paar Beispiele. Es sei immer vorausgesetzt, dass die betrachteten Mannigfaltigkeiten glatt sind.

• Sei M eine zusammenhängende Mannigfaltigkeit, dann ist 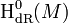$\mathrm H^0_{\mathrm{dR}}(M)$ gleich der Menge der konstanten Funktionen und hat Dimension eins.
• Sei M eine null-dimensionale Mannigfaltigkeit, dann ist die Dimension von 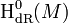$\mathrm H^0_{\mathrm{dR}}(M)$ gleich der Mächtigkeit von M und alle anderen Kohomologiegruppen verschwinden.
• Sei 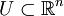$U \subset \R^n$ ein offenes Sterngebiet, dann gilt 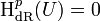$\mathrm H^p_{\mathrm{dR}}(U) = 0$ für alle 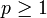$p \geq 1$. Dies ist das Lemma von Poincaré.
• Insbesondere gilt 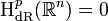$\mathrm H^p_{\mathrm{dR}}(\R^n) = 0$, da der euklidische Raum ein Sterngebiet ist.
• Sei M eine einfach-zusammenhängende Mannigfaltigkeit, dann gilt $\mathrm H_{\mathrm{dR}}^1(M) = 0$.

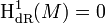Anmerkungen

• Mathematical Subject Classification (2000) 58A12

Literatur

• Bott, Raoul; Tu, Loring W.: Differential forms in algebraic topology. – Berlin, 1982 (Graduate Texts in Mathematics; 82) ISBN 0-387-90613-4
• Jänich, Klaus: Vektoranalysis, Berlin, ⁵2005. ISBN 3-540-23741-0
• Rham, Georges de: Sur l'analysis situs des variétés à n dimensions, J. Math. Pures Appl. (9) 10, 115–200 (1931)
• Weil, André: Sur les théorèmes de de Rham, Comment. Math. Helv., 26, 119–145 (1952); Œuvres II, 17–43