Dedekind domain — In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily … Wikipedia
Ring (mathematics) — This article is about algebraic structures. For geometric rings, see Annulus (mathematics). For the set theory concept, see Ring of sets. Polynomials, represented here by curves, form a ring under addition and multiplication. In mathematics, a… … Wikipedia
Dedekind-infinite set — In mathematics, a set A is Dedekind infinite if some proper subset B of A is equinumerous to A. Explicitly, this means that there is a bijective function from A onto some proper subset B of A. A set is Dedekind finite if it is not Dedekind… … Wikipedia
Dedekind zeta function — In mathematics, the Dedekind zeta function of an algebraic number field K, generally denoted ζK(s), is a generalization of the Riemann zeta function which is obtained by specializing to the case where K is the rational numbers Q. In particular,… … Wikipedia
Dedekind–Hasse norm — In mathematics, in particular the study of abstract algebra, a Dedekind–Hasse norm is a function on an integral domain that generalises the notion of a Euclidean function on Euclidean domains. Contents 1 Definition 2 Integral and principal ideal… … Wikipedia
Ring — Windung; Kringel; Kreis; Reif * * * Ring [rɪŋ], der; [e]s, e: 1. gleichmäßig runder, kreisförmig in sich geschlossener Gegenstand: einen goldenen Ring am Finger tragen. Zus.: Armring, Dichtungsring, Fingerring, Fußring, Gardinenring, Goldring,… … Universal-Lexikon
Ring of integers — In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication. It is a commutative ring, and is the prototypical such by virtue of satisfying only … Wikipedia
Glossary of ring theory — Ring theory is the branch of mathematics in which rings are studied: that is, structures supporting both an addition and a multiplication operation. This is a glossary of some terms of the subject. Contents 1 Definition of a ring 2 Types of… … Wikipedia
Kommutativer Ring — Ring berührt die Spezialgebiete Mathematik Abstrakte Algebra Gruppentheorie Zahlentheorie ist Spezialfall von additive Abelsche Gruppe multiplikative Halbgruppe … Deutsch Wikipedia
Unitärer Ring — Ring berührt die Spezialgebiete Mathematik Abstrakte Algebra Gruppentheorie Zahlentheorie ist Spezialfall von additive Abelsche Gruppe multiplikative Halbgruppe … Deutsch Wikipedia
![\mathbb Z[\sqrt{-5}].](/pictures/dewiki/52/49ff54339b915fabe22898e945d1dd67.png)
![\mathbb Z[T]](/pictures/dewiki/51/37ed16841f74ec2084e251ef48a17a3f.png) (zweidimensional),
(zweidimensional),![\mathbb Z[\sqrt5]](/pictures/dewiki/101/eda3c039b3c1230e72ac79bdb72d38d2.png) (nicht normal),
(nicht normal),![\mathbb Z[T]/(T^2)](/pictures/dewiki/51/359e0079c631b4e84c69ef39b6eea611.png) oder
oder 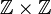 (kein Integritätsbereich).
(kein Integritätsbereich).