Dedekind-Unendlichkeit

Dedekind-Unendlichkeit ist ein Begriff aus der Mathematik, der eine scheinbar paradoxe Eigenschaft unendlicher Mengen einfängt.

Eine endliche Menge M, etwa mit n Elementen, ist niemals zu einer echten Teilmenge gleichmächtig, d.h., es kann keine bijektive Abbildung von M auf eine echte Untermenge U von M geben. Unendliche Mengen haben diese Eigenschaft sehr wohl, so gibt es etwa von der archetypischen unendlichen Menge 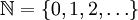${\Bbb N} = \{0,1,2,\ldots\}$ der natürlichen Zahlen eine Bijektion f auf die echte Teilmenge der positiven natürlichen Zahlen, nämlich die Abbildung f(n) = n + 1. Dabei bezeichnet n +1 den Nachfolger der Zahl n; die Addition braucht noch nicht erklärt zu sein.

Richard Dedekind nahm diese Eigenschaft als Grundlage einer Definition des Begriffs "Unendliche Menge". In moderner Terminologie definiert man:

• Eine Menge M heißt Dedekind-unendlich, wenn sie gleichmächtig mit einer echten Teilmenge ist.
• M heißt Dedekind-endlich, wenn M zu keiner echten Teilmenge gleichmächtig ist.

Man kann (mit den ZF-Axiomen, ohne Auswahlaxiom) beweisen, dass die folgenden Aussagen für jede Menge M äquivalent sind:

1. M ist zu einer echten Teilmenge gleichmächtig (also Dedekind-unendlich).
2. M ist zu einer Menge der Form M \ {m} (mit m in M) gleichmächtig.
3. M ist zu einer echten Obermenge gleichmächtig.
4. M enthält eine Kopie der natürlichen Zahlen, das heißt: es gibt eine injektive Funktion von 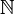$\mathbb N$ nach M.

Insbesondere ist also die Menge 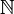${\Bbb N}$ selbst Dedekind-unendlich, ebenso auch jede Menge, die die natürlichen Zahlen als Teilmenge enthält.

Man kann mit Hilfe des Auswahlaxioms zeigen, dass jede unendliche Menge auch Dedekind-unendlich ist. (Die Tatsache, dass jede Dedekind-unendliche Menge auch unendlich ist – oder äquivalent dazu: dass jede endliche Menge auch Dedekind-endlich ist – kann man mit Hilfe der vollständigen Induktion ohne Verwendung des Auswahlaxioms beweisen.)