Depth-First Search

Tiefensuche

Tiefensuche (Depth-First Search) ist in der Informatik ein Verfahren zum Suchen eines Knotens in einem Graphen. Sie zählt zu den uninformierten Suchalgorithmen. Eine Verbesserung der Tiefensuche ist die iterative Tiefensuche.

Allgemeines

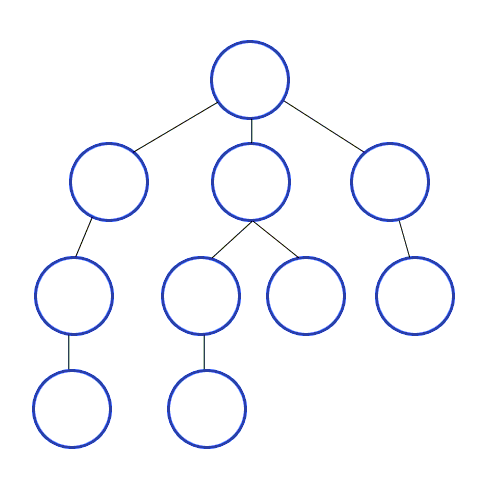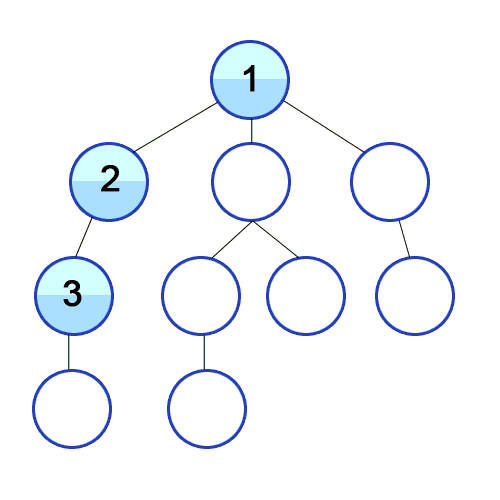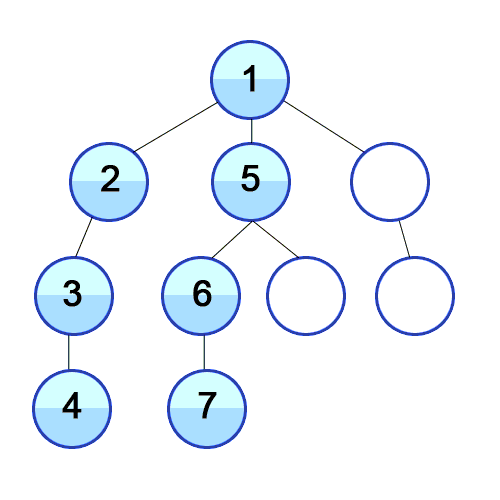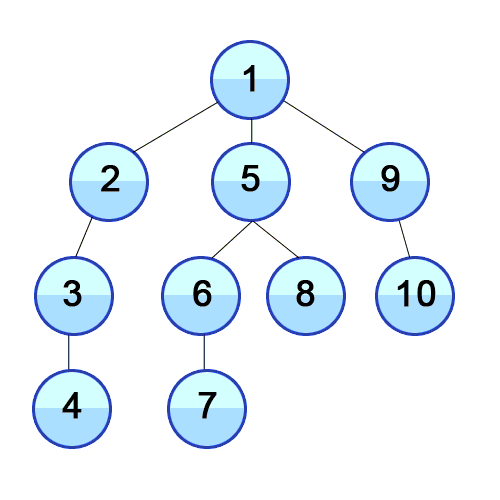
Die Tiefensuche ist eine uninformierte Suche, welche durch Expansion des jeweils ersten auftretenden Nachfolgeknotens im Graph nach und nach vom Startknoten aus weiter in die Tiefe sucht. In welcher Reihenfolge die Nachfolger eines Knotens dabei bestimmt werden, hängt von der Repräsentation der Nachfolger ab. Bei der Repräsentation über eine Adjazenzliste mittels einer verketteten Liste werden beispielsweise die Knoten in der Reihenfolge ihres Eintrags in dieser Liste durchlaufen. Im oben angegebenen Bild wird implizit davon ausgegangen, dass die Nachfolger "von links nach rechts" ausgewählt werden.

Für ungerichtete Graphen sieht das Verfahren wie folgt aus: Zuerst wird ein Startknoten 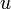$\left. u \right.$ ausgewählt. Von diesem Knoten aus wird nun die erste Kante 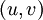$\left( u,v \right)$ betrachtet und getestet, ob der gegenüberliegende Knoten 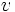$\left. v \right.$ schon entdeckt wurde bzw. das gesuchte Element ist. Ist dies noch nicht der Fall, so wird rekursiv für diesen Knoten die Tiefensuche aufgerufen, wodurch wieder der erste Nachfolger dieses Knotens expandiert wird. Diese Art der Suche wird solange fortgesetzt, bis das gesuchte Element entweder gefunden wurde oder die Suche bei einer Senke im Graph angekommen ist und somit keine weiteren Nachfolgeknoten mehr untersuchen kann. An dieser Stelle kehrt der Algorithmus nun zum zuletzt expandierten Knoten 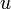$\left. u \right.$ zurück und untersucht den nächsten Nachfolger des Knotens. Sollte es hier keine weiteren Nachfolger mehr geben, geht der Algorithmus wieder Schritt für Schritt zum jeweiligen Vorgänger zurück und versucht es dort erneut.

Ein Beispiel für die Anwendung der Tiefensuche auf einem Baum findet man im oben stehenden Bild.

Algorithmus (informell)

1. Bestimme den Knoten an dem die Suche beginnen soll
2. Expandiere den Knoten und speichere alle Nachfolger in einem Stack
3. Rufe rekursiv für jeden der Knoten in dem Stack DFS (depth first search oder Tiefensuche) auf
   • Falls der Stack leer sein sollte, tue nichts
   • Falls das gesuchte Element gefunden worden sein sollte, brich die Suche ab und liefere ein Ergebnis

Algorithmus (formal)

DFS(node, goal)
{
  if (node == goal)
    return node;
  else
  {
    stack := expand (node)
    while (stack is not empty)
    {
      node' := pop(stack);
      DFS(node', goal);
    }
  }
}

Algorithmusbeispiel: Erzeugen des Tiefensuchwaldes (rekursiv)

Der folgende rekursive Algorithmus erzeugt den Tiefensuchwald eines Graphen G mittels Setzen von Discovery- und Finishing-Times und Färben der Knoten. In Anlehnung an Cormen, Leiserson, Rivest, Stein, Introduction to Algorithms, MIT Press, 2001, werden zunächst alle Knoten weiß gefärbt. Anschließend startet die Tiefensuche per Definition beim alphabetisch kleinsten Knoten und färbt diesen grau. Danach wird, wie oben beschrieben rekursiv dessen weißer Nachbar betrachtet und grau gefärbt. Existiert kein weißer Nachbar mehr, kommt es zum Backtracking, während dessen alle durchwanderten Knoten schwarz gefärbt werden.

DFS(G)
1   for each v of G {        // Alle Knoten weiß färben, Vorgänger auf nil setzen
2      col[v] = 'w';
3      pi[v] = nil;
4   }
5   time = 0;
6   for each u of G          // Für alle weißen Knoten: DFS-visit aufrufen
7      if col[u] == 'w'
8         DFS-visit(u);

DFS-visit(u)
1   col[u] = 'g';            // Aktuellen Knoten grau färben
2   time++;                  // Zeitzähler erhöhen
3   d[u] = time;             // Entdeckzeit des aktuellen Knotens setzen
4   for each v of Adj[u] {   // Für alle weißen Nachbarn des aktuellen Knotens
5       if col[v] == 'w' {
6          pi[v] = u;         // Vorgänger auf aktuellen Knoten setzen
7          DFS-visit(v);      // DFS-visit aufrufen
8       }
9    }
10   col[u] = 's';           // Aktuellen Knoten schwarz färben
11   time++;
12   f[u] = time;            // Finishing-Time des aktuellen Knotens setzen

Eigenschaften

Laufzeit

Da im schlimmsten Fall alle möglichen Pfade zu allen möglichen Knoten betrachtet werden müssen, beträgt die Laufzeit von Tiefensuche 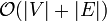$\mathcal{O}(\vert V \vert + \vert E \vert)$, wobei 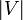$\vert V \vert$ für die Anzahl der Knoten und 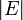$\vert E \vert$ für die Anzahl der Kanten im Graph stehen.

Vollständigkeit

Falls ein Graph unendlich groß ist oder kein Test auf Zyklen durchgeführt wird, so ist Tiefensuche nicht vollständig. Es kann also sein, dass ein Ergebnis - obwohl es existiert - nicht gefunden wird.

Optimalität

Tiefensuche ist insbesondere bei monoton steigenden Pfadkosten nicht optimal, da eventuell ein Ergebnis gefunden wird, zu welchem ein sehr viel längerer Pfad führt als zu einem alternativen Ergebnis. Dafür wird ein solches Ergebnis i.A. deutlich schneller gefunden als bei der (in diesem Fall optimalen, aber sehr viel speicheraufwendigeren) Breitensuche. Als Kombination von Tiefen- und Breitensuche gibt es die iterative Tiefensuche.

Anwendung

Die Tiefensuche ist indirekt an vielen komplexeren Algorithmen für Graphen beteiligt. Einige Beispiele hierfür sind das Finden einer topologischen Sortierung eines Graphen, oder das Finden aller starken Zusammenhangskomponenten eines Graphen.

Siehe auch

• Beschränkte Tiefensuche
• Breitensuche
• Iterative Tiefensuche
• Tiefensuche bei gewichteten Graphen

Literatur

• Thomas H. Cormen, Charles Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms, MIT Press, 2nd edition 2001, ISBN 0262531968
• Stuart Russell, Peter Norvig: Artificial Intelligence: A Modern Approach, 2. Auflage, 2002, Prentice Hall.

Weblinks

• Bebilderte Schritt-für-Schritt-Analyse zur Tiefensuche und schönes Java-Applet
• Java-Applet zur Demonstration
• Interaktives Java-Applet zur Demonstration
• Tiefensuche beim Algorithmus der Woche