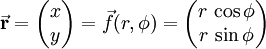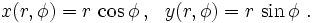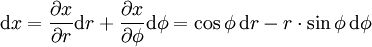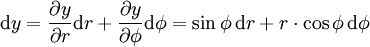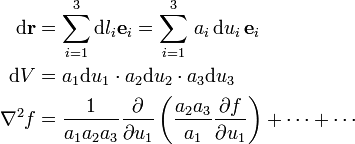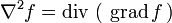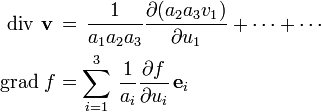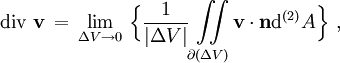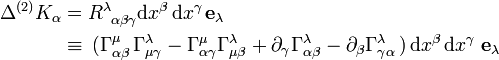Differenzialgeometrie

Die Differentialgeometrie stellt als Teilgebiet der Mathematik die Synthese von Analysis und Geometrie dar.

Inhaltsverzeichnis

1 Historische Entwicklung und aktuelle Anwendungsgebiete
2 Teilgebiete
3 Methoden
4 Literatur
5 Weblinks

Historische Entwicklung und aktuelle Anwendungsgebiete

Etliche grundlegende Arbeiten zur Differentialgeometrie stammen von Carl Friedrich Gauß. In dieser Zeit war die Mathematik noch stark mit verschiedenen Anwendungsgebieten verknüpft. Wichtige Ergebnisse lieferte diese Theorie dabei auf den Gebieten der Kartografie, Navigation und Geodäsie. Es entwickelte sich unter anderem die Kartenprojektionslehre, aus der die Begriffe geodätische Linie und gaußsche Krümmung stammen. Zudem stellte sich C.F. Gauß bereits die Frage, ob die durch Peilung gemessene Winkelsumme eines sehr großen Dreiecks tatsächlich exakt 180 Grad beträgt, und erweist sich damit als Wegbereiter der modernen Differentialgeometrie.

Die moderne Differentialgeometrie findet vor allem in der allgemeinen Relativitätstheorie und in der Satellitennavigation ihre Anwendung. Sie ermöglicht die Beschreibung von Phänomenen wie astronomische Lichtablenkung oder Periheldrehung des Merkur, die durch Experimente bestätigt werden können. Koordinatentransformationen entsprechen in der Relativitätstheorie dem Wechsel von Bezugssystemen, aus denen heraus ein Phänomen beobachtet wird. Dies entspricht damit unterschiedlichen Bewegungszuständen der Messapparatur bzw. des Beobachters.

Ein anderes wichtiges Anwendungsgebiet liegt in der Theorie der Defekte und der Plastizität.

Teilgebiete

Elementare Differentialgeometrie

Die ersten Arbeiten zur Differentialgeometrie beschäftigen sich sowohl mit Kurven als auch mit zweidimensionalen gekrümmten Flächen im dreidimensionalen reellen Anschauungsraum. Geschichtlich gesehen wurde es mit Gauß' Arbeiten erstmals möglich, die Krümmung beispielsweise der zweidimensionalen Oberfläche einer Kugel auch quantitativ zu erfassen.

Eine weitere Motivation zur Entwicklung der elementaren Differentialgeometrie kam auch von dem mathematischen Problem der Minimalflächen her. Die in der Natur vorkommenden Seifenhäute lassen sich als Minimalflächen beschreiben. Die Form bzw. mathematische Darstellung dieser Flächen lässt sich dabei mit den Methoden aus der Variationsrechnung entwickeln. Die geometrischen Eigenschaften dieser Flächen wie Krümmung oder Abstände zwischen beliebigen Punkten auf einer Minimalfläche werden dagegen eher mit den Methoden der Differentialgeometrie berechnet.

Moderne Differentialgeometrie

Die abstrakte Differentialgeometrie entsteht aus der intrinsischen Beschreibung geometrischer Objekte, d. h. der Beschreibung ohne Rückgriff auf einen umgebenden Raum. Der zentrale Begriff ist der der differenzierbaren Mannigfaltigkeit: eine $n$ -dimensionale Mannigfaltigkeit ist ein geometrisches Objekt (genauer: ein topologischer Raum), der lokal in etwa aussieht wie der $n$ -dimensionale reelle Raum. Das klassische Beispiel, das auch die Terminologie motiviert, ist die Erdoberfläche: In kleinen Ausschnitten lässt sie sich durch Karten beschreiben, d. h. kleine Teile „sehen aus wie“ die Ebene. Um aber ein Gesamtbild der Erde zu erhalten, müssen noch die Kartenwechsel beschrieben sein: welche Teile zweier Karten entsprechen einander? Das Attribut differenzierbar bezieht sich nun darauf, dass diese Kartenwechsel differenzierbare Abbildungen sein sollen. Das ermöglicht es, von differenzierbaren Funktionen auf der Mannigfaltigkeit zu sprechen, und die Analysis wird gewissermaßen zur lokalen Theorie, deren globale Entsprechung die Differentialgeometrie ist. Ferner bekommen Differentiale wie z. B. $d f$ , die in der klassischen Differentialgeometrie als „infinitesimale Funktionsdifferenzen“ interpretiert werden, jetzt die Bedeutung von Derivationen, das sind Operatoren, die jedem Vektor $\mathbf v$ des Tangentialbündels die Ableitung der Funktion f nach $\mathbf v$ zuordnen, ${\rm d}f [\mathbf v]:=\frac{\partial f}{\partial \mathbf v}\,.$

Riemannsche Geometrie

Auf einer differenzierbaren Mannigfaltigkeit gibt es keine vordefinierte Längenmessung. Ist sie als zusätzliche Struktur gegeben, spricht man von riemannschen Mannigfaltigkeiten. Diese Mannigfaltigkeiten sind Gegenstand der riemannschen Geometrie, die auch die zugehörigen Begriffe der Krümmung, der kovarianten Ableitung und der Parallelverschiebung auf diesen Mengen untersucht.

Wird dagegen eine verallgemeinerte metrische Struktur - beispielsweise in Form einer Lösung der einsteinschen Feldgleichungen - untersucht, so werden diese Mannigfaltigkeiten einsteinsche -, semi - oder auch pseudo-riemannsche Mannigfaltigkeiten genannt.

Differentialtopologie

Die Differentialtopologie benutzt Mittel der Differentialgeometrie und der Topologie zum Studium topologischer Eigenschaften der betrachteten Mannigfaltigkeiten.

Theorie der Liegruppen

So wie Gruppen auf Mengen basieren, sind Mannigfaltigkeiten die Grundlage der Liegruppen. Die nach Sophus Lie benannten Liegruppen treten an vielen Stellen der Mathematik und Physik als kontinuierliche Symmetriegruppen, beispielsweise als Gruppen von Drehungen des Raumes auf. Das Studium des Transformationsverhaltens von Funktionen unter Symmetrien führt zur Darstellungstheorie der Liegruppen.

Methoden

Koordinatentransformationen

Koordinatentransformationen sind ein wichtiges Werkzeug der Differentialgeometrie, um die Anpassung einer Problemstellung an geometrische Objekte zu ermöglichen. Sollen beispielsweise Abstände auf einer Kugeloberfläche untersucht werden, so werden meist Kugelkoordinaten verwendet. Betrachtet man euklidische Abstände im Raum, so verwendet man dagegen eher kartesische Koordinaten. Mathematisch gesehen ist zu beachten, dass Koordinatentransformationen stets bijektive, unendlich oft stetig differenzierbare Abbildungen sind. Es existiert also immer auch die Inverse zu der betrachteten Koordinatentransformation.

Ein einfaches Beispiel ist der Übergang von kartesischen Koordinaten in der Ebene zu Polarkoordinaten. Jeder Ortsvektor des zweidimensionalen euklidischen Raumes lässt sich bei dieser Darstellung durch die Koordinaten 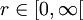$r \in [0, \infty[$ und $\phi \in [0, 2\pi [$ in der folgenden Weise ausdrücken

$\vec {\mathbf r} = \begin{pmatrix} x \\ y \end{pmatrix} = \vec{f}(r,\phi) = \begin{pmatrix} r\,\cos \phi \\ r\,\sin \phi \end{pmatrix}$

x und y werden dabei auch als Komponentenfunktionen von f bezeichnet. Sie berechnen sich in Abhängigkeit von den zwei Koordinaten $(r,φ)$ gemäß:

$x(r,\phi) = r\,\cos \phi\,,\,\,\,\, y(r,\phi) = r\,\sin \phi\,\,.$

Werden nun ganz allgemein alle Koordinaten des neuen Koordinatensystems bis auf eine Koordinate konstant gehalten und die einzelne Koordinate innerhalb des Definitionsbereiches verändert, entstehen im euklidischen Raum Linien, die auch als Koordinatenlinien bezeichnet werden. Im Falle der angegebenen Polarkoordinaten entstehen so bei konstanter $r$ Koordinate konzentrische Kreise mit Radius $r$ um den Koordinatenursprung $(x, y) = (0,0)$ des euklidischen Koordinatensystems. Bei konstanter $φ$ Koordinate entstehen Halbgeraden, die im Koordinatenursprung des euklidischen Koordinatensystems starten und nach 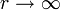$r \rightarrow \infty$ laufen. Mit Hilfe dieser Koordinatenlinien lässt sich in naheliegender Weise für jeden Punkt 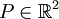$P \in \mathbb{R}^2$ des euklidischen Raumes ein neues, räumlich gedrehtes und wieder rechtwinkliges Koordinatensystem definieren. Man spricht daher bei Polarkoordinaten auch von rechtwinkligen Koordinaten. Die Achsen des gedrehten Koordinatensystems sind dabei gerade die Tangenten an die Koordinatenlinien, die durch den Punkt $P$ laufen. Die Basisvektoren dieser ortsabhängigen und rechtwinkligen Koordinatensysteme lassen sich dabei direkt über die partiellen Ableitungen des Ortsvektors, gemäß der oben angegebenen Darstellung, nach den variablen Koordinaten $(r,φ)$ berechnen. Über die partiellen Ableitungen lassen sich auch die totalen Differentiale des Ortsvektors angeben:

$\mathrm{d}x=\frac{\partial x}{\partial r}\mathrm{d}r +\frac{\partial x}{\partial \phi}\mathrm{d}\phi = \cos \phi \,\mathrm{d}r - r\cdot\sin \phi \,\mathrm{d} \phi$

$\mathrm{d}y=\frac{\partial y}{\partial r}\mathrm{d}r +\frac{\partial y}{\partial \phi}\mathrm{d}\phi = \sin \phi \,\mathrm{d}r + r\cdot\cos \phi \,\mathrm{d} \phi$

Die Differentiale dx,dy,dr, $dφ$ werden auch als Koordinatendifferentiale bezeichnet. Bei diesem Beispiel haben die mit dem Differentialoperator „d“ verknüpften infinitesimalen Größen nicht immer die Bedeutung eines Abstandes. Man zeigt vielmehr relativ leicht, dass für die Abstände in radialer bzw. azimutaler Richtung gilt, dass zwar 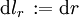$\mathrm dl_r\,:=\mathrm dr$ ist, aber 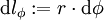$\mathrm dl_\phi :=r\cdot\mathrm d\phi$ ; d. h. 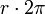erst mit dem Vorfaktor „ $r$ “ ergibt sich durch Integration über $dΦ$ von 0 bis $2π$ eine bekannte Größe der Dimension „Länge“, nämlich der Kreisumfang $r\cdot 2\pi$ .

Die Polarkoordinaten oder ihre dreidimensionale Verallgemeinerung, die Kugelkoordinaten, werden auch als krummlinig bezeichnet, da sie die Abstandberechnung auf einer gekrümmten Fläche, z. B. der Kugeloberfläche, ermöglichen. Es handelt sich – wie auch bei anderen Standardbeispielen, etwa den Zylinderkoordinaten, den elliptischen Koordinaten u.s.w. – um orthogonale krummlinige Koordinaten.

Ein wesentliches Hilfsmittel der klassischen Differentialgeometrie sind Koordinatentransformationen zwischen beliebigen Koordinaten, um geometrische Strukturen beschreiben zu können.

Die aus der Analysis bekannten, mit der Größe $\nabla$ gebildeten Differentialoperatoren können relativ leicht auf orthogonale krummlinige Differentialoperatoren erweitert werden. Z. B. gelten in allgemeinen orthogonalen krummlinigen Koordinaten bei Benutzung dreier Parameter 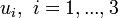$u_i,\,\,i=1,...,3$ und der zugehörigen Einheitsvektoren 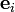$\mathbf e_i$ in Richtung von 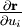$\tfrac{\partial\mathbf r}{\partial u_i}$ folgende Beziehungen mit Größen $a i$ , die nicht notwendig konstant sind, sondern von $u 1$ , $u 2$ und $u 3$ abhängen können:

$\begin{align} \mathrm d\mathbf r &amp;=\sum\limits_{i=1}^3{\rm d}l_i\mathbf e_i=\sum\limits_{i=1}^3\,a_i\,\mathrm du_i\,\mathbf e_i\\ {\rm d}V&amp;=a_1\mathrm du_1\cdot a_2\mathrm du_2\cdot a_3\mathrm du_3\\ \nabla^2 f&amp;=\frac{1}{a_1a_2a_3} \frac{\partial}{\partial u_1}\left(\frac{a_2a_3}{a_1}\frac{\partial f}{\partial u_1}\right)+ \cdots + \cdots \end{align}$

Dabei entstehen die durch Punkte angedeuteten zwei weiteren Terme aus dem ersten Term durch zyklische Vertauschung der Indizes. 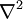$\nabla^2$ bezeichnet den Laplace-Operator. Er kann aus dem Skalar-wertigen div-Operator und dem Vektor-wertigen grad-Operator zusammengesetzt werden gemäß

$\nabla^2 f={\rm div\,\,(\,\,grad} \,f\,)$

wobei

$\begin{align} {\rm div\,\,}\mathbf v\,&amp;=\,\frac{1}{a_1a_2a_3}\frac{\partial (a_2a_3 v_1)}{\partial u_1}+ \cdots + \cdots\\ {\rm grad\,\,} f&amp;=\sum\limits_{i=1}^3\,\frac{1}{a_i}\frac{\partial f}{\partial u_i}\,\mathbf e_i \end{align}$

Die Formel für die Divergenz beruht auf der koordinatenunabhängigen Darstellung

${\rm div\,\,}\mathbf v\,=\,\lim_{\Delta V\to 0}\,\Big\{\frac{1}{|\Delta V|}\,\iint\limits_{\partial (\Delta V)} \mathbf v\cdot \mathbf n{\rm d}^{(2)}A\Big\}\,\,,$

wobei über die geschlossene, $Δ V$ berandende Fläche integriert wird. 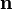$\mathbf n$ bezeichnet den zugehörigen äußere Normalenvektor, $d (2) A$ das zugehörige infinitesimale Flächenelement, 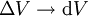$\Delta V \to {\rm d}V$ . Im allgemeinsten Fall – also für nicht-orthogonale, krummlinige Koordinaten – kann man diese Formel ebenfalls verwenden.

Kovariante Ableitung

Allgemeine, auf nicht notwendig orthogonalen krummlinigen Koordinaten beruhende Ableitungsoperatoren sind z. B. die kovarianten Ableitungen, die u. a. in Riemannschen Räumen verwendet werden, wo sie in spezifischer Weise vom „inneren Produkt“, d. h. von der sog. „metrischen Fundamentalform“ des Raumes, abhängen. In anderen Fällen sind sie aber unabhängig von der Existenz einer lokalen Metrik oder können sogar extern vorgegeben sein, z. B. in Mannigfaltigkeiten „mit Konnexion“.

Sie ermöglichen u. a. die Definition von Verbindungslinien in gekrümmten Räumen, z. B. die Definition von Geodäten im Riemannschen Raum. Geodätische Linien sind die lokal kürzesten Verbindungen zwischen zwei Punkten in diesen Räumen. Die Längenkreise auf einer Kugel sind Beispiele für geodätische Linien, nicht aber die Breitenkreise (Ausnahme: Äquator).

Mit Hilfe allgemeiner Koordinatentransformationen werden im Riemannschen Raum die Christoffelsymbole 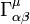$\Gamma^\mu_{\alpha\beta}$ definiert. Diese gehen, entsprechend der unten gegebenen Basisdefinition, explizit in die Berechnung der kovarianten Ableitung eines Vektorfeldes ein.

Die kovariante Ableitung ist eine Verallgemeinerung der partiellen Ableitung des flachen (euklidischen) Raumes für gekrümmte Räume. Im Gegensatz zur partiellen Ableitung erhält sie die Tensoreigenschaft; im euklidischen Raum reduziert sie sich zur partiellen Ableitung. Im gekrümmten Raum sind die kovarianten Ableitungen eines Vektorfeldes im Allgemeinen nicht miteinander vertauschbar, ihre Nichtvertauschbarkeit wird zur Definition des Riemann'schen Krümmungstensors verwendet.

Ein weiterer wichtiger Begriff im Zusammenhang mit gekrümmten Räumen ist die Parallelverschiebung. Die kovariante Ableitung der Komponenten eines Vektors ist bei Parallelverschiebung null. Trotzdem kann die Parallelverschiebung eines Vektors entlang einer geschlossenen Kurve im gekrümmten Raum dazu führen, dass sich der verschobene Vektor nicht mit seinem Ausgangsvektor deckt.

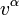Der zugehörige Formalismus beruht auf der Vorschrift, dass man Vektoren $\mathbf v$ als Summe $v^\alpha \mathbf e_\alpha$ schreibt, wobei sich u. U. (nämlich gerade bei obigem „Paralleltransport“) nicht die Komponenten $\,v^\alpha$ , sondern nur die Basiselemente 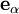$\mathbf e_\alpha$ ändern, und zwar nach der naheliegenden Regel: $d\mathbf e_\alpha=\Gamma_{\alpha \beta}^{\mu}dx^\beta\mathbf e_\mu$ . Kovariante und partielle Ableitung, meist mit Semikolon bzw. Komma geschrieben, sind also verschieden, und zwar gilt:

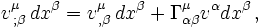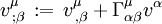$v^\mu_{\,;\beta}\,dx^\beta =v^\mu_{\,,\beta}\,dx^\beta+\Gamma^\mu_{\alpha \beta}v^\alpha dx^\beta\,,$ also $v^\mu_{\,;\beta} \,:=\,v^{\mu}_{\,,\beta}+\Gamma^\mu_{\alpha \beta}v^\alpha$ oder auch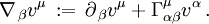 $\nabla_{\,\beta} v^\mu \,:=\,\partial_{\,\beta} v^\mu +\Gamma^\mu_{\alpha \beta}v^\alpha\,.$

In Mannigfaltigkeiten mit Zusatzstruktur (z. B. in riemannschen Mannigfaltigkeiten oder bei den sog. Eichtheorien) muss natürlich diese Struktur mit der Übertragung verträglich sein. Das ergibt Zusatzbeziehungen für die Christoffelsymbole. Z. B. dürfen sich bei riemannschen Räumen die Abstands- und Winkelverhältnisse zweier Vektoren bei Parallelverschiebung nicht ändern, und die Christoffelsymbole berechnen sich demzufolge in bestimmter Weise allein aus der metrischen Struktur.

Krümmungstensor

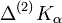Die oben erwähnte Raumkrümmung ergibt sich analog: Wenn man den Basisvektor $\mathbf e_\alpha$ im mathematisch positivem Sinn (entgegengesetzt zum Uhrzeigersinn) erst eine infinitesimale Strecke $d x β$ in $β$ -Richtung und anschließend eine infinitesimale Strecke $d x γ$ in $γ$ -Richtung verschiebt, erhält man ein Ergebnis, das wir in der Form $\tfrac{1}{2}\Delta^{(2)} K_\alpha$ schreiben können. Bei Vertauschung der Reihenfolge, also bei entgegengesetztem Drehsinn, erhält man das entgegengesetzte Ergebnis. Die Differenz $\,\Delta^{(2)} K_\alpha$ lässt sich also mit einer Größe 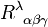$R^\lambda_{\;\; \alpha \beta \gamma}$ , die sich aus den Christoffelsymbolen ergibt, in folgender Form schreiben:

$\begin{align} \Delta^{(2)} K_\alpha &amp;= R^\lambda_{\;\;\alpha \beta \gamma}{\rm d}x^\beta \,{\rm d}x^{\gamma \,}\mathbf e_\lambda\\ &amp;\equiv\,(\Gamma^\mu_{\alpha \beta}\,\Gamma^\lambda_{\mu \gamma}-\Gamma^\mu_{\alpha\gamma}\Gamma^\lambda_{\mu\beta}+\partial_\gamma\Gamma^\lambda_{\alpha\beta}-\partial_\beta\Gamma^\lambda_{\gamma \alpha}\,)\,{\rm d}x^\beta \,{\rm d}x^{\gamma\,}\,\mathbf e_\lambda \end{align}$

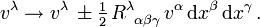Bei Parallelverschiebung des Vektors $\mathbf v$ ergibt sich entsprechend: $v^\lambda\to v^\lambda \,\pm \tfrac{1}{2}\,R^\lambda _{\;\; \alpha \beta \gamma}\,v^\alpha \,{\rm d}x^\beta \,{\rm d}x^\gamma \,.$ Die Komponenten 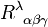$R^\lambda _{\;\; \alpha \beta \gamma}$ bilden den Krümmungstensor.